SWUST OJ#794 最近对问题

青衿白首志

已于 2022-11-06 22:13:28 修改

阅读量2.5k

点赞数 12

分类专栏：数据结构系列（对应swust oj题解）（持续更新中）文章标签：算法人工智能 c++

于 2022-09-14 13:22:53 首次发布

本文链接：https://blog.csdn.net/qq_62102968/article/details/126845886

版权

数据结构系列（对应swust oj题解）（持续更新中）专栏收录该内容

41 篇文章 17 订阅

订阅专栏

题目

思路

方法1：暴力 O(n²）

方法2：换系暴力（玄学AC 复杂度O(n) ）

题目

题目描述

设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S，设计算法找出集合S中距离最近的点对。

输入

多组测试数据，第一行为测试数据组数n（0<n≤100），每组测试数据由两个部分构成，第一部分为一个点的个数m（0<m≤1000），紧接着是m行，每行为一个点的坐标x和y，用空格隔开，（0<x，y≤100000）

输出

每组测试数据输出一行，为该组数据最近点的距离，保留4为小数。

样例输入
2
2
0 0
0 1
3
0 0
1 1
1 0
样例输出
1.0000
1.0000

思路

首先，用结构体构造点集 (或者stl的pair也行）

#define N 100005
typedef struct {
    double x,y;
}point;
point p[N];

方法1：暴力 O(n²）

暴力法：即枚举所有的两个点，依次算距离比较得出最小值。

double ans=9999999;
for(int i=1;i<n;i++) {
    for(int j=i+1;j<=n;j++) {
        ans=min(ans,sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y)));
    }
}

方法2：换系暴力（玄学AC 复杂度O(n) ）

此方法可能存在一定误差

换系暴力法：时间复杂度O(n) 但实际测试由于排序应该是O(nlogn)

也就是说，重新建系，重新做一个x'轴和y'轴，然后在新的坐标轴内重新对点按照新坐标从小到大排序，然后再进行暴力搜索，这时候由于已经排好序，不需要全部搜完，只需要搜5个就行，所以为O(n)的复杂度。

以下为证明为什么重新建系后重排就只需搜5个：

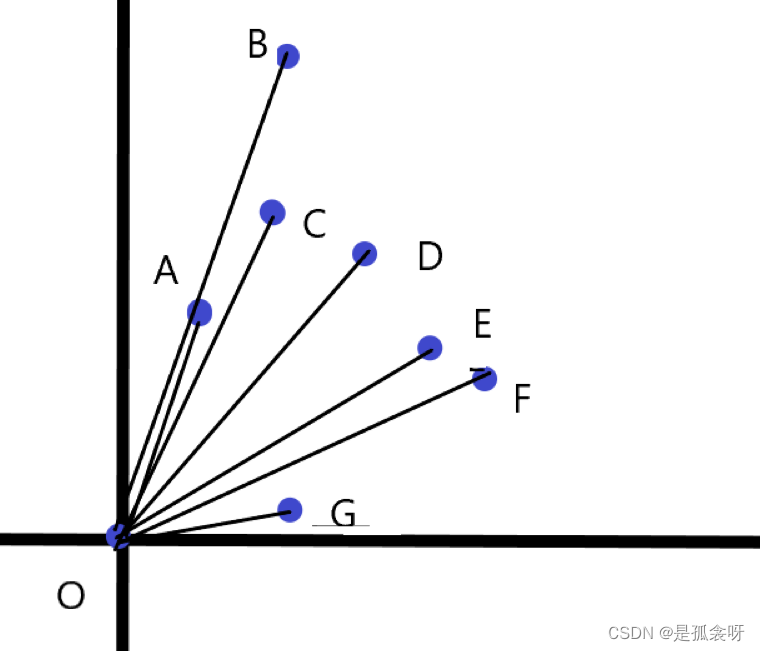
重新建立新的坐标轴，在新的坐标中，我们可以发现点的顺序相比原来发生了改变。

原先是OABCGDEF 现在是BACDOEGF。

现在在新的顺序再进行暴力搜索，那么就只需要搜索每个点与往后5个点的距离再比较大小即可

即：只需要求出BA BC BD BO BE AC AD AO AE AF CD CO CE CF CG DO DE DF DG OE OF OG EF EG FG 。最终结果一定再这里面，就不需要全部都搜索。在原来是要搜n(n-1）次，现在只需（5n-10）次，就大大的降低了复杂度。

注意：重新建系还是有可能存在最近两个点并非相距5之内，由于建系有无数种，再重新建系即可，总有一次可AC。

根据数学计算，重新建系假设旋转是Θ度，那么新的坐标为：

x ' =x*cosΘ - y*sinΘ

y ' =x*sinΘ + y*cosΘ

以下为证明过程（不需要可跳过）

理论上推出新坐标后，对新坐标排序

//根据新坐标排序
bool cmp(point i,point j) {
    return i.xx<j.xx;
}

for(int i=1;i<=n;i++) {
    cin>>p[i].x>>p[i].y;
    p[i].xx=p[i].x*cos(1)-p[i].y*sin(1); 
    //假设旋转1弧度(57度) 求出新坐标,排序与y没啥关系,就不求yy
}
sort(p+1,p+n+1,cmp);

在新坐标排序后直接暴力搜5个即可

double distance(int i,int j) {
    return sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
}

//暴力往后每次都枚举5个 看似O(n²)实则O(n)
double ans=99999999;
for(int i=1;i<=n;i++) {
for(int j=1;j<=5&&j+i<=n;j++) {
        ans=min(ans,distance(i,i+j));
    }
}

方法3：分治 O(nlogn)

首先由于输入的点是乱的，所以我们必须按照坐标从小到大进行排序。

//对点集排序
bool cmp1(point a,point b) {
    if(a.x==b.x) {
        return a.y<b.y;
    }
    else return a.x<b.x;
}

由于暴力枚举实在太多，我们采用二分，把原来的点集分成左右两部分，并求出左右两边最小的距离，然后总的最小距离：dis=min(disleft，disright）

你问左右两边最小距离的dis怎么求？那重复此过程，左右两边再次砍成两半呀。

一直重复下去，可在O (logn) 的复杂度内求出最小的dis

//left,right代表是第几个点
double merge(int left,int right) {
    if(left==right) return 99999999; //表示同一个点,直接返回一个无效值
    if(left+1==right) {
        return distance(left,right); //两个点挨着,那就返回他们的距离
    }
    double dis1=merge(left,mid);
    double dis2=merge(mid+1,right);
    double dis=min(dis1,dis2); //求出最小dis
    return dis; 
}

但是，我们的前提是点全在一边，如果说最终的dis，一个点在左，一个点在右边，那该怎么办呢？

采用反证法，先假设存在这种情况，然后我们在中轴线上每个点都画圆进行等距处理，半径为dis。

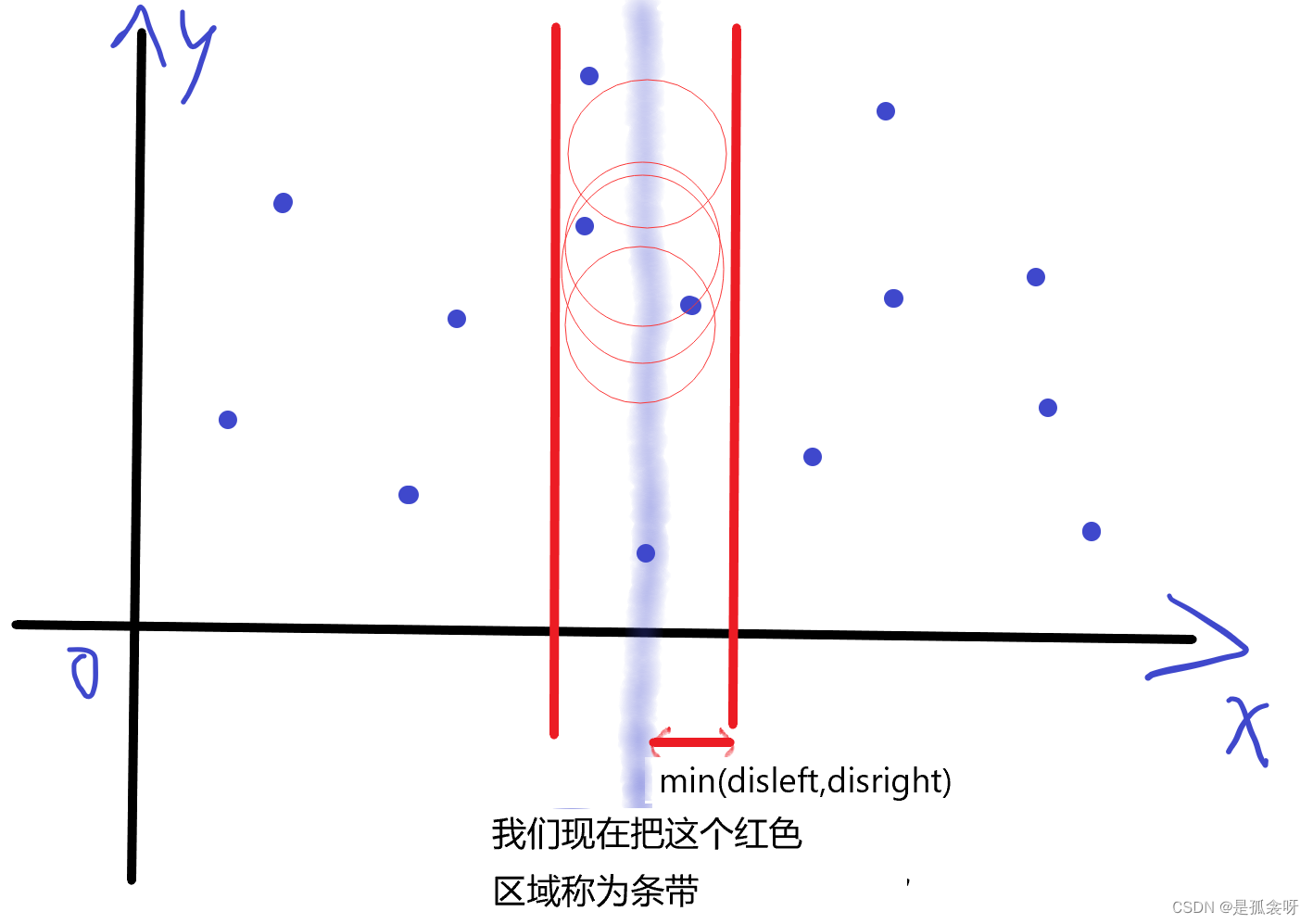
画出来实际上是一个长方形。

考虑穿过中轴线，查找 x 坐标比 dis 更接近中轴线的所有点。即fabs（p[x] - p[mid] <= dis ) （fabs函数表示浮点数绝对值）

把这些点存入条带中。

//sum动态计算条带中点的个数
int sum=0; 
for(int i=left;i<=right;i++) {
    if(fabs(p[i].x-p[mid].x)<=dis) {
        tiaodai[++sum]=i;
    }
}

由于此时条带也是乱序，加上是竖着的，所以我们再次按照y从小到大排序。

bool cmp2(int a,int b) {
    return p[a].y<p[b].y;
}

//对条带排序
    sort(tiaodai+1,tiaodai+sum+1,cmp2);

然后再次暴力搜索找到最小值，虽然这次还是O(n²），但基数相比刚才少太多太多了。

for(int i=1;i<=sum;i++) {
    for(int j=i+1;j<=sum;j++) {
        dis=min(dis,distance(tiaodai[i],tiaodai[j]));
    }
}

代码

玄学AC法

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#define endl '\n'
#define N 200005
typedef long long ll;
using namespace std;
typedef struct {
    double x,y; //原坐标
    double xx,yy; //新坐标
}point;
point p[N]; 
//计算距离
double distance(int i,int j) {
    return sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
}
//根据新坐标排序
bool cmp(point i,point j) {
    return i.xx<j.xx;
}
int main() {
    int t;cin>>t;
    while(t--) {
        int n;cin>>n;
        for(int i=1;i<=n;i++) {
            cin>>p[i].x>>p[i].y;
            p[i].xx=p[i].x*cos(1)-p[i].y*sin(1); 
            //假设旋转1弧度(57度) 求出新坐标,排序与y没啥关系,就不求yy
        }
        sort(p+1,p+n+1,cmp);
        //暴力往后每次都枚举5个 看似O(n²)实则O(n)
        double ans=99999999;
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=5&&j+i<=n;j++) {
                ans=min(ans,distance(i,i+j));
            }
        }
        printf("%.4lf\n",ans);
    }
    return 0;
}

正常分治法

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <time.h>
#define endl '\n'
#define N 200005
typedef long long ll;
using namespace std;
typedef struct {
    double x,y;
}point;
point p[N];
int tiaodai[N];
//对点集排序
bool cmp1(point a,point b) {
    if(a.x==b.x) {
        return a.y<b.y;
    }
    else return a.x<b.x;
}
bool cmp2(int a,int b) {
    return p[a].y<p[b].y;
}
double distance(int i,int j) {
    return sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
}
double merge(int left,int right) {
    //递归找出左右两边的dis
    double dis=999999;
    if(left==right) return dis;
    if(left+1==right) {
        return distance(left,right);
    }
    int mid=(left+right)>>1;
    double dis1=merge(left,mid);
    double dis2=merge(mid+1,right);
    dis=min(dis1,dis2);
    //sum动态计算条带中点的个数
    int sum=0; 
    for(int i=left;i<=right;i++) {
        if(fabs(p[i].x-p[mid].x)<=dis) {
            tiaodai[++sum]=i;
        }
    }
    //对条带排序
    sort(tiaodai+1,tiaodai+sum+1,cmp2);
    //暴力搜索结果 复杂度O(n²) 此处也可以再次优化
    //虽然还是O(n²) 但n的基数相比最先少太多太多了
    //所以总时间复杂度O(nlogn²)=O(2nlogn) 即O(nlogn) 
    for(int i=1;i<=sum;i++) {
        for(int j=i+1;j<=sum;j++) {
            dis=min(dis,distance(tiaodai[i],tiaodai[j]));
        }
    }
    return dis;
}
int main() {
    int t;cin>>t;
    while(t--) {
        int n;cin>>n;
        for(int i=1;i<=n;i++) {
            cin>>p[i].x>>p[i].y;
        }
        sort(p+1,p+n+1,cmp1);
        printf("%.4lf\n",merge(1,n));
    }
    return 0;
}

青衿白首志

关注

12
点赞
踩
30

收藏

觉得还不错? 一键收藏
打赏
1
评论
SWUST OJ#794 最近对问题

题目描述设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S，设计算法找出集合S中距离最近的点对。输入多组测试数据，第一行为测试数据组数n（0
复制链接

扫一扫