目录
一、概念
松弛变量 剩余变量
1.1整数规划的定义:
数学规划中的变量(部分或者全部)限制为整数的时候,称为整数规划。
整数规划的分类:
如果不加特殊说明,指的就是整数线性规划(在线性规划的模型中变量限制为整数)。分为两类:
1:变量全部限制为整数,称纯整数规划。
2:变量部分限制为整数,称混合整数规划。
整数规划的特点:
1:原线性规划的最优解全是整数,则自变量限制为整数之后,最优解不变。
2:整数规划没有可行解。
0-1型整数规划
顾名思义,在该模型下,变量xi的值只能取到0或者1,称xi为0-1变量或者二进制变量。可由约束条件 0 <= xi <= 1而且xi为整数所代替。
在一些互相排斥的约束问题:比如两种方式可供选择,但是只能选择一种的情形。
在一些指派问题的数学模型中:比如:n个人分配去做n项工作,每个人都做且都只能做一项工作。
1.2关系

又不理解了吧,没关系上题
1.3例题
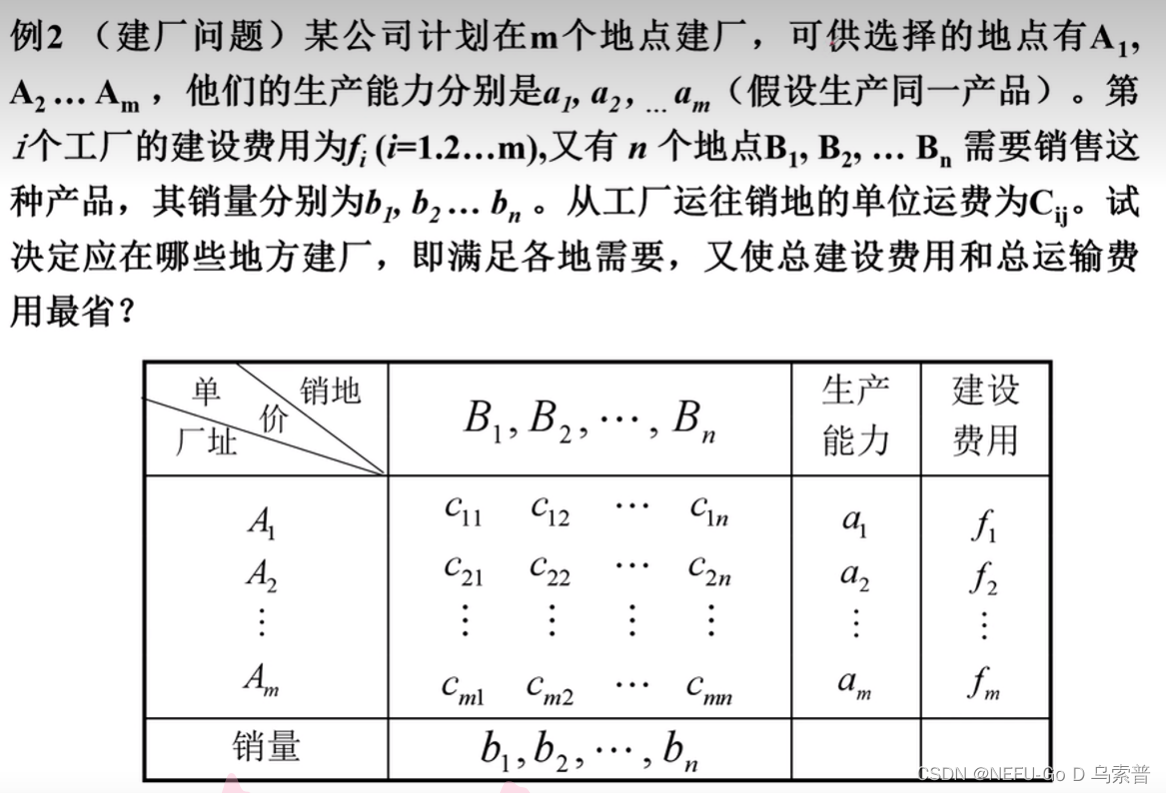

应用于运输问题、指派问题
1.4方法
i)分枝定界法—可求纯或混合整数线性规划。
(ii)割平面法—可求纯或混合整数线性规划。
(iii)隐枚举法—求解“0-1”整数规划:
①过滤隐枚举法;
②分枝隐枚举法。
(iv)匈牙利法—解决指派问题(“0-1”规划特殊情形)。
(v)蒙特卡洛法—求解各种类型规划。
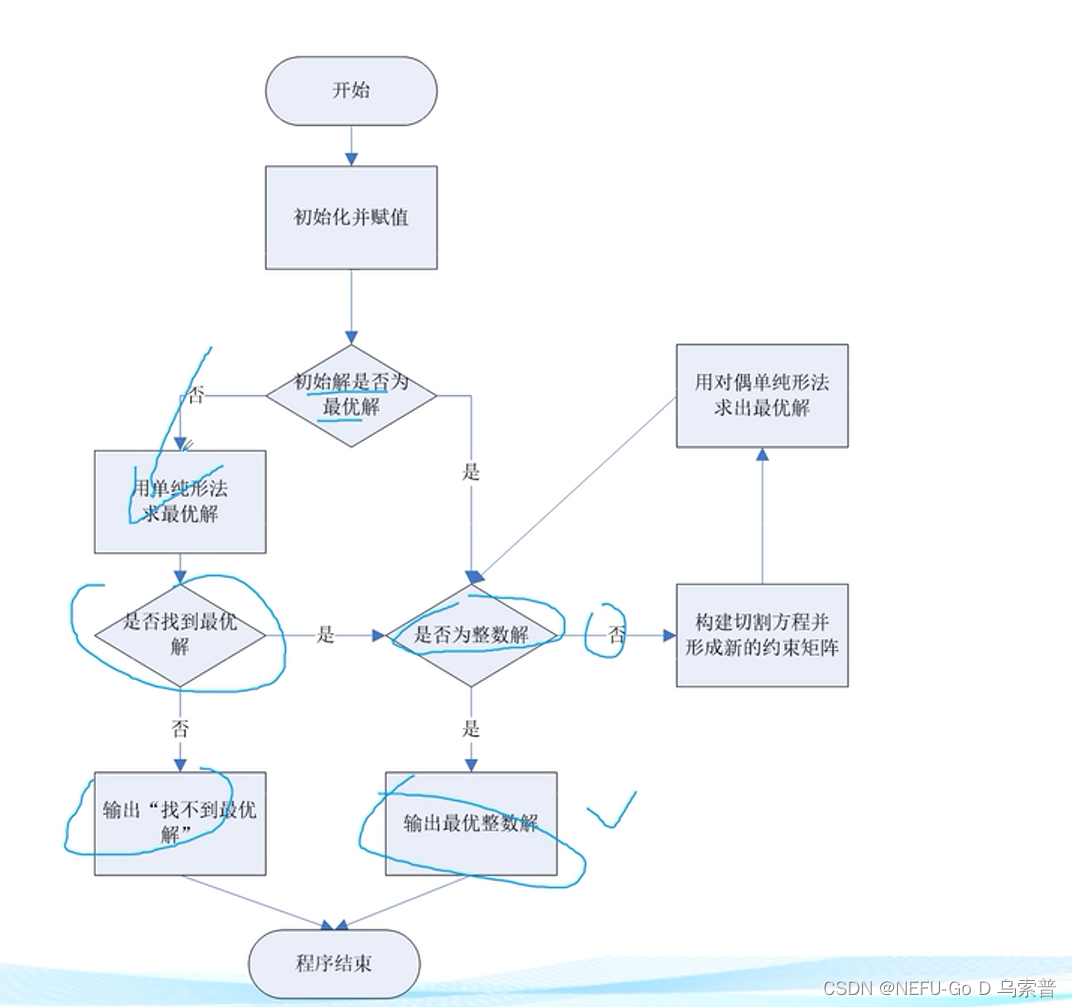
二、分枝定界法
- 分枝定界法适用于求解完全整数规划与混合整数规划,混合整数规划相比较而言更加简单,只需要针对非限定为整数的变量不分枝即可。
- 我们首先来了解一下分枝定界法中三个基本操作的含义。分枝:将全部可行解空间分割为越来越小的子集;定界:对于分枝后的每一个子集计算目标函数值得上界与下界;剪枝:根据上下界忽略掉超出界限得部分可行解。下面我们首先通过一个例题,以手写算法得方式来感受一下算法过程。
上题

总结来说,分枝定界法多次计算线性规划,缩小搜索范围,逼近整数规划的最优解。针对线性规划问题我们已经有了高效便捷的算法,因此多次计算线性规划问题解决整数规划问题同样具有效率
python代码失败
import math
from scipy.optimize import linprog
import sys
def integerPro(c, A, b, Aeq, beq,t=1.0E-12):
# 求解松弛问题
res = linprog(c, A_ub=A, b_ub=b, A_eq=Aeq, b_eq=beq)
bestVal = sys.maxsize
bestX = res.x
if not(type(res.x) is float or res.status != 0):
bestVal = sum([x*y for x,y in zip(c, bestX)])
# 停止条件 & bound
if all((int((x-math.floor(x)))<t or int((math.ceil(x)-x)<t)) for x in bestX):
return (bestVal,bestX)
else:
# 进行branch,这里简单选择第一个非整数变量
ind = [i for i, x in enumerate(bestX) if (x-math.floor(x))>t and (math.ceil(x)-x)>t][0]
# branch出两个子问题
newCon1 = [0]*len(A[0])
newCon2 = [0]*len(A[0])
newCon1[ind] = -1
newCon2[ind] = 1
newA1 = A.copy()
newA2 = A.copy()
newA1.append(newCon1)
newA2.append(newCon2)
newB1 = b.copy()
newB2 = b.copy()
newB1.append(-math.ceil(bestX[ind]))
newB2.append(math.floor(bestX[ind]))
r1 = integerPro(c, newA1, newB1, Aeq, beq)
r2 = integerPro(c, newA2, newB2, Aeq, beq)
# tree search,这里使用width first
if r1[0] < r2[0]:
return r1
else:
return r2
c = [-5,-8]
A = [[1,1],[5,9]]
b = [6,45]
Aeq = [[0,0]]
beq = [0]
print(integerPro(c, A, b, Aeq, beq))
- Lingo代码如下:
-
model: max=5*x1+8*x2; x1+x2<6; 5*x1+9*x2<45; @gin(x1); @gin(x2); end
三、割平面法
基本思想:
1.如果松弛问题(P0)无解,则(P)无解;
2.如果(P0)的最优解为整数向量,则也是(P)的最优解;
3.如果(P0)的解含有非整数分量,则对(P0)增加割平面条件:即对(P0)增加一个线性约束,将(P0)的可行域割掉一块,使得非整数解恰好在割掉的一块中,但又没有割掉原问题(P)的可行解,得到问题(P1),重复上述的过程。
上例题

基于cvxpy下的线性规划
import cvxpy as cp
import numpy as np
# 不懂见数学原型中的定义, 什么价值向量资源向量什么的
c = np.array([3,1,3])
a = np.array([[-1,2,1],[0,4,-3],[1,-3,2]])
b = np.array([4,2,3])
######
x = cp.Variable(3) # 用cvxpy来定义两个整数决策变量, 也就是约束x为整数
obj = cp.Maximize(c*x) # 目标函数
cons = [a * x <= b, x >= 0] # 约束条件
prob = cp.Problem(obj, cons) # 构建问题模型
prob.solve(solver='GLPK_MI', verbose=True) # 求解
print("最优值", prob.value)
print("最优解", x.value)
基于cvxpy下的整数规划
#导入numpy
import numpy as np
#导入numpy
import cvxpy as cp
#设置目标函数中变量个数
n=3
#输入目标函数的系数
c=np.array([3,1,3])
#输入约束条件的系数矩阵(3×3)
a=np.array([[-1,2,1],[0,4,-3],[1,-3,2]])
#输入b值(3×1)
b=np.array([4,2,3])
#创建x,个数是3
x=cp.Variable(n,integer=True)
#明确目标函数(此时c是3×1,x是3×1,但python里面可以相乘)
objective=cp.Maximize(cp.sum(c*x))
#明确约束条件,其中a是3×3,x是3×1,a*x=b(b为3×1的矩阵)
constriants=[0<=x,a*x<=b]
#求解问题
prob=cp.Problem(objective,constriants)
#这里solver必须使用cp.CPLEX,否则计算不出来,而CPLEX需要pip intall CPLEX(建议使用清华镜像)
resluts=prob.solve(solver=cp.CPLEX)
#输入结果
print(prob.value)#目标函数的值
print(x.value)#各x的值
基于Matlab的实现
函数原型
[x, fval] = intlinprog(c, intcon, A, b, Aeq, beq, lb, ub)
基本上和 linprog() 一样, intcon参数就是指定哪些变量有整数约束

例题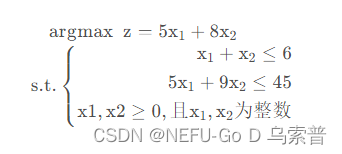
c = [-5; -8];
% 无论线性规划还是整数规划, 在matlab中默认都是求最小值,
% 题目要求最大值, 所以加个负号
A = [1, 1;
5, 9];
b = [6; 45];
lb = zeros(2, 1);
intcon = [1, 2];
% 着重看上面这个, 这里指定了x1, x2为整数
% 所以根据4.1.2数学原型中写到的intcon的意义, intcon = [1, 2]
[x, fval] = intlinprog(c, intcon, A, b, [], [], lb, []);
x
-fval % 因为之前为了求最大值加了负号, 所以这里再把答案负回来
四、0-1整数规划
指派问题

4.1匈牙利算法

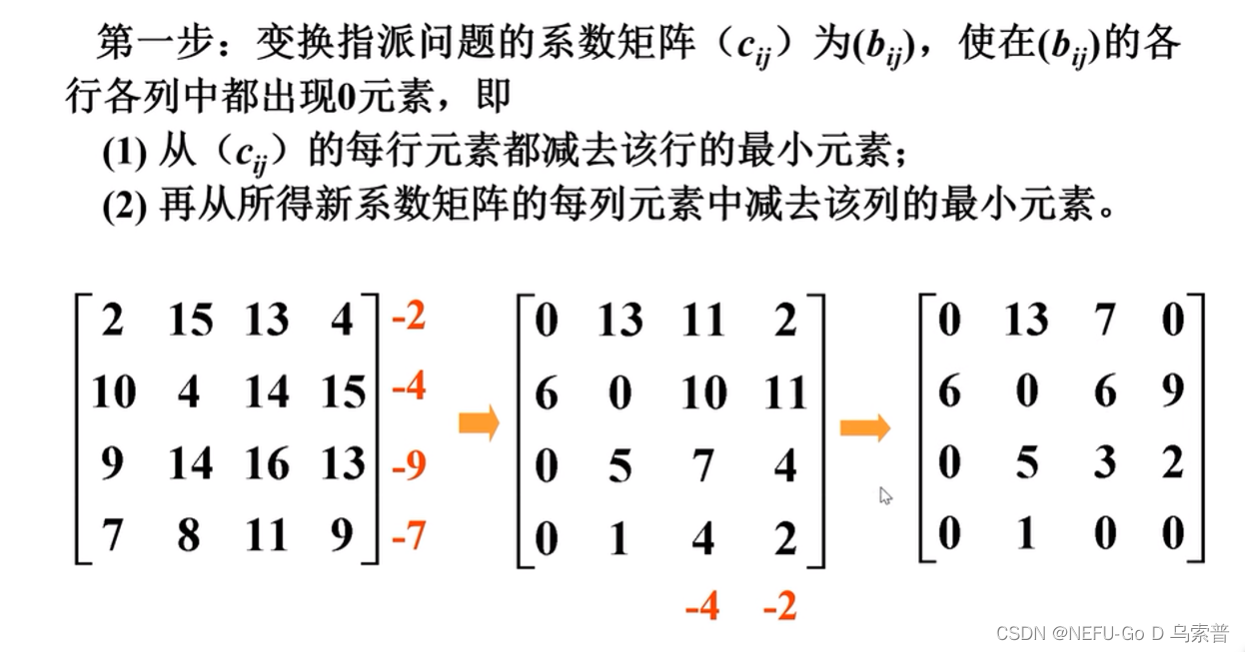

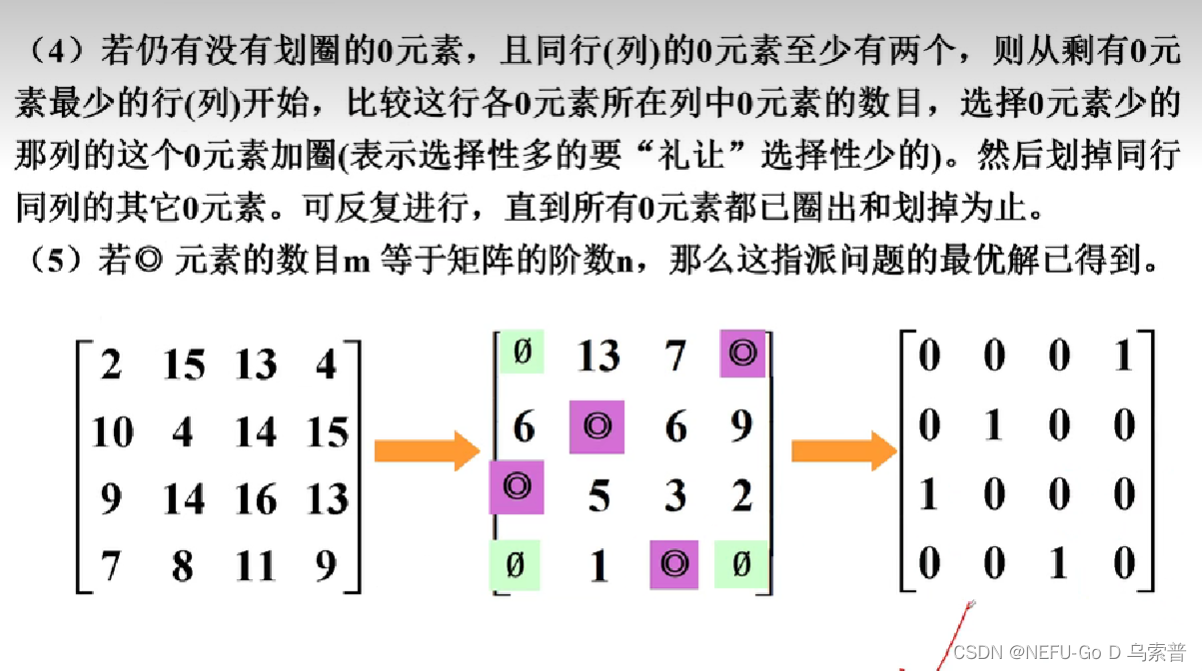

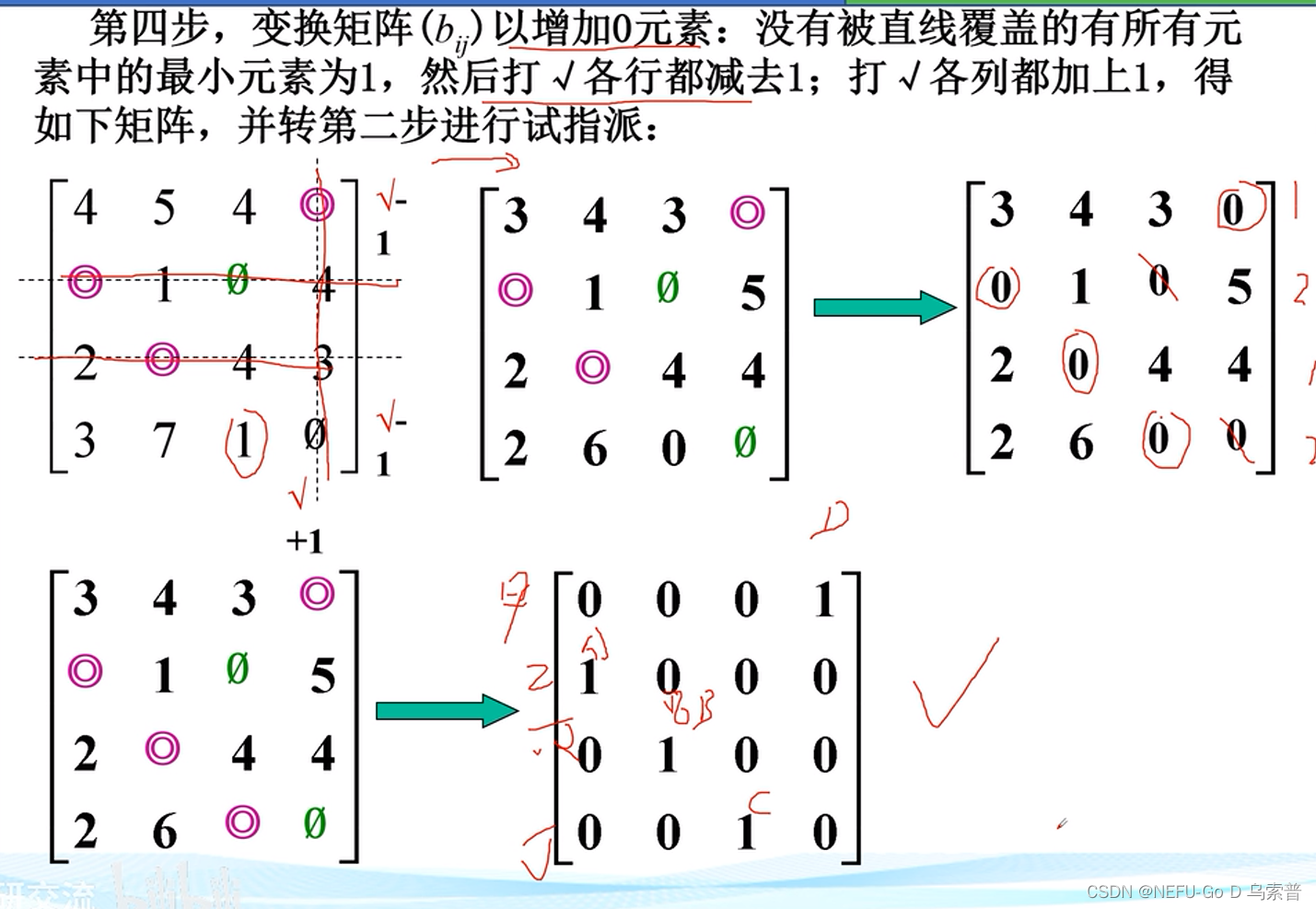
Matlab解法
c=[3,8,2,10,3;8,7,2,9,7;6,4,2,7,5;8,4,2,3,5;9,10,6,9,10];
c=c(:); %把矩阵c转换成向量
a=zeros(10,25); %10个方程(行+列),25个未知数
for i=1:5
a(i,(i-1)*5+1:5*i)=1;
a(5+i,i:5:25)=1;
end %此循环把指派问题转化为线性规划问题
b=ones(10,1);
[x,y]=linprog(c,[],[],a,b,zeros(25,1),ones(25,1));
X=reshape(x,5,5) %重构成矩阵
opt=y
python解法
from scipy.optimize import linear_sum_assignment
cost =np.array([[3,8,2,10,3],[8,7,2,9,7],[6,4,2,7,5],[8,4,2,3,5],[9,10,6,9,10]])
row_ind,col_ind=linear_sum_assignment(cost)
print(row_ind)#开销矩阵对应的行索引
print(col_ind)#对应行索引的最优指派的列索引
print(cost[row_ind,col_ind])#提取每个行索引的最优指派列索引所在的元素,形成数组
print(cost[row_ind,col_ind].sum())#数组求和
4.2过滤隐枚举法
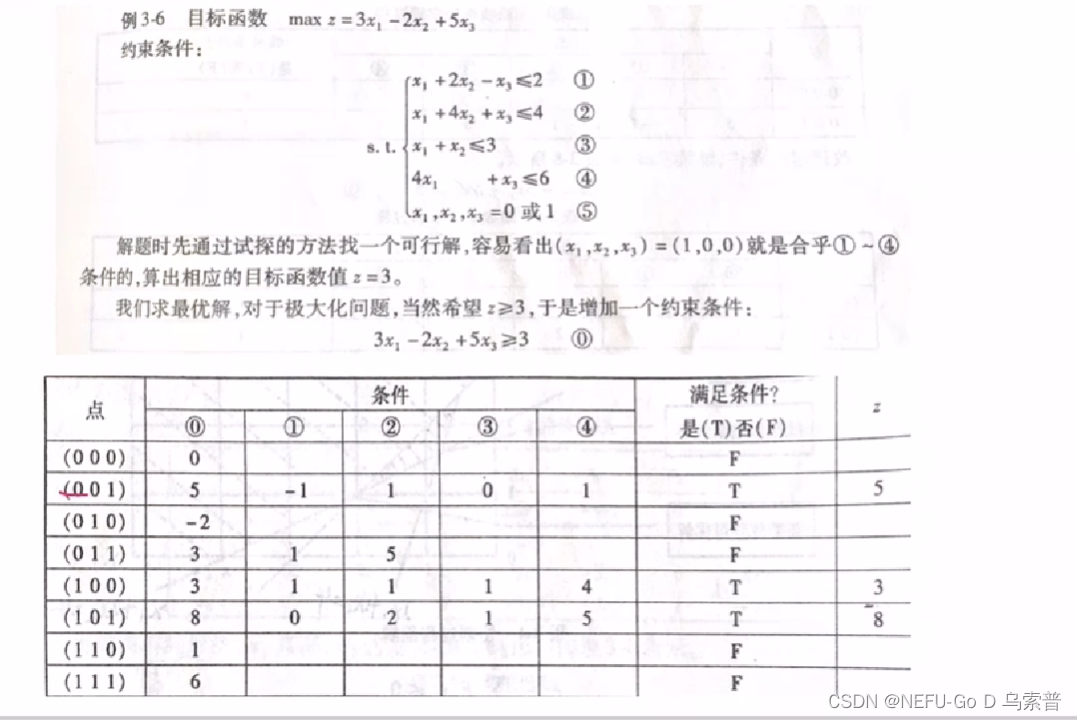
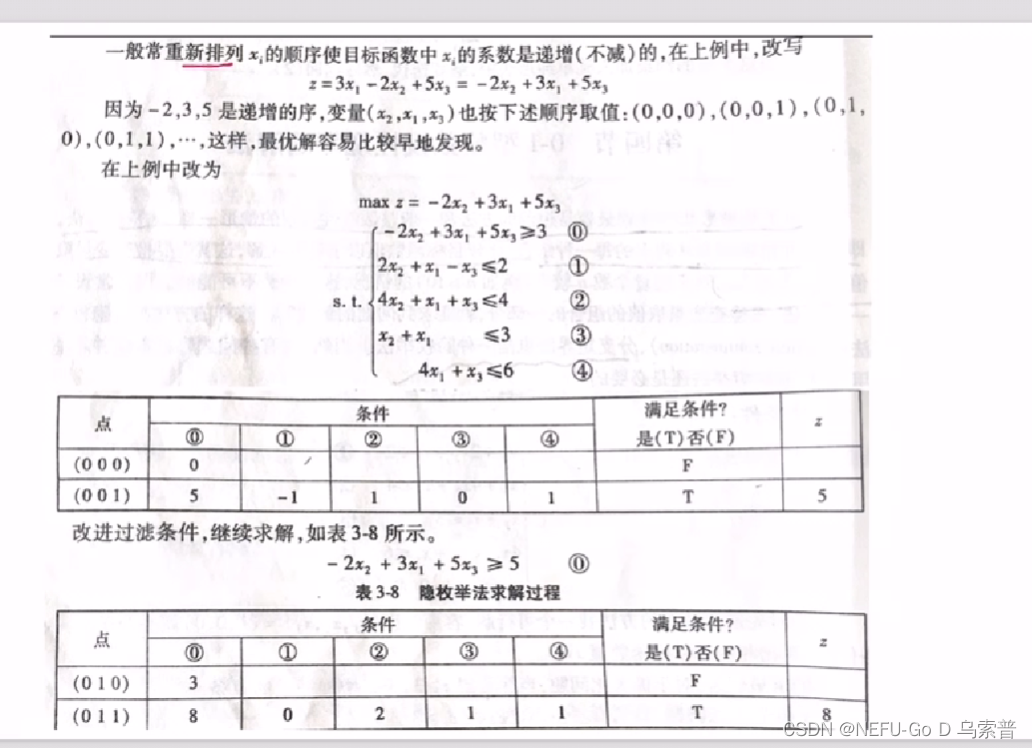
4.3蒙特卡洛随机取样法求解
先给出一个例子:
y = x^2, y = 12 - x与x轴在第一象限围成一个曲边三角形,设计一个随机试验求该图形的面积。
分析:可以在一个已知矩形面积(包含所求的曲边三角形)的矩形中生成n个随机数之后统计落在去边三角形中的随机数的个数,之后计算比值,从而得出面积。
clc
clear
x = unifrnd(0, 12, [1, 100000]);
y = unifrnd(0, 9, [1, 100000]);
ps = sum(y < x .^ 2 & x <= 3) + sum(y < 12 - x & x >= 3)
area = ps/100000 * 9 * 12
整数线性规划的计算机求解

在Matlab中求解混合整数线性规划的命令为
[x, fval] = intlinprog(f, intcon, a, b, aeq, beq, lb, ub)
% f, x, intcon, beq, lb, ub为列向量;a, aeq为矩阵。
例题
Matlab解法
clc
clear
f = [-3;-2;-1]
intcon = 3
a = ones(1,3)
b = 7
aeq = [4 2 1]
beq = 12
lb = zeros(3,1)
ub = [inf;inf;1]
x = intlinprog(f, intcon, a, b, aeq, beq, lb, ub)
% 求得最优解为x1 = 0, x2 = 5.5, x3 = 1; 目标函数的最优值为 z = -12。
例:
对于非线性整数规划,可使用蒙特卡洛法进行估算:
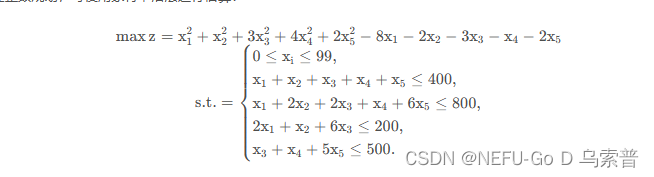
python解法:速度超级慢
import numpy as np
def check(x):
if x.sum() > 400:
return False
if x[0]+2*x[1]+2*x[2]+x[3]+6*x[4] > 800:
return False
if 2*x[0]+x[1]+6*x[2]>200:
return False
if x[2]+x[3]+5*x[3]>200:
return False
return True
def get_radom():
x = np.random.randint(100, size=5)
while not check(x):
x = get_radom()
return x
lim = 10**6
ans = -1
for i in range(lim):
num = get_radom()
ans = max(ans, num.all())
if i % 10000 == 0:
print(i)
print('ans=' + ans)























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










