C Looooops or Party

最新推荐文章于 2025-11-25 10:31:53 发布

原创最新推荐文章于 2025-11-25 10:31:53 发布 · 117 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法

本文解析了扩展欧几里得算法的应用及最小公倍数的计算方法，提供了具体的代码实现。

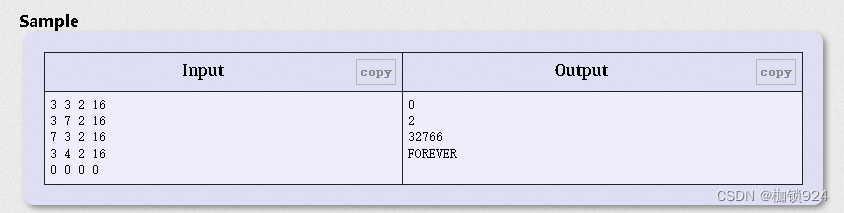
题目如上图

由题意可知

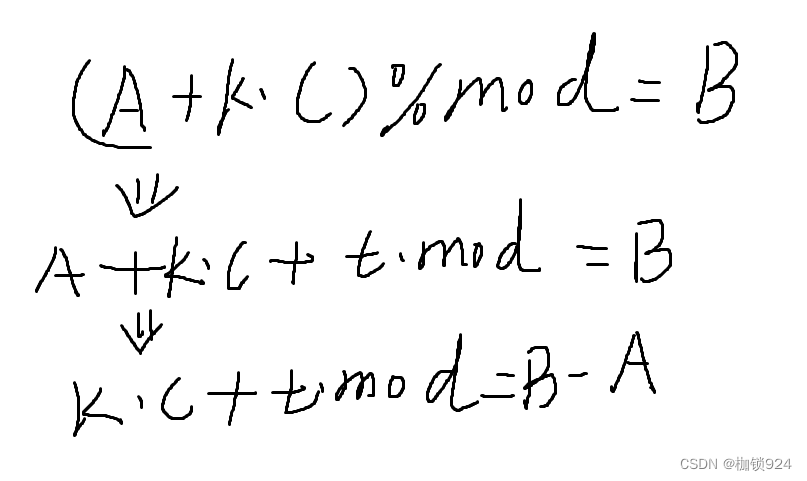
显然这是一个扩展欧几里得

那么我们另k为x，t为y，C为a，mod为b，B-A为c。

这样就出现了这样的式子：

ax+by=c，显然是扩展欧几里得的式子。

那么接下来就直接求解。

#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
#define N 100005
int a[N];
int T;
ll gcd(ll a,ll b){
	return b == 0 ? a : gcd(b,a%b);
}
ll edgcd(ll a,ll b,ll &x,ll &y){
	if(b == 0){
		x = 1;
		y = 0;
		return a;
	}
	ll res = edgcd(b,a%b,x,y);
	ll tmp = x;
	x = y;
	y = tmp - a/b*y;
	return res;
} 
void sol() {
    while(true){
    	ll a,b,c,k;
    	ll x1 = 0,y1 = 0;
    	cin >> a >> b >> c >> k;
    	if(!a && !b && !c && !k) break;
    	ll mod = (ll)1 << k;
    	ll A = c,B = mod,C = b-a;
    	if(C < 0) C += mod;
    	ll d = edgcd(A,B,x1,y1);
    	if(C%d != 0){
    		cout << "FOREVER\n";
    		continue;
		}
    	ll tmp1 = C/d;
    	x1 = (x1 * tmp1) % mod;
    	ll tmp = B/d;
    	x1 = (x1 % tmp + tmp) % tmp;
    	cout << x1 << '\n';
	}
}
int main() {
    ios::sync_with_stdio(false);
    sol();
	//if(!res) cout << "Impossible\n";
	//else cout << res << '\n'; 
    return 0;
}

然后就是另一题，题目如下

这道题的题意大致为让你求这些数的最小公倍数，然后保证任何一支队伍第一个来都能整除，如果超过1000000就输出“Too much money to pay!”。

知道求最小公倍数了显然就比较简单。

lcm(a,b)=(a*b)/gcd(a,b)。

然后按照这个公式算，就可以写代码了。

#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
#define N 100005
int a[N];
int T;
ll gcd(ll a,ll b){
	return b == 0 ? a : gcd(b,a%b);
}
void sol() {
    while(true){
    	int n;
    	cin >> n;
    	if(!n) break;
    	for(int i = 0;i < n;i++) cin >> a[i];
    	int res = 1;
    	bool ju = false;
    	for(int i = 0;i < n;i++){
    		res = res*a[i]/gcd(res,a[i]);
    		if(res >= 1000000){
    			ju = true;
    			break;
			}
		}
		if(ju) cout << "Too much money to pay!\n";
		else cout << "The CEO must bring " << res << " pounds.\n";
	}
}
int main() {
    ios::sync_with_stdio(false);
    sol();
    return 0;
}