【完全背包问题——附例题剖析】

完全背包

一、题目：

有 n(n ≤ 100) 种物品和一个容量为 m(m ≤ 10000) 的背包。第 i 种物品的容量是 c[i]，价值是 w[i]。现在需要选择一些物品放入背包，每种物品可以无限选择，并且总容量不能超过背包容 量，求能够达到的物品的最大总价值。

以上就是完全背包问题的完整描述，和 0/1 背包的区别就是每种物品可以无限选取；

1、状态设计

状态 (i, j) 表示前 i 种物品恰好放入容量为 j 的背包 (0 ≤ i < n，0 ≤ j ≤ m)；

令 dp[i][j] 表示状态 (i, j) 下该背包得到的最大价值，即前 i 种物品（每种物品可以选择无限 件）恰好放入容量为 j 的背包所得到的最大总价值；

2. 状态转移方程

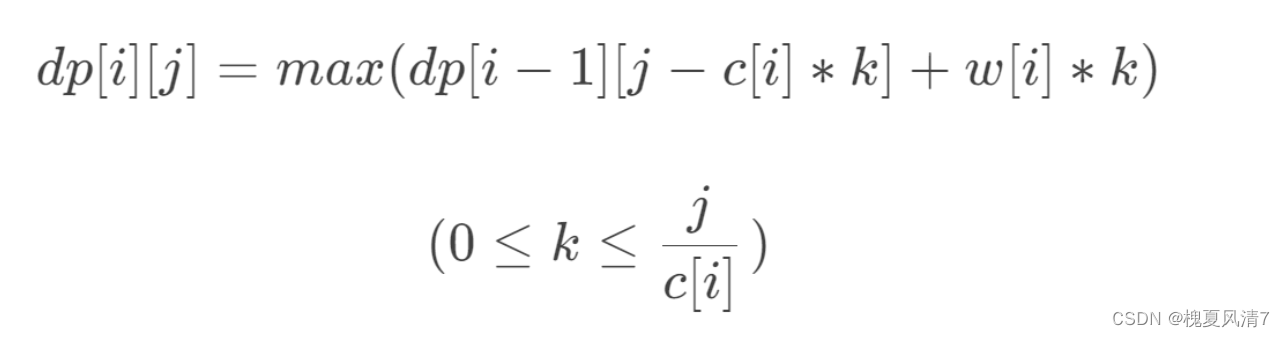
对于第 i 个物品有两种选择： 放 或 不放。

1 不放

​ 第 i 个物品不放入容量为 j 的背包，则问题转变为 “ 前 i - 1 个物品放入容量为 j 的背包 ” ，则

dp[i][j] = dp[i-1][j];

2 放

第 i 个物品放入k件到容量为 j 的背包, 则问题转变为 “ 前 i - 1 个物品放入容量为 j - k * c[i] 的背包 ”，则此时的最大价值就是 “ 前 i - 1 个物品放入 容量为 j - k * c[i] 的背包 ” 的最大价值 加上 k件第 i 个物品的最大价值，即

dp[i][j] = dp[i-1][j- k * c[i]] + K * w[i];

枚举出 k 的所有取值对应的 dp[i][j],最大的值就是 前 i 种物品（每种物品可以选择无限 件）恰好放入容量为 j 的背包所得到的最大总价值。

3. 对比 0/1背包问题

0/1背包就是限制了每种物品的数量（只有一件）每种物品最多取1件，而完全背包则没有限制每种物品数量，每种物品都可以取 k 件（ k = 1,2,3,4…)。

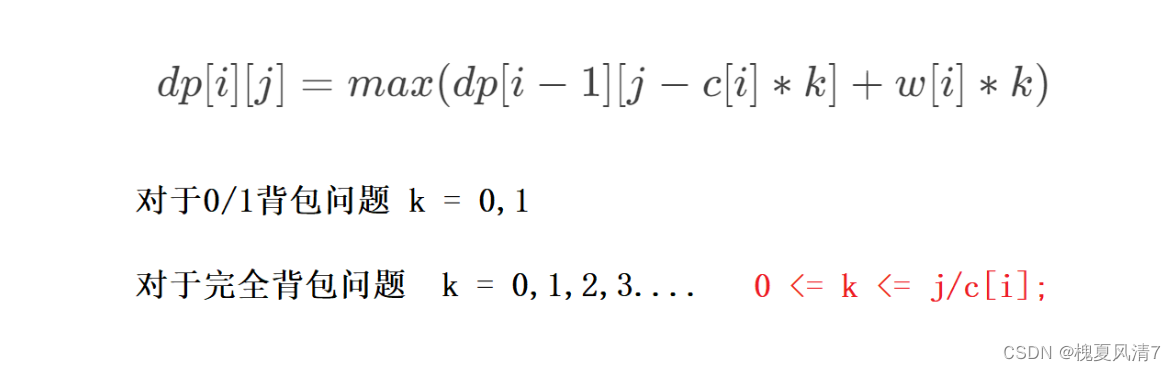
4. 完全背包优化

枚举所有的k,是比较浪费时间的，大量数据可能会超时。

下面优化其时间复杂度

我们发现，这里的 (1)…(k) 式子等价于最开始的状态转移方程中的 (2) … (k+1) 式，所以原状态转移方程可以简化为：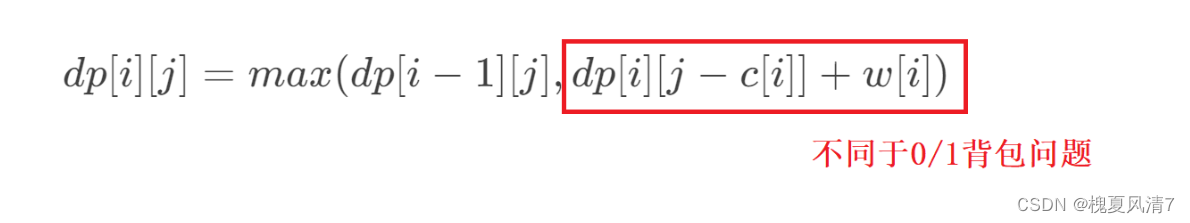

注释： 完全背包的物品是可以添加多次的，所以要从小到大去遍历

先遍历背包还是先遍历物品无所谓。若题目为变形，则需要根据题目确定遍历顺序。

例题：零钱兑换

点击跳转

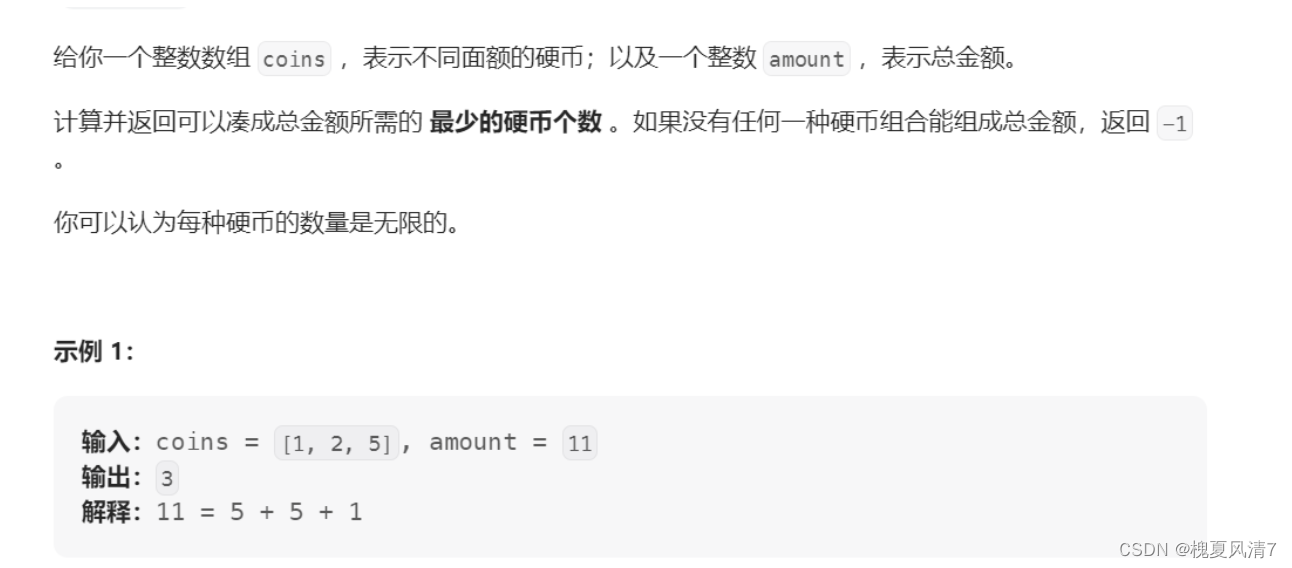
解题思路： 每种硬币的数量是无限的—> 完全背包

设计状态

dp[i][j] 表示[0，i]下标的数，组合为 j 的最少硬币数量

状态转移方程：

dp[i][j]= min( dp[i-1][j],dp[i][j-coins[i]]+1);

初始化状态

// dp[i][j] 来源于 dp[i-1][j-coins[i]] ： 故 dp[0]也需要初始化  
for (int i = 0; i <= coinsSize; ++i) {
        for (int j = 0; j <= amount; ++j) { 
            if (j == 0) dp[i][j] = 0; // 目标金额为0时，需要0个硬币
            else dp[i][j] = INT_MAX / 2; // 其他情况初始化为无穷大
        }
    }
    for (int j = 0; j <= amount; ++j) {
        if(j % coins[0] == 0)  dp[0][j] = j / coins[0];      
    } 

编写代码：

int dp[13][10001];  //表示的是在前i个硬币中凑出金额j所需的最少硬币数量。
int coinChange(int* coins, int coinsSize, int amount) {
   for (int i = 0; i <= coinsSize; ++i) {
        for (int j = 0; j <= amount; ++j) { 
            if (j == 0) dp[i][j] = 0; // 目标金额为0时，需要0个硬币
            else dp[i][j] = INT_MAX / 2; // 其他情况初始化为无穷大
        }
    }
    for (int j = 0; j <= amount; ++j) {
        if(j % coins[0] == 0)  dp[0][j] = j / coins[0];      
    }  
    for (int i = 1; i < coinsSize; ++i) {
        for (int j = 1; j <= amount; ++j) {
            // 不使用当前硬币的情况
            dp[i][j] = dp[i - 1][j];

            // 使用当前硬币的情况
            if (j >= coins[i]) {
                dp[i][j] = fmin(dp[i - 1][j], dp[i][j - coins[i ]] + 1);
            }
        }
    }
    // 检查是否能凑出目标金额
    if (dp[coinsSize-1][amount] == INT_MAX / 2) {
        return -1;
    }

    return dp[coinsSize-1][amount];
}

完全背包类问题的遍历顺序：

1 .外层for循环遍历物品，内层for遍历背包的情况

for (int i = 0; i < coins.size(); i++) { // 遍历物品
    for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
        dp[j] += dp[j - coins[i]];
    }
}

假设：coins[0] = 1，coins[1] = 5。

那么就是先把1加入计算，然后再把5加入计算，得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。

所以这种遍历顺序中dp[j]里计算的是组合数！

如果把两个for交换顺序，代码如下：

for (int j = 0; j <= amount; j++) { // 遍历背包容量
    for (int i = 0; i < coins.size(); i++) { // 遍历物品
        if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
    }
}

背包容量的每一个值，都是经过 1 和 5 的计算，包含了{1, 5} 和 {5, 1}两种情况。

此时dp[j]里算出来的就是排列数！

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。