树和子树的定义

在数据结构中存在一种叫“树”的结构。

树的定义：

树（tree）是由n（n>=0)个节点（或元素）组成的有限集合（记为T）。

如果n=0，它是一棵空树，这是树的特征。如果n大于零，这个n个节点中有且仅有一个节点作为树的根结点，简称为根，其余节点可分为m(m>=0)个互不相干的有限集T1,T2...Tm，其中，每个子集本身又是一颗符合本定义的树，称为根结点的子树

树形的表示方法：

用一个圆圈表示一个节点，圆圈内的符号代表该节点的数据信息，节点之间的关系，通过连线表示，虽然每条连线上都不带有箭头（方向），但他们仍然是有方向的。

如a图所示的表示树形的方法叫做文形图表示法

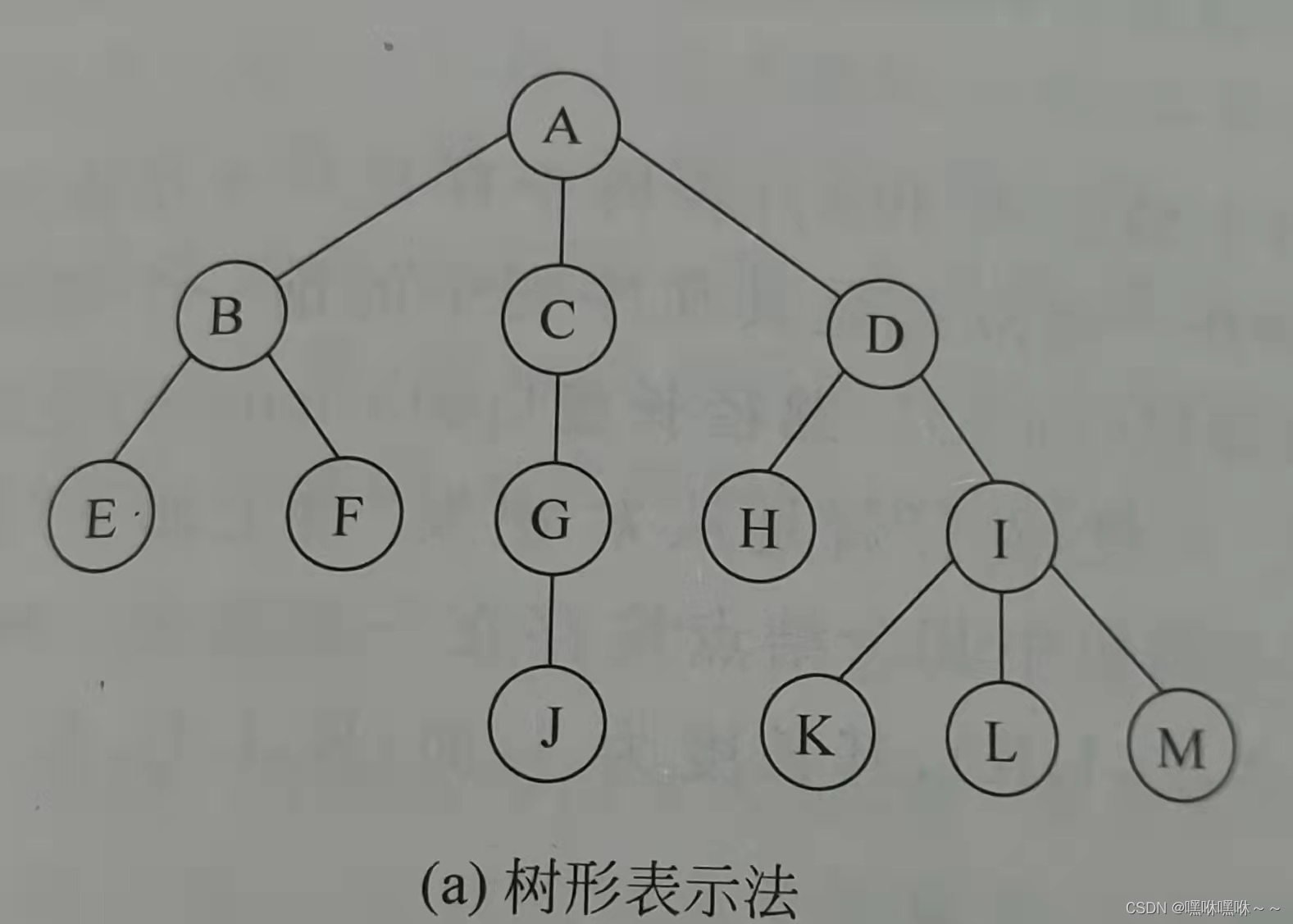
关于树和子树的关系我们可以来举两个例子（学长的PPT截屏）

 了解了以后我们可以来推导一个特殊图形它所包含的子树