搜索二叉树

已于 2024-03-01 17:54:00 修改
阅读量706 收藏 23
点赞数 20
分类专栏： 数据结构学习笔记 文章标签： 算法 数据结构 c++ 后端 开发语言
于 2024-03-01 17:53:23 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_64521581/article/details/136378277
版权

搜索二叉树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
  • 它的左右子树也分别为二叉搜索树

通俗来说，左节点的值要比其根节点的值小， 右节点的值要比其根节点的值大。

例子：

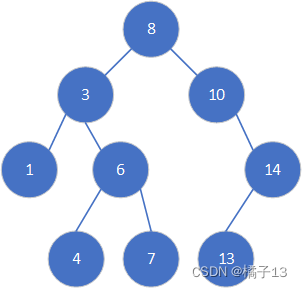
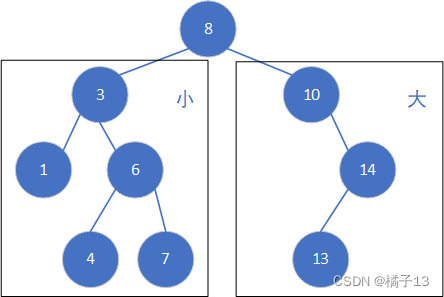
搜索二叉树的功能介绍及实现

基本函数

搜索二叉树节点

template<class K>
struct BSTreeNode
{
	typedef BSTreeNode<K> Node;

	Node* _left;
	Node* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{
	}
};

搜索二叉树的成员变量

Node* _root;

构造函数

	BSTree(Node* root = nullptr)
	{
		_root = root;
	}

析构函数

	~BSTree()
	{
		Destroy(_root);
	}
	void Destroy(Node* root)//后序遍历删除
	{
		if (root == nullptr)
			return;

		Destroy(root->_left);
		Destroy(root->_right);
		delete root;
	}

拷贝构造函数

        这里要用深拷贝，用浅拷贝会造成析构两次的后果。

    	Node* Copy(Node* root)
    	{
    		if (root == nullptr)
    			return nullptr;

    		Node* newRoot = new Node(root->_key);
    		newRoot->_left = Copy(root->_left);
    		newRoot->_right = Copy(root->_right);
    		return newRoot;
    	}

        BSTree(const BSTree<K>& t)//这里要用深拷贝
		{
			_root = Copy(t._root);
		}

		BSTree<K>& operator=(BSTree<K> t)
		{
			swap(_root, t._root);
			return *this;
		}

搜索二叉树的遍历

中序遍历

	void _InOrder(Node* root)//中序遍历
	{
		if (root == nullptr)
		{
			return;
		}
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}

        注意直接调用InOther()需要传根节点，但是我们无法类外访问根节点（根节点访问权限是private）。

解决方法：

1.套一层函数，在类内对根节点进行访问。

	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

使用：

    BSTree<int> t;
	int arr[] = { 8,3,1,10,6,4,7,14,13 };
	for (auto e : arr)
	{
		t.insert(e);
	}
    t._InOrder();

2.写一个获取根节点的函数，实现在类外访问根节点。 

	Node* GetRoot()
	{
		return _root;
	}

使用：

    BSTree<int> t;
	int arr[] = { 8,3,1,10,6,4,7,14,13 };
	for (auto e : arr)
	{
		t.insert(e);
	}
    t._InOrder(t.GetRoot());

缺陷是类外访问了private的成员，不安全。 

搜索二叉树的查找

非递归版本

        直接进行比较，将插入的key值与cur节点的值进行比较，比cur节点大将cur更新为右孩子节点，比cur节点小就将cur更新为左孩子节点，直到遇到key值与cur节点值相同的情况，返回true，若最后遇到空则返回false。

	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
		return false;
	}

递归版本 

	    bool FindR(const K& key)
		{
			return _FindR(_root, key);
		}

        bool _FindR(Node* root, const K& key)
		{
			if (root == nullptr)
				return false;

			if (root->_key < key)
			{
				return _FindR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _FindR(root->_left, key);
			}
			else
			{
				return true;
			}
		}

搜索二叉树的插入

功能：给一个值，插入在二叉搜索树合适的位置（不能插入相同的值）。

非递归版本

        直接进行比较，将插入的key值与cur节点的值进行比较，向左右节点进行移动直到遇到空时插入到该位置，此过程需要保存上一个节点的位置用来进行插入节点。

	bool insert(const K& key)
	{
		//检查空树，防止parent==null时直接访问其成员
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		if (parent->_key < key)
		{
			//连接右节点
			parent->_right = cur;
		}
		else
		{
			//连接左节点
			parent->_left = cur;
		}
	}

递归版本

		bool InsertR(const K& key)
		{
			return _InsertR(_root, key);
		}
        bool _InsertR(Node*& root, const K& key)
		{
			if (root == nullptr)
			{
				root = new Node(key);
				return true;
			}

			if (root->_key < key)
			{
				return _InsertR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _InsertR(root->_left, key);
			}
			else
			{
				return false;
			}
		}

搜索二叉树的删除

        功能：给定一个值（这里是查找的功能，实际上找到了的是这个值所在的节点），删除该节点。

非递归版本

首先是要找到要删除的节点，这一步与之前查找一样，我们把大致的框架搭建起来：

        Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)//待找节点比cur节点值大
			{
				parent = cur;//存一下父节点
				cur = cur->_right;//cur移动到右节点
			}
			else if (cur->_key > key)//待找节点比cur节点值大
			{
				parent = cur;
				cur = cur->_left;
			}
			else//找到了该节点
			{
                //对节点进行删除
            }
        }

下面对删除节点进行分析

情况分析：对于要删除的节点有三种情况

1.该节点无子节点

        直接对该节点进行删除。该步骤可以归到2中，因为可以把nullptr当做一个节点连接到父节点中。

2.该节点仅有一个子节点

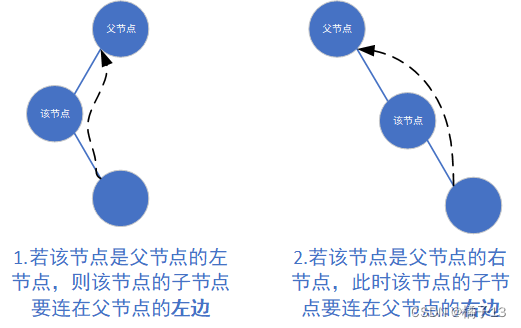
        托孤法删除：将该节点的子节点连接到该节点的父节点，再删除该节点。

       1.当该节点有父节点时

                根据该节点的父节点的位置不同，有两种情况：

                1.该节点是父节点的左节点

                2.该节点是父节点的右节点

                if (cur->_left == nullptr)
				{

						if (cur == parent->_right)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}

					    delete cur;
					    return true;
				}
				else if (cur->_right == nullptr)
				{

						if (cur == parent->_right)
						{
							parent->_right = cur->_left;
						}
						else
						{
							parent->_left = cur->_left;
						}

					    delete cur;
					    return true;
				}

        2.当该节点无父节点时，此时该节点是根

				if (cur->_left == nullptr)
				{
					if (cur == _root)//直接删根时，将根进行转让
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_right)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}
					}

					delete cur;
					return true;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)//直接删根时，将根进行转让
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_right)
						{
							parent->_right = cur->_left;
						}
						else
						{
							parent->_left = cur->_left;
						}
					}

					delete cur;
					return true;
				}

3.该节点有两个子节点

        无法用托孤法将孩子节点连接到父亲节点，因为有两个孩子都连接到父节点，可能会导致父节点出现三个子节点的情况，不符合二叉树的结构。

        替换法删除：找一个能替换“要删除的节点”的节点a，交换值，转换为删除a节点。

        什么节点能替换？

  • 左子树的最大节点（左子树的最右节点）
  • 右子树的最小节点（右子树的最左节点）

        原因：（以左子树的最左节点为例）以要删除的节点为基准，这个节点的值一定小于右子树的所有节点的值，大于左子树的所有节点。这时找到左子树的最左节点，记为Mi点，该节点是左子树的最小的节点，但也大于基准节点的值，这个Mi节点与基准点是相邻的（按大小关系来说），交换两个相邻的节点不改变其他位置的顺序关系，也就是仅增加一个逆序数，这个时候将Mi点删除后，这个逆序数消失，所有数的相对位置关系都变成顺序。

        替换法的代码如下：

					Node* rightMinParent = cur;
					Node* rightMin = cur->_right;
					while (rightMin->_left)//在右子树找到最左节点
					{
						rightMinParent = rightMin;
						rightMin = rightMin->_left;
					}

					cur->_key = rightMin->_key;//将最左节点的值赋给待删节点的值

					if (rightMin == rightMinParent->_left)
					{
						rightMinParent->_left = rightMin->_left;
					}
					else
					{
						rightMinParent->_right = rightMin->_right;
					}
					delete rightMin;
					return true;

        综合这几种情况，总代码如下： 

	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)//待找节点比cur节点值大
			{
				parent = cur;//存一下父节点
				cur = cur->_right;//cur移动到右节点
			}
			else if (cur->_key > key)//待找节点比cur节点值大
			{
				parent = cur;
				cur = cur->_left;
			}
			else//找到了该节点
			{
				//进行删除
				if (cur->_left == nullptr)
				{
					if (cur == _root)//直接删根时
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_right)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}
					}

					delete cur;
					return true;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_right)
						{
							parent->_right = cur->_left;
						}
						else
						{
							parent->_left = cur->_left;
						}
					}

					delete cur;
					return true;
				}
				else//当两个节点都不为空时，替换法
				{
					Node* rightMinParent = cur;
					Node* rightMin = cur->_right;
					while (rightMin->_left)
					{
						rightMinParent = rightMin;
						rightMin = rightMin->_left;
					}

					cur->_key = rightMin->_key;

					if (rightMin == rightMinParent->_left)
					{
						rightMinParent->_left = rightMin->_left;
					}
					else
					{
						rightMinParent->_right = rightMin->_right;
					}
					delete rightMin;
					return true;
				}
			}
		}
		return false;
	}

递归版本

		bool EraseR(const K& key)
		{
			return _EraseR(_root, key);
		}
        bool _EraseR(Node*& root, const K& key)
		{
			if (root == nullptr)
				return false;

			if (root->_key < key)
			{
				return _EraseR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _EraseR(root->_left, key);
			}
			else
			{
				Node* del = root;
				if (root->_right == nullptr)
				{
					root = root->_left;
				}
				else if (root->_left == nullptr)
				{
					root = root->_right;
				}
				else
				{
					Node* rightMin = root->_right;
					while (rightMin->_left)
					{
						rightMin = rightMin->_left;
					}

					swap(root->_key, rightMin->_key);

					return _EraseR(root->_right, key);
				}

				delete del;
				return true;
			}
		}

搜索二叉树的类型

K模型：快速查找一个值在不在

        上文中就是一个K模型，给定key值查找的是key值。

        例子：彩票，直接通过号码在库中查找是否中奖。

KV模型：快速通过一个值（key）查找另一个值（value）在不在？

        在节点的结构体中加入一个value值，这样通过key值查找到节点时，可以访问节点的value值，从而实现了通过一个值（key）查找另一个值（value）。

template<class K,class V>
struct BSTreeNode
{
	typedef BSTreeNode<K,V> Node;

	Node* _left;
	Node* _right;
	K _key;
	V _value;
	BSTreeNode(const K& key,const K& value)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
		,_value(value)
	{
	}
};

        例子：英文字典，通过英文查找释意。

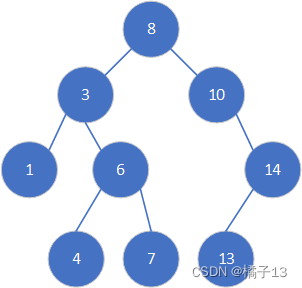
搜索二叉树性能分析

        对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树查找长度是节点在二叉搜索树的高度，即节点越深，则比较次数越多。
        最优情况：二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为：log^N_{2}
       

        最坏情况：二叉搜索树退化为单支树(或者类似单支)，其平均比较次数为：$\frac{N}{2}$

橘子13
关注
  • 20
    点赞
  • 踩
  • 23
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 0
    评论
专栏目录
搜索二叉树c语言版本
08-13
搜索二叉树（Binary Search Tree，简称BST）是一种特殊的二叉树数据结构，它具有以下特性：对于树中的任意一个节点，其左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。...
js实现搜索二叉树.rar
06-08
在JavaScript中实现二叉树是一种常见且重要的编程技巧，它涉及到数据结构和算法的理解。二叉树是一种非线性数据结构，每个节点最多有两个子节点，通常分为左子节点和右子节点。在这个主题中，我们将深入探讨如何使用...
【数据结构】——搜索二叉树的插入，查找和删除（递归&非递归）
02-26
【数据结构】——搜索二叉树的插入，查找和删除（递归&非递归） 在计算机科学中，数据结构是存储和组织数据的方式，它直接影响到数据的处理效率。搜索二叉树（BST，Binary Search Tree）是一种特殊类型的数据结构，...
数据结构搜索二叉树.rar
07-16
二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树...
搜索二叉树的各种操作 创建 查找 遍历 插入 删除
01-20
搜索二叉树的各种操作 创建 查找 遍历 插入 删除 在GCC下编译通过。
函数模板与类模板
程序员_小兵
07-12 1296
/交换int数据a = b;b = temp;//交换char数据a = b;b = temp;//问题：如果我要交换double类型数据，那么还需要些一个double类型数据交换的函数//繁琐，写的函数越多，当交换逻辑发生变化的时候，所有的函数都需要修改，无形当中增加了代码的维护难度//如果能把类型作为参数传递进来就好了，传递int就是Int类型交换，传递char就是char类型交换//我们有一种技术，可以实现类型的参数化---函数模板。
【代码随想录_Day27】509 斐波那契数 70 爬楼梯 746 使用最小花费爬楼梯
qq_43671872的博客
07-08 871
509 斐波那契数70 爬楼梯746 使用最小花费爬楼梯今天的题目难度不低，尽量还是写一些简洁代码 ^ _ ^
2024C++信息素养大赛-算法创意实践挑战_复赛真题（广东省）题目+参考答案和详细解析
m0_74586426的博客
07-12 308
2024C++信息素养大赛-算法创意实践挑战_复赛真题（广东省）题目+参考答案和详细解析
算法刷题笔记 KMP字符串（C++实现，并给出了求next数组的独家简单理解方式）
最新发布
hanmo22357的博客
07-12 483
一道经典且较难的算法题，给出了C++代码实现，以及自己对next数组求解的独家简单的理解方式。
代码随想录算法训练营第33天
m0_62262158的博客
07-10 134
【代码】代码随想录算法训练营第33天。
【代码随想录算法训练营第六十二天|卡码网53.寻宝（prim算法和kruskal算法）】
weixin_46281930的博客
07-09 462
kruskal算法以边为导向，先把边按照长度从小到大排序，然后一个个检查边的两个端点是否在同一个集合中（这里使用并查集判断），在同一个集合中就不加入这个边，不在的话就加入。可以把所有已经使用过的结点看作一个整体，然后把他们相接的结点的结点顶点边中进行选择，选择最短的一条边把该结点入树，某种程度来说也是一种贪心？1.选择当前最短入树结点；3.更新结点距离最小生成树的距离。
C语言力扣刷题12——合并区间[排序]
why1249777255的博客
07-09 431
C语言，合并区间，二维数组的快速排序，qsort，中等难度。
【代码随想录】【算法训练营】【第62天】 [卡码108]冗余连接 [卡码109]冗余连接II
weixin_54954007的博客
07-08 581
思路及算法思维，指路。题目来自。day 62，又是一个周一，ding~
Leetcode104.求二叉树的最大深度
知道这个有什么用？
07-10 279
【代码】Leetcode104.求二叉树的最大深度。
代码随想录算法训练营day76 | Floyd 算法精讲、A * 算法精讲
sunflowers11的博客
07-09 407
本次题目来自于卡码网。
GANs算法简介、学习步骤及具体实现
weixin_41850878的博客
07-08 1231
生成对抗网络（Generative Adversarial Networks，GANs）自从2014年由Ian Goodfellow等人提出以来，已经成为深度学习领域中最活跃的研究方向之一。GAN的基本思想是利用两个神经网络——生成器（Generator）和判别器（Discriminator）——之间的对抗训练，生成器尝试生成逼真的样本以欺骗判别器，而判别器则试图区分生成的样本和真实的样本。随着时间的推移，两个网络相互竞争，最终生成器学会生成高质量的样本。
算法训练营day26--455.分发饼干+376. 摆动序列+53. 最大子序和
qq_42029265的博客
07-08 460
455.分发饼干+376. 摆动序列+53. 最大子序和
Sentinel限流算法：滑动时间窗算法、漏桶算法、令牌桶算法。拦截器定义资源实现原理
qq_44027353的博客
07-12 700
‌例如，‌可以使用一个环形数组来存储时间窗口内的数据点，‌数组的大小等于时间窗口的大小（‌以时间单位为单位）‌。‌每当有新的数据点进入时，‌旧的对应时间点的数据将被覆盖，‌从而实现滑动时间窗的效果。而且，当桶满了之后，多余的水将会溢出。‌随着时间的推移，‌新的数据点进入窗口，‌而旧的数据点则被移出窗口，‌从而形成了一个滑动的时间窗口。我们引入了下面的依赖，也就是我们实际使用sentinel的场景下，我们会发现我们controller层编写的http请求接口都不需要我们自己额外的定义资源开启保护。
Linux C语言基础 day6
没有百宝袋的哆啦A梦的博客
07-08 1352
套路：将数组中的第一个先设置成当前的最值，然后拿着当前的最值与数组中的任意一个元素进行比较，如果比较过程中，不满足条件，则更新最值，直到所有数据都跟最值比较一番后，得出最值。printf("当前数组的最大值为：%d, 在数组的第%d个位置\n", max, maxi+1);2.部分初始化：初始化元素的个数，小于数组的长度，此时，默认从前面元素进行初始化，没有初始化的元素用0补齐。//更新最值中的数据。3.特殊初始化：在定义数组并初始化时，可以不用给定数组的长度，数组的长度由初始化元素个数而定。
C++实现搜索二叉树
05-30
可以使用结构体和指针来实现搜索二叉树，具体实现方法如下： ```c++ #include using namespace std; // 定义二叉树节点结构体 struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x)...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

橘子13

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值