机器学习—PCA算法

一、PCA算法

1. PCA算法介绍

主成分分析（Principal Component Analysis，PCA）是一种用于降维和特征提取的线性变换方法。它通过找到数据中的主成分，将数据映射到一个新的坐标系，以减少数据的维度。

2. PCA算法的原理

PCA的原理在于找到数据中方差最大的方向，即主成分，通过将数据投影到这些主成分上，实现降维。主成分是原始特征的线性组合，每个主成分都是彼此正交的。

3. PCA求解步骤

PCA的求解步骤涉及到特征值分解和线性代数的知识。下面将详细解释PCA的求解步骤，包括相关的公式和矩阵运算。

Step 1: 数据标准化

对原始数据矩阵 X 进行标准化，将每个特征缩放到均值为0，标准差为1。标准化后的数据矩阵记为 ​。

Step 2: 计算协方差矩阵

协方差矩阵 C 是标准化后数据矩阵 的转置与其自身的乘积，除以样本数：

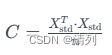
其中，n 是样本数。

Step 3: 计算特征值和特征向量

通过对协方差矩阵 C 进行特征值分解，得到特征值 λ 和相应的特征向量矩阵 V。

特征向量矩阵 V 的列向量即为主成分，而对应的特征值 λ 表示数据在该主成分上的方差。

Step 4: 选择主成分

按特征值的大小降序排列，选择前 k 个特征值对应的特征向量构成矩阵 。

Step 5: 构造新的特征空间

将标准化后的数据矩阵 乘以选定的主成分矩阵 ，得到降维后的数据矩阵 Z。

最终，降维后的数据矩阵 Z 就是通过PCA得到的新特征空间。

总结

整个PCA的求解过程涉及到矩阵的乘法、特征值分解等线性代数运算，通过这些运算，我们能够找到原始数据中最主要的方向，从而实现降维。PCA的本质是将原始特征通过线性变换，转换为新的基下的坐标，以保留最大的方差信息。

4. PCA算法的降维准则

PCA的降维准则主要涉及到对特征值的利用，通过选择一定数量的主成分（特征向量）来实现数据降维。降维准则通常以保留数据总方差的百分比或者设定特征值的阈值为基础。

降维准则的表达：

1. 保留总方差的百分比：

   • 假设我们希望保留的总方差百分比为 γ，则选择前 k 个主成分，使得它们对总方差的贡献达到 γ。即其中，λi​ 是第 i 个特征值，n 是总特征数。
   • 设定特征值的阈值：
     • 设定一个特征值的阈值 ，选择所有特征值大于等于该阈值的主成分。即

具体实现步骤：

1. 计算特征值和特征向量：

   • 对协方差矩阵进行特征值分解，得到特征值 λi​ 和对应的特征向量。

2. 排序特征值：

   • 将特征值按降序排列，选择前 k 个特征值对应的特征向量。

3. 计算方差百分比：

   • 计算所选择的特征值对总方差的贡献百分比。

4. 确定降维维度：

   • 根据降维准则，选择合适的主成分数量 k。

5. 构造新特征空间：

   • 利用选定的主成分构造新的特征空间。

代码示例：

def pca(X, target_variance=0.95):
    # ... (前面的PCA实现步骤)
    
    # 计算方差百分比
    explained_variance_ratio = eigenvalues / np.sum(eigenvalues)
    cumulative_explained_variance_ratio = np.cumsum(explained_variance_ratio)
    
    # 确定要保留的主成分个数
    num_components = np.argmax(cumulative_explained_variance_ratio >= target_variance) + 1
    
    # ... (继续后面的PCA实现步骤)

二、PCA算法的代码实现

import numpy as np

def pca(X, target_variance=0.95):
    # Step 1: 数据标准化
    mean = np.mean(X, axis=0)
    std = np.std(X, axis=0)
    standardized_X = (X - mean) / std
    
    # Step 2: 计算协方差矩阵
    covariance_matrix = np.cov(standardized_X, rowvar=False)
    
    # Step 3: 计算特征值和特征向量
    eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)
    
    # Step 4: 选择主成分
    total_variance = np.sum(eigenvalues)
    explained_variance_ratio = eigenvalues / total_variance
    cumulative_explained_variance_ratio = np.cumsum(explained_variance_ratio)
    
    # 确定要保留的主成分个数
    num_components = np.argmax(cumulative_explained_variance_ratio >= target_variance) + 1
    selected_eigenvectors = eigenvectors[:, :num_components]
    
    # Step 5: 构造新的特征空间
    new_X = np.dot(standardized_X, selected_eigenvectors)
    
    # 可选：重构原始数据
    reconstructed_X = np.dot(new_X, selected_eigenvectors.T)
    
    return new_X, reconstructed_X, num_components

# 示例用法
# 假设X是一个m x n的数据矩阵，m是样本数，n是特征数
# new_X是降维后的数据，reconstructed_X是重构的数据，num_components是保留的主成分个数
new_X, reconstructed_X, num_components = pca(X)

print(f"降维后的数据:\n{new_X}")
print(f"重构的数据:\n{reconstructed_X}")
print(f"保留的主成分个数: {num_components}")

这个代码示例中，通过设定目标方差百分比，选择合适的主成分个数，同时还提供了对降维后的数据进行重构的功能。此外，还计算了每个主成分对总方差的贡献百分比，以便更灵活地选择降维的维度。三、PCA算法优缺点

三.PCA算法优缺点

优点：

• 降维效果显著，减少了特征数量。
• 去除了特征间的冗余信息，保留了主要特征。

缺点：

• 只能处理线性关系，对于非线性关系的数据降维效果有限。
• 在某些情况下，信息损失较大，需要谨慎选择主成分的数量。