In mathematics, a principal branch is a function which selects one branch (“slice”) of a multi-valued function. Most often, this applies to functions defined on the complex plane.
Contents
1 Examples
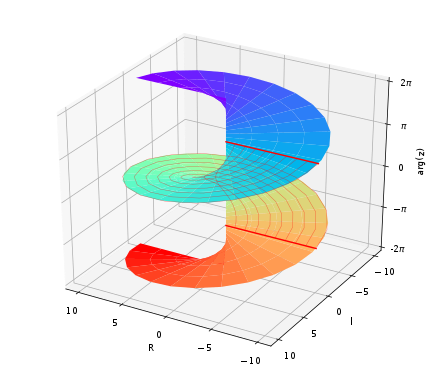
Principal branch of arg(z)
1.1 Trigonometric inverses
Principal branches are used in the definition of many inverse trigonometric functions, such as the selection either to define that
{\displaystyle \arcsin :[-1,+1]\rightarrow \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}{\displaystyle \arcsin :[-1,+1]\rightarrow \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}
or that
{\displaystyle \arccos :[-1,+1]\rightarrow [0,\pi ]}{\displaystyle \arccos :[-1,+1]\rightarrow [0,\pi ]}.
1.2 Exponentiation to fractional powers
A more familiar principal branch function, limited to real numbers, is that of a positive real number raised to the power of 1/2.
For example, take the relation y = x1/2, where x is any positive real number.
This relation can be satisfied by any value of y equal to a square root of x (either positive or negative). By convention, √x is used to denote the positive square root of x.
In this instance, the positive square root function is taken as the principal branch of the multi-valued relation x1/2.
1.3 Complex logarithms
One way to view a principal branch is to look specifically at the exponential function, and the logarithm, as it is defined in complex analysis.
The exponential function is single-valued, where ez is defined as:
{\displaystyle e{z}=e{a}\cos b+ie^{a}\sin b}e{z}=e{a}\cos b+ie^{a}\sin b
where {\displaystyle z=a+ib}z=a+ib.
However, the periodic nature of the trigonometric functions involved makes it clear that the logarithm is not so uniquely determined. One way to see this is to look at the following:
{\displaystyle \operatorname {Re} (\log z)=\log {\sqrt {a{2}+b{2}}}}\operatorname {Re} (\log z)=\log {\sqrt {a{2}+b{2}}}
and
{\displaystyle \operatorname {Im} (\log z)=\operatorname {atan2} (b,a)+2\pi k}\operatorname {Im} (\log z)=\operatorname {atan2} (b,a)+2\pi k
where k is any integer and atan2 continues the values of the arctan(b/a)-function from their principal value range {\displaystyle (-\pi /2,;\pi /2]}{\displaystyle (-\pi /2,;\pi /2]}, corresponding to {\displaystyle a>0}a>0 into the principal value range of the arg(z)-function {\displaystyle (-\pi ,;\pi ]}{\displaystyle (-\pi ,;\pi ]}, covering all four quadrants in the complex plane.
Any number log z defined by such criteria has the property that elog z = z.
In this manner log function is a multi-valued function (often referred to as a “multifunction” in the context of complex analysis). A branch cut, usually along the negative real axis, can limit the imaginary part so it lies between −π and π. These are the chosen principal values.
This is the principal branch of the log function. Often it is defined using a capital letter, Log z.
2 See also
Branch point
Branch cut
Complex logarithm
Riemann surface























 1792
1792











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








