练习题 —— 约瑟夫环问题

我们今天来看一个比较头痛的问题——约瑟夫环

约瑟夫环的背景

约瑟夫环的背景是来自一个故事：

据说著名犹太历史学家Josephus（弗拉维奥·约瑟夫斯）有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。问题是，给定了和，一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

约瑟夫环有各种变形的题目：猴子选大王，破冰游戏等等：

https://leetcode.cn/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/

这道题的的难点就是每次重新开始报数的位置不固定，因为有循环的取模的操作，导致每次重新报数的位置变化可能很大。

一般操作

如果是刚开始接触这个问题，可以用链表或者数组模拟，这里给出伪代码：

#include <iostream> // 确保包含输入输出流头文件

using namespace std;

int main()
{
    bool a[101] = {0}; // 初始化一个大小为101的布尔数组，用于标记位置是否有人，默认为无人

    int n, m, i, f = 0, t = 0, s = 0; // 初始化变量
    cin >> n >> m; // 输入总人数n和报数到m时杀人
    // 开始循环，直到所有人都被杀死
    do
    {
        // 逐个枚举圈中的位置，模拟报数过程
        ++t; // 递增位置计数器
        if (t > n) // 如果超过总人数，则回到起始位置（环状结构）
            t = 1;

        // 如果当前位置无人（a[t]为false），则报数并递增报数计数器
        if (!a[t])
        {
            s++; // 报数

            // 如果报数到m，则执行杀人操作
            if (s == m)
            {
                s = 0; // 报数计数器重置为0，开始新一轮报数
                cout << t<< "号位置" << endl; // 输出被杀的人的编号
                a[t] = 1; // 标记当前位置已无人
                f++; // 死亡人数加1
            }
        }
        // 注意：如果当前位置已有人（a[t]为true），则不执行报数和杀人操作，直接继续下一个位置
    } while (f != n); // 循环直到所有人都被杀死

    return 0; // 程序正常结束
}

这样有个问题，如果人很多，我就要开一个很大的数组，很消耗空间，并且容易超时，那该怎么办呢？

其实约瑟夫环有专门的公式，我们下面就来推导一下：

公式推导

我们知道一开始，从0开始报数：

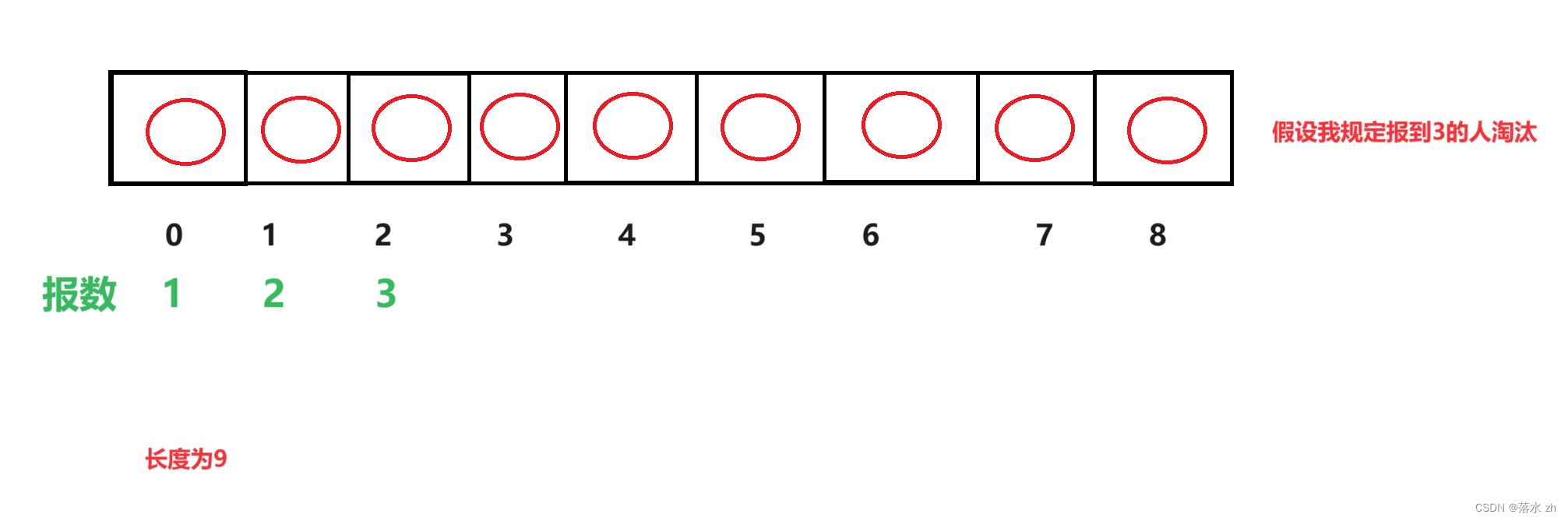
然后2号位置被淘汰：
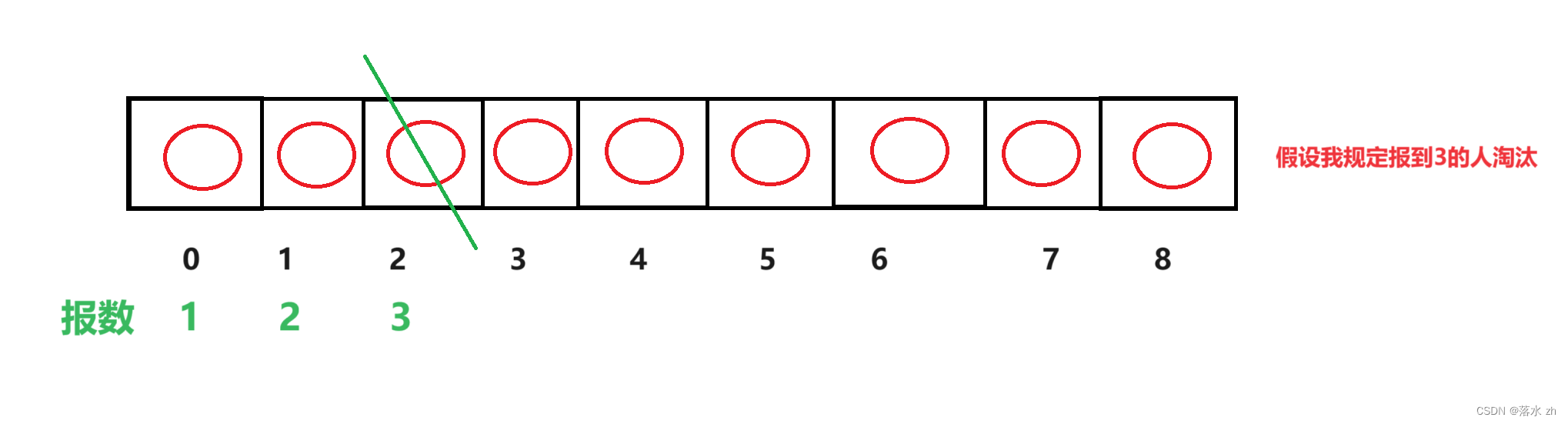然后我们往后走：

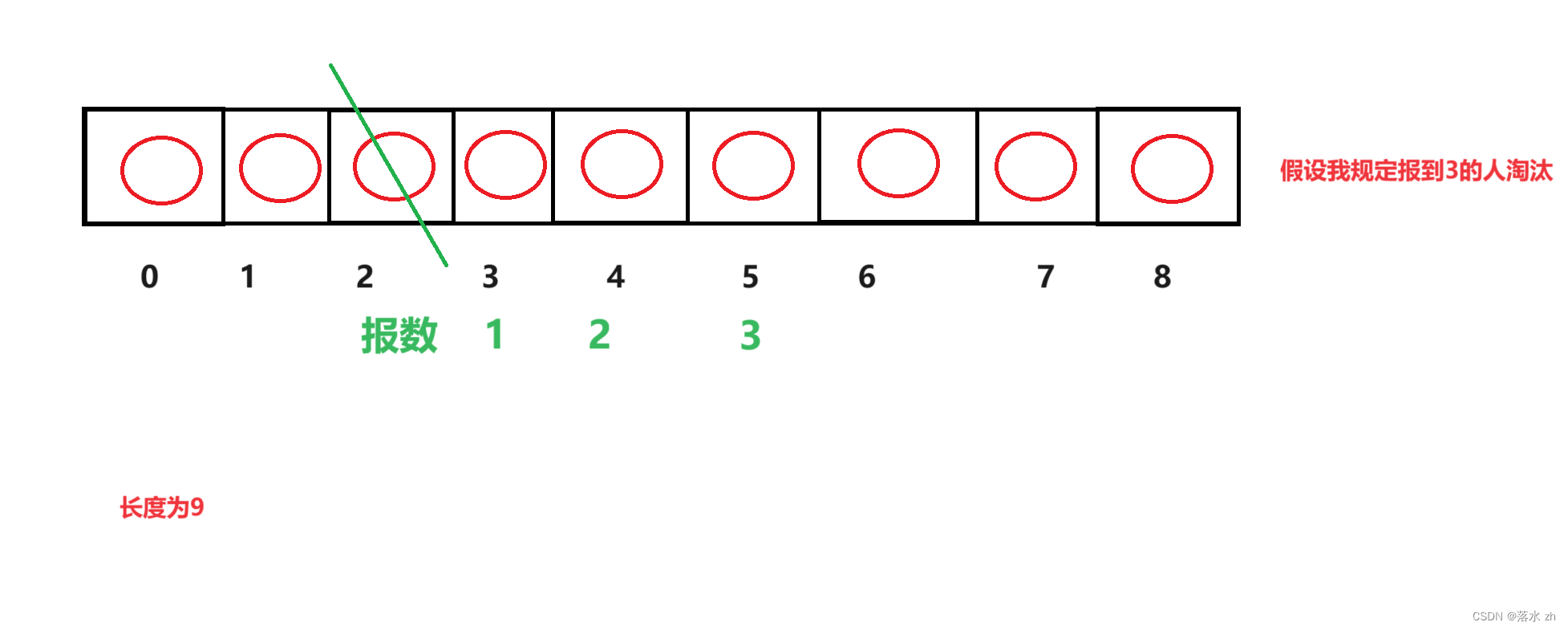
这个时候，我们做一个变换，为了方便我们观察，我们把0,1号位置的人放在后面：

我们这个时候重新给各个位置的人编号：

这样，通过重新编号之后，我们可以得到一个事实最后活下来的是0号位置（这点很重要）
这个时候我们的0号位是最终的结果，现在我们可以根据这个结果反推当两个人的时候，胜利者在上一轮的编号为多少

我们是数到3淘汰，只有2个人，有循环的操作，所以我们要加取模操作：

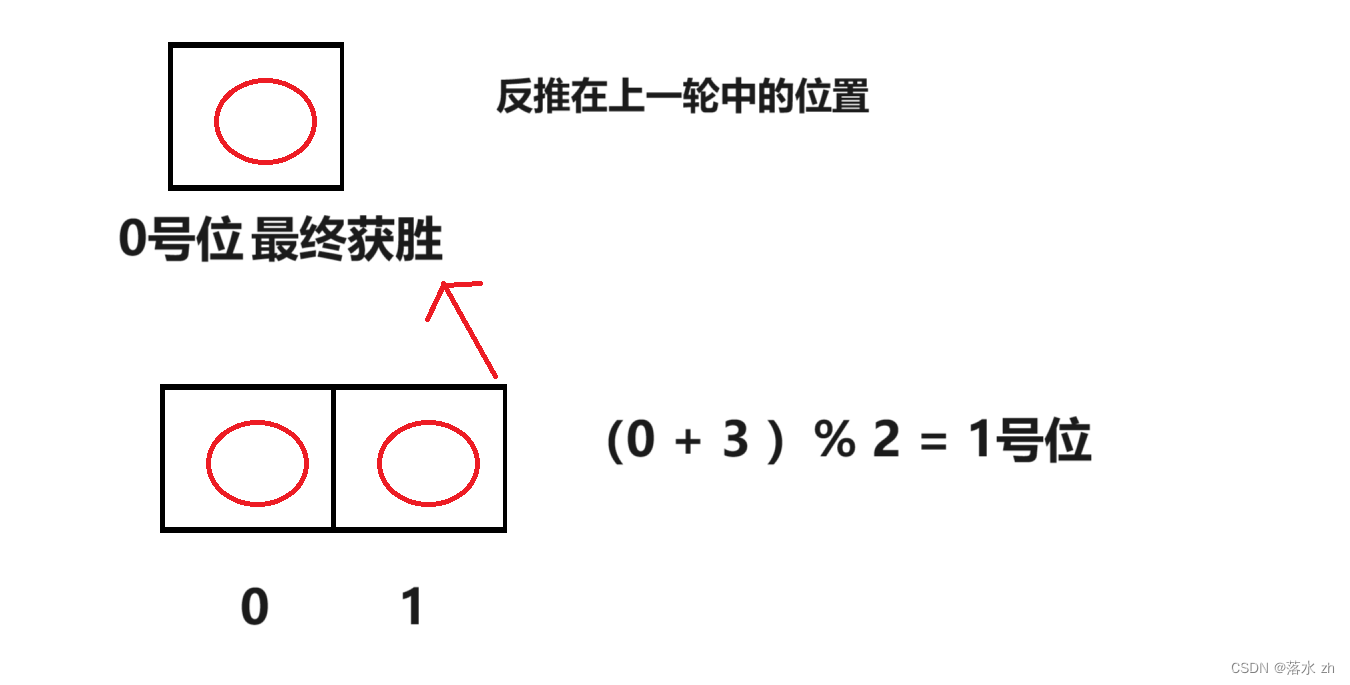
我们知道了倒数第二轮的，就可以推出倒数第三轮的：

这样我们可以得出一个递推公式：

当前存活位置 = （上一轮存活位置 + 夺命数）% 上一轮人数

什么时候停止呢？恢复到一开始的人数就行了：

#include <iostream> 
using namespace std;

void function(int number_people,int kill_number)
{
    int survivor = 0; // 最后存活位置
    for(int i = 2; i <=number_people; i++) //从倒数第二轮开始复盘
    {
        survivor = (survivor + kill_number) % i;
        cout << survivor << "号位置存活" << endl; // 输出被杀的人的编号
    }
}

int main()
{
    function(10,3);
}

递归版本

可以用迭代，一般也可以用递归：

#include <iostream> 
using namespace std;

int function2(int number_people,int kill_number)
{
    if(number_people == 1)
    {
        return 0;
    }

    int survivor = function2(number_people - 1,kill_number);
    
    return (survivor + kill_number) % number_people;
}

int main()
{
    cout << function2(3,3) << "号位置存活" << endl;
}