插值法介绍
通过曲线上若干点,确定一条"简单的"与未知曲线"最接近"的曲线。简单的指多项式函数,最接近指最佳逼近。就是从指定的一类简单的函数中寻找一个和给定的函数“最贴近”的函数,从几何(空间)的角度看,函数最佳逼近就是从指定的一类简单的函数(点的集合)中寻找一个和给定的函数(定点)之间距离最短的函数(点)。函数空间中不同的距离度量确定了不同的逼近准则,不同的逼近准则定义了不同的函数最佳逼近。
一.引言
插值问题:
函数y=f(x),在区间[a,b],已知[a,b]上有n+1个点以及对应的
,其中(i=0~n)。求插值函数P(x)使得P(
)=
。
二.拉格朗日插值
(1)线性插值(n=1)
点斜式直线方程:

两点对称式直线方程

(2)抛物插值(n=2)
拉格朗日插值为
![]()
插值型基函数

展开

插值余项为

![]()
二.牛顿插值

解题步骤:
1构造差商表

根据n的不同取值,写出插值多项式:
(1)线性插值:n=1,
(2)抛物插值:n=2.
插值余项。
三.埃尔米特插值
在某些实际问题中,希望近似多项式能更好的密合原函数,即不但要求插值函数在节点上等于已知函数值,而且还要求其导数值相等.例如,飞机外形曲线,它由几条不同的曲线衔接,此时要求衔接处足够光滑.这种使插值函数和被插值函数密合程度更好的插值问题,称为埃尔米特插值。

三次埃尔米特插值多项式
考虑是n=1的情况,此时插值多项式为
![]()
插值基函数

误差估计:

四.三次样条插值
要求插值多项式S(x)
(1)插值条件:S(x)=y
(2)分段条件:分为了几个区间段
(3)光滑条件:S(x)在[a,b]连续二阶可导
(4)边界条件:第一种边界一阶可导,第二种边界二阶可导,第三种边界n阶可导。
解题思路:
根据区间段数确定方程组次数:n=2
设方程组

由插值条件,连续条件:
(-1) =1,
(0) = 0,
(0) = 0,
(1) =1。

由内节点连续条件
![]()
由边界条件:

解出各系数的值代入方程中:
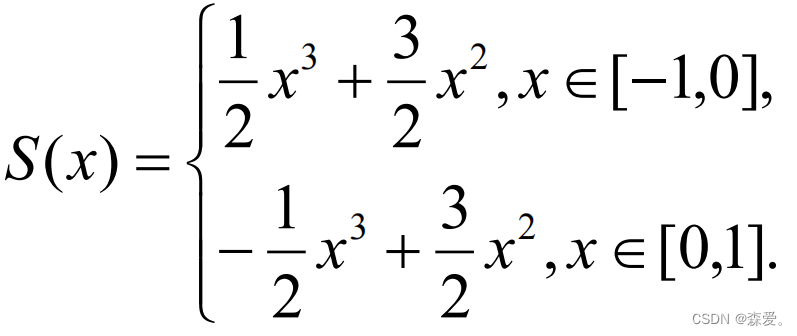

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








