动态规划之背包问题系列(一）

问题描述：

给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

分类：

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。 第 i件物品的体积是 v_i，价值是 w_i。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

问题变形
完全背包：每种物品都有无限多个可用；
多重背包：每种物品有s[i] 个可用；
分组背包：物品有 N组，每一组里面只能选一个物品。
01背包问题 完全背包问题 多重背包问题 ，恰好装满、求方案总数、求所有的方案等

知识点important

dp(动态规划）&&dfs(深度优先）

01背包问题：

一共有N件物品，第i（i从1开始）件物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够装入背包的最大价值是多少？

思路：
如果穷举的话，时间复杂度太大，故dp
定义状态dp:
dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W
初始化，当 i > 0 时dp[i][j]有两种情况：
不装入第i件物品，即dp[i−1][j]；
装入第i件物品（前提是能装下），即dp[i−1][j−w[i]] + v[i]。

即其状态转移方程为：
dp[i][j] = max(dp[i−1][j], dp[i−1][j−w[i]]+v[i]) // j >=w[i]

特别的：为了防止上一层被覆盖，循环采用逆向枚举

// 01背包问题伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
    for j = W,...,w[i] // 必须逆向枚举!!!
        dp[j] = max(dp[j], dp[j−w[i]]+v[i])

采用这个方法的好处是避免了不必要的重复计算

//dfs
#include <stdlib.h>
#include <string.h>



int Knapsack(int* v, int* w, int n, int target) {
//Knapsack 函数接受三个参数：v、w 和 target，分别表示物品的体积、价值和背包的体积。
const int N = n + 1;
//申请大小为 (n+1) x (target+1) 的二维数组 cache 用于存储中间结果
int** cache = (int**)malloc(sizeof(int*) * N);
for (int i = 0; i < N; i++) {
cache[i] = (int*)malloc(sizeof(int) * (target + 1));
memset(cache[i], -1, sizeof(int) * (target + 1));
}
int dfs(int i, int j) {
//定义内部函数 dfs，用于递归求解问题
//参数 i 和 j，分别表示剩余的物品数量和背包的剩余体积
if (i == 0) return 0;//当没有物品可选时，价值为 0
if (cache[i][j] != -1) return cache[i][j];//cache[i][j] 已经有值，直接返回
//cache[i][j] 表示前 i 个物品放入体积为 j 的背包的最大价值
int res = dfs(i - 1, j);
if (j >= v[i - 1]) res = max(res, dfs(i - 1, j - v[i - 1]) + w[i - 1]);
//先递归求解不选第 i 个物品的情况，然后考虑选第 i 个物品
//第 i 个物品的体积超过当前背包剩余的体积，则必须放弃该物品
//放入背包并更新最大价值
cache[i][j] = res;
return res;
}
//调用 dfs(n, target) 求解问题，并释放动态分配的内存
int result = dfs(n, target);
for (int i = 0; i < N; i++) free(cache[i]);
free(cache);
return result;
}

//dfs->dp
#include <string.h>

const int N = 1010;

int Knapsack(int* v, int* w, int n, int target) {
int dp[N][N]; memset(dp, 0, sizeof(dp));//dp 数组全部初始化为 0
//使用两个嵌套的循环来填充 dp 数组中的值
for (int i = 1; i <= n; i ++) {//枚举所有物品
for (int j = 0; j <= target; j ++) {//枚举所有体积
dp[i][j] = dp[i - 1][j];
//不选该物品，背包的价值就是前 i-1 个物品放入 j 体积的背包的价值
//选该物品，背包的价值就是前 i-1 个物品放入 j-v(i) 体积的背包的价值加上第 i 个物品的价值
//将价值较大的作为 dp(i, j) 的值
if (v[i - 1] <= j) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i - 1]] + w[i - 1]);
}
}
return dp[n][target];
}

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])
1、对于每次循环的下一组i，只会用到i-1来更新当前值。于是可以在这次更新的时候，
将原来的值更新掉，反正以后也用不到，所以对于i的更新，只需用一个数组。也就
是滚动数组，每次根据上一层的值更新当前层的值。（优化掉一维）
2、对于每次j的更新，只需用到之前i-1时的j或者j-v[i]，不会用到后面的值，同时为
了防止当前用于更新的之前i-1层的d[j] 或 d[j - v[i]]之前被更新过，采用从后
往前的方式遍历j。（优化j的循环次数）

//dp
//滚动数组的思想来实现空间优化
int Knapsack(int* v, int* w, int n, int target) {
const int N = 1010;
int dp[N]; memset(dp, 0, sizeof(dp));
for (int i = 1; i <= n; i ++) {
for (int j = target; j >= v[i - 1]; j -- ) {
dp[j] = max(dp[j], dp[j - v[i - 1]] + w[i - 1]);
}
}
return dp[target];
}

2. 完全背包

题目
完全背包与01背包不同就是每种物品可以有无限多个：一共有N种物品，每种物品有无限多个，第i（i从1开始）种物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够装入背包的最大价值是多少？

// 完全背包问题**Way1**伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
    for j = w[i],...,W // 必须正向枚举!!!
        dp[j] = max(dp[j], dp[j−w[i]]+v[i])

way2
取0件、1件、2件…直到超过限重（k > j/w[i]）
思路与01问题相同，就是MAX改了

k为装入第i种物品的件数,
k <= j/w[i] dp[i][j] = max{(dp[i-1][j − kw[i]] +kv[i]) for every k}

// 完全背包问题**Way2**伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
    for j = W,...,w[i] // 必须逆向枚举!!!
        for k = [0, 1,..., j/w[i]]
            dp[j] = max(dp[j], dp[j−k*w[i]]+k*v[i])

二进制的思想

把第 i 种物品拆成
重量为

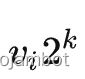
价值为

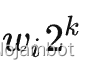
的若干件物品，其中 k 取遍满足
的非负整数。

这是因为不管最优策略选几件第 i 种物品，总可以表示成若干个刚才这些物品的和
这样就将转换后的物品数目降成了对数级别。

#include <stdio.h>
#include <string.h>

#define N 1010

int Knapsack(int *v, int *w, int target, int n) { // target表示背包体积
int dp[N][N];
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= n; i ++ ) {
for (int j = 0; j <= target; j ++ ) {
for (int k = 0; k * v[i - 1] <= j; k ++ ) {
dp[i][j] = (dp[i][j] > dp[i - 1][j - k * v[i - 1]] + k * w[i - 1]) ? dp[i][j] : dp[i - 1][j - k * v[i - 1]] + k * w[i - 1];
}
}
}
return dp[n][target];
}

int main() {
int v[] = {2, 3, 4};
int w[] = {3, 4, 5};
int target = 5;
int n = sizeof(v) / sizeof(int);
printf("The maximum value of the knapsack is %d.\n", Knapsack(v, w, target, n));
return 0;
}

//优化
#include <stdio.h>
#include <string.h>

#define N 1010

int Knapsack(int *v, int *w, int target, int n) { // target表示背包体积
int dp[N][N];
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= n; i ++ ) {
for (int j = 0; j <= target; j ++ ) {
dp[i][j] = dp[i - 1][j];
if (j >= v[i - 1]) dp[i][j] = (dp[i - 1][j] > dp[i][j - v[i - 1]] + w[i - 1]) ? dp[i - 1][j] : dp[i][j - v[i - 1]] + w[i - 1];
}
}
return dp[n][target];
}

int main() {
int v[] = {2, 3, 4};
int w[] = {3, 4, 5};
int target = 5;
int n = sizeof(v) / sizeof(int);
printf("The maximum value of the knapsack is %d.\n", Knapsack(v, w, target, n));
return 0;
}