乘法逆元求解

目录:

乘法逆元小结

一、逆元定义

        1.扩展欧几里得(exgcd)   适用于单个查找或者模p很大的情况下 , p 不是质数的时候也可以使用

        2.快速幂 O(logn)

        3.线性求逆元 (用于求一连串数字对于一个模p下的逆元) O(n)

        4.阶乘逆元 O(n)   只适用于模数为质数的情况

---

乘法逆元小结

乘法逆元，一般用于求

 的值（p 通常为质数），是解决模意义下分数数值的必要手段。

一、逆元定义

 二、求逆元的方法

1.扩展欧几里得(exgcd)   适用于单个查找或者模p很大的情况下 , p 不是质数的时候也可以使用

此处是线性同余方程(a*x≡b(modm))的特殊情况  (b=1)

所求解x1=x*b/d%m,为了保证x1是最小的正整数 因此x1=(x1%m+m)%m

#include<iostream>
using namespace std;
//扩展欧几里得算法
// 对任意一组 ax+by=m 存在一组x，y满足ax+by=gcd(a,b) 即m=gcd(a,b)
int exgcd(int a, int b, int& x, int& y) {
	if (!b) {
		x = 1, y = 0;
		return a;
	}
	int t = exgcd(b, a % b, y, x);
	y = y - a / b * x;
	return t;
}	
int main() {
	int x, y;
	int a, m;
	cin >> a >> m;

	int d = exgcd(a, m, x, y);

	int x1 = x / d % m;
	x1 = (x1 % m + m) % m;
	printf("%d", x1);

	return 0;
}

2.快速幂 O(logk)

首先科普一下费马小定理qaq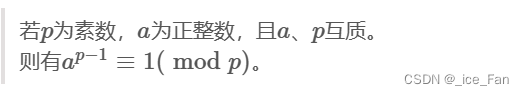

 将这个公式进行变形可以得到下面的式子

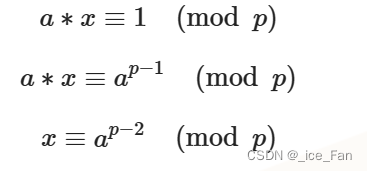
所以我们可以用快速幂来算出的值，这个数就是它的逆元

 Code:    (x为a在mod p意义下的逆元。)

#include<iostream>
using namespace std;
typedef long long ll;
ll qmi(ll a, ll b,ll p) {
	ll res = 1;

	while (b) {
		if (b & 1) res = res * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return res;
}
int main() {
	int a, b, p;
	cin >> a >> b>>p;
	ll x = qmi(a, b - 2,p); 

	return 0;
}

3.线性求逆元 (用于求一连串数字对于一个模p下的逆元) O(n)

Code:

#include<iostream>
using namespace std;
typedef long long LL;
const int N = 3e6 + 10;
int inv[N];
int n, p;
int main() {
	scanf("%d%d", &n, &p);

	inv[1] = 1;

	for (int i = 2; i <= n; i++)
		inv[i] = (LL)(p - p / i) * inv[p % i] % p;


	return 0;
}

4.阶乘逆元 O(n)   只适用于模数为质数的情况

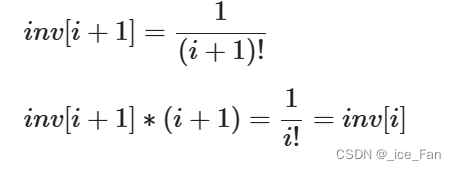
因此我们可以先求出n!然后进行递推来求出1->n!所有的逆元

递推式 :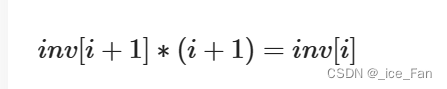  

 最后可以得到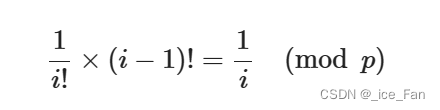

Code:                         a[N]存1->n! b[N]存1->n!的逆元 

#include<iostream>
using namespace std;
typedef long long ll;
const int N = 3e6 + 10;
ll a[N], b[N];
ll n, p;
ll qmi(ll a, ll b, ll p) {
	ll res = 1;
	while (b){
		if (b & 1) res = res * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return res;
}
int main() {
	cin >>n >> p;

	a[0] = 1;
	for (int i = 1; i <= n; i++)
		a[i] = (a[i - 1] * i) % p;

		b[n] = qmi(a[n], p - 2, p);


	for (int i = n - 1; i >= 1; i--) 
		b[i] = (b[i + 1] * (i + 1)) % p;

	for (int i = 1; i <= n; i++)
		cout << b[i] * a[i - 1]%p<<endl;



	return 0;
}

舞台再大，你不上台，永远是个观众。平台再好，你不参与，永远是局外人。能力再大，你不行动，只能看别人成功。没有人会关心你付出过多少努力，撑得累不累，摔得痛不痛，他们只会看你最后站在什么位置，然后羡慕或鄙夷。