The 2023 ICPC Asia EC Regionals Online Contest (I)G题J题K题

题目链接

G. Spanning Tree

容易知道对于一颗树来说，若将其分成若干块，每两块的链接一定是其中一个块的根节点（深度最小的那个点）连向另一个块中的一个点，反之，若不是这样那么生成的树一定不是同一根树。

所以我们只需要记录给定生成树的点的每个点的父节点，最后再用并查集即可，让深度小的当父亲节点。不用lca，用倍增lca的话会超时。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
const int mod=998244353;
//#define int long long
int fa[N][20],dep[N],faa[N],siz[N];
vector<int> v[N];
int n;
pair<int,int> p[N];
long long qpow(int a,int b){
	long long res=1;
	while(b){
		if(b&1) res=((long long)res*a)%mod;
		b>>=1;
		a=((long long)a*a)%mod;
	}
	return res;
}
void dfs(int x,int f){
	dep[x]=dep[f]+1;
	fa[x][0]=f;
/*	for(int i=1;i<=19;i++){
		fa[x][i]=fa[fa[x][i-1]][i-1];
	}*/
	for(int i=0;i<v[x].size();i++){
		int j=v[x][i];
		if(j==f) continue;
		dfs(j,x);
	}
}
int lca(int a,int b){
	if(dep[a]<dep[b])
		swap(a,b);
	for(int i=19;i>=0;i--){
		if(dep[fa[a][i]]>=dep[b])
			a=fa[a][i];
	}
	if(a==b) return a;
	for(int i=19;i>=0;i--){
		if(fa[a][i]!=fa[b][i]){
			a=fa[a][0],b=fa[b][0];
		}
	}
	return fa[a][0];
}
int find(int x){
	if(faa[x]==x)
		return x;
	return faa[x]=find(faa[x]);
}
void u(int a,int b){
	a=find(a),b=find(b);
	if(a!=b){
		if(dep[b]<dep[a])
		siz[b]+=siz[a],
		faa[a]=b;
		else
		siz[a]+=siz[b],
		faa[b]=a;
	}
}
void solve(){
	cin>>n;
	for(int i=1;i<=n;i++)
		faa[i]=i,siz[i]=1;
	for(int i=1;i<n;i++){
		int a,b;cin>>a>>b;
		p[i]={a,b};
	}
	for(int i=1;i<n;i++){
		int a,b;cin>>a>>b;
		v[a].push_back(b);
		v[b].push_back(a);
	}
	dfs(1,0);
	long long ans=1;
	for(int i=1;i<n;i++){
		int a=p[i].first,b=p[i].second;
		a=find(a),b=find(b);
		if(find(b)==find(fa[a][0])||find(fa[b][0])==find(a)){
			ans=((long long)ans*qpow((long long)siz[find(a)]*siz[find(b)]%mod,mod-2))%mod;
			u(a,b);
		}
		else ans=0;
	}
	cout<<ans;
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0);cout.tie(0);
	int t=1;
	//cin>>t;
	while(t--){
		solve();
	}
	return 0;
}

J. Minimum Manhattan Distance

我们将c2的圆心设在原点。由于题目条件x1不等于x2并且y1不等于y2，

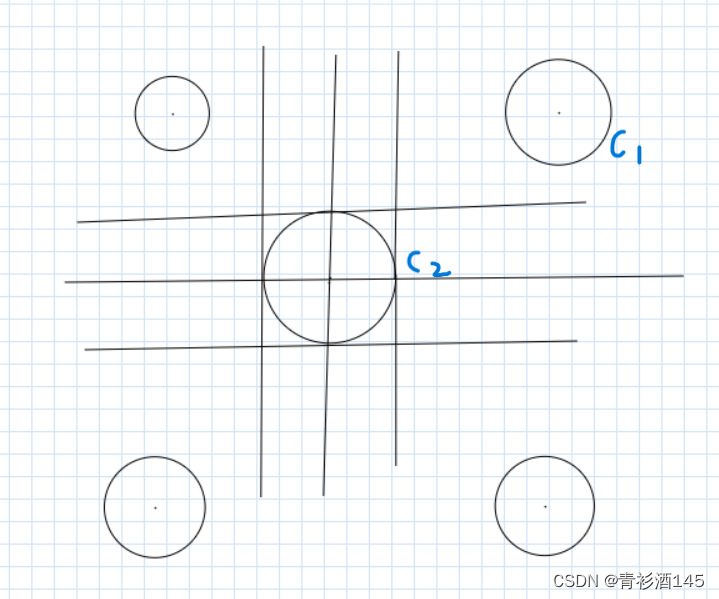
        所以c1所在的位置一定是在c2上下左右顶点与坐标轴平行直线的外面，并且可以通过关于

坐标轴对称到第一象限，即c2的右上角，此时x1>x2 && y1>y2。我们设c1的圆心是（c，d），

c2内任意一点是（a，b）。容易知道对于c2中的一个点到c1内点的期望就是到c1圆心的期望。

证明：

设c1内任意一个点是（x，y），c1的半径为R。

期望等于，，

分子部分即是，。

对于区域不在原点的二重积分我们考虑使用极坐标平移法，

令，

那么（此处的r为极坐标（r，）的r）。

此时极点和c1圆心重合，变成，

合并一下，

再进行拆分和提取常数项

，

即

前者积分值为0，后者积分值为，

所以分子积分值为，

最后再除以分母得c+d-a-b，可知期望值等于c2内一点到c1圆心的曼哈顿距离，证毕。

        当我们知道是到c1圆心期望最小值时，我们就可以进行下一步：找出c2中哪个点

到c1圆心期望最小。

        我们设c2半径为R，c2内一点为（），（a<=R）。那么曼哈顿距离就是

c+d-（），c+d为定值，若要曼哈顿距离最小，就是要（）

最大。再由辅助角公式可知=，又，所以

的最大值为，又a的最大值为R，所以c+d-的最小值

为c+d-。最后的最后，因为c2的圆心不一定在原点，我们将c+d改成两圆的圆心曼哈顿

距离即可，设c2的圆心是（a，b）所以最终结果是c+d-a-b-。

K. Minimum Euclidean Distance

        容易知道一个点到圆内点的欧几里得距离平方为，r是圆的半径，d是点到圆心的距离。

证明：

设点为（a，b），圆心为（c，d），圆内任意一点为（x，y），圆的半径是R，期望就是。

设，

分子即是

将平方拆开合并同类项可得

再拆成多个二重积分之和

且他们的二重积分上下值都是，然后算出三个积分值为，0，，最后分子除以分母得，

即，证毕。

        分类讨论，若圆心在凸包内部则令d为0；若圆心在凸包外部，则遍历凸包的边求

圆心到这些边距离的最小值即可。对于如何判断是否在凸包内部，则逆时针遍历边，用叉积判断凸包的每条边圆心是否在这些边的左边即可。

        叉积中若a*b值为正表示a在b的顺时针方向。求投影可以用a.b=|a|*|b|*cos，由投影判断

点与线段位置关系。求垂线距离可以用叉积求出平行四边形面积再除以底边长。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=3e6+10;
const int inf=0x3f3f3f3f;
typedef long long ll;
typedef pair<int,int> pii;
typedef unsigned long long ull;
//const ll P=2281701377;
const ll P=998244353;

struct point{
    double x,y;
};
struct vec{
    double x,y;
};
double cross(vec a,vec b){
    return a.x*b.y-a.y*b.x;
}
double get_dis(point a,point b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double get_point_mul(vec a,vec b){
    return a.x*b.x+a.y*b.y;
}
vec get_vector(point a,point b){
    vec res={b.x-a.x,b.y-a.y};
    return res;
}
double get_area(point a,point b,point c){
    vec vecb=get_vector(a,b),vecc=get_vector(a,c);
    return fabs(cross(vecb,vecc));
}
bool get_pos(point a,point b,point c){
    double modlenb=get_dis(a,b),modlenc=get_dis(a,c);
    vec vecb=get_vector(a,b),vecc=get_vector(a,c);
    double prolen=get_point_mul(vecb,vecc)/modlenb;
    return (prolen>=0&&prolen<=modlenb)?1:0;
}
double get_line_point(point a,point b,point c){
    if(get_pos(a,b,c)){
        double s=get_area(a,b,c);
        double h=s/get_dis(a,b);
        return h;
    }
    return min(get_dis(a,c),get_dis(b,c));
}
int get_direction(point a,point b,point c){
    vec vecb=get_vector(a,b),vecc=get_vector(a,c);
    double mulres=cross(vecb,vecc);
    return (mulres<=0)?1:0;
}
int n,q;
point p[20000];
void solve(){
    cin>>n>>q;
    for(int i=1;i<=n;i++){
        int x,y;cin>>x>>y;
        p[i].x=x,p[i].y=y;
        p[i+n]=p[i];
    }
    while(q--){
        int a,b,c,d;
        cin>>a>>b>>c>>d;
        int f=0;
        point cir={(a+c)*1.0/2,(b+d)*1.0/2};
        double r=get_dis({a,b},{c,d})/2;
        double ans=r*r/2;
        for(int i=n+1;i>=2;i--){
            if(!get_direction(p[i],p[i-1],cir)){
                f=1;break;
            }
        }
        if(!f){
            cout<<fixed<<setprecision(8)<<ans<<endl;continue;
        }
        double minn=1.0*0x3f3f3f3f3f3f3f;
        for(int i=1;i<=n;i++){
            double d=get_line_point(p[i],p[i+1],cir);
            minn=min(minn,d);
        }
        cout<<fixed<<setprecision(8)<<ans+minn*minn<<endl;
    }
}
int main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--){
        solve();
    }

}