Alphafold2模型以及代码解读（一）

AlphaFold是由DeepMind开发的一种革命性蛋白质结构预测方法，它在2020年的Critical Assessment of protein Structure Prediction (CASP)比赛中取得了令人瞩目的成绩，大幅提高了蛋白质三级结构预测的准确性。AlphaFold的成功在很大程度上归功于它的创新模型架构和它所使用的大量数据。

生物相关

首先阐述几个生物学相关的名词：

序列的contact map

蛋白质的contact map（接触图）是一种用于描述蛋白质三维结构中氨基酸残基间相互接触的图形表示方法。在这种表示中，蛋白质被简化为沿着其主链的一系列氨基酸残基，而接触图则显示了这些残基间的空间接近程度。具体来说，如果两个氨基酸残基在三维空间中的距离小于某个阈值（通常为一定的埃数，如8埃），则认为这两个残基之间存在接触。

接触图通常表示为二维方阵，其中的行和列代表蛋白质序列中的氨基酸残基，而方阵中的元素表示相应残基对是否接触。如果残基i和残基j之间存在接触，则矩阵中的对应元素（i,j）被标记（例如，设为1或其他表示接触的值），否则该元素表示为不接触（例如，设为0）。这样，接触图为蛋白质三维结构提供了一种简化但信息丰富的表示，有助于理解蛋白质如何折叠以及其结构如何影响功能。

在蛋白质结构预测和建模中，接触图是一个非常有用的工具。通过预测蛋白质序列的接触图，可以辅助重建其三维结构。近年来，随着深度学习技术的发展，一些算法（如AlphaFold）已能够以高准确度预测蛋白质的接触图，这对于解决结构生物学中的一些长期难题具有重要意义。通过从序列信息预测接触图，再从接触图推导出三维结构，这些方法显著提高了蛋白质结构预测的精度和效率。

MSA

MSA（Multiple Sequence Alignment，多序列比对）是生物信息学中的一种常用技术，用于将来自不同物种的同源蛋白质或核酸序列进行排列，以便在水平方向上对齐它们的相应位置。通过MSA，研究人员可以识别不同序列之间的相似性和差异性，发现进化上保守的区域，预测蛋白质的功能区域，以及推断物种间的进化关系。

在MSA中，序列被排列成一个矩阵形式，矩阵的每一行代表一个序列，每一列代表所有序列在该位置的核苷酸或氨基酸。为了最大化不同序列之间的相似性，可能需要在某些序列中插入空位（通常用破折号表示），以便对齐保守区域或具有相似功能的基序。MSA的目的是找到一种排列方式，使得被比较的序列在尽可能多的位置上相匹配，同时尽量减少引入的空位数量。

MSA是理解蛋白质结构和功能、研究基因的进化以及进行系统发育分析的重要工具。例如，通过比较不同物种的蛋白质序列对齐，研究人员可以识别出在进化过程中高度保守的氨基酸残基，这些残基通常对蛋白质的功能至关重要。此外，MSA也是许多生物信息学分析和预测方法的基础，包括基因注释、蛋白质结构预测以及功能位点的识别等。

进行MSA的工具和算法有很多，比如Clustal Omega、MAFFT和MUSCLE等，它们各有优势和特点，适用于不同大小和复杂度的数据集。

phylogeny

蛋白质的phylogeny（系统发育学）是指研究不同物种中蛋白质序列或结构的演化关系。通过比较这些蛋白质，科学家们可以推断它们的共同祖先，了解生物进化的路径，以及不同物种之间是如何分化的。蛋白质系统发育分析不仅可以揭示蛋白质家族的演化历史，还可以帮助预测蛋白质的功能，特别是在比较那些具有已知功能蛋白质序列或结构的物种时。

蛋白质系统发育分析的主要步骤：

1. 序列或结构的收集与比较： 首先，需要收集待研究的蛋白质序列或结构。这通常涉及对公共数据库的查询，如NCBI或UniProt等。然后，使用序列比对工具（如BLAST）或结构比对工具（如DALI）比较这些蛋白质，以识别它们之间的相似性和差异性。

2. 构建多序列比对： 将收集到的蛋白质序列进行多序列比对（MSA），如使用Clustal Omega或MAFFT等工具。这一步骤能够揭示序列之间的保守区域和可变区域，这些区域可能对蛋白质的功能至关重要。

3. 推断系统发育树： 基于多序列比对的结果，使用系统发育推断工具（如MEGA、PhyML或RAxML等）构建系统发育树。这些工具通常采用统计模型（如最大似然法或贝叶斯法）来推断物种之间的演化关系。构建的系统发育树能够反映不同蛋白质或物种之间的演化距离和谱系关系。

4. 分析和解释系统发育树： 分析系统发育树可以揭示蛋白质家族的演化模式，哪些蛋白质是密切相关的，以及它们可能的共同祖先是什么。此外，也可以通过系统发育树来预测某个蛋白质的功能，尤其是当它与已知功能的蛋白质密切相关时。

应用：

• 功能预测：通过与已知功能的蛋白质的比较，可以预测未知蛋白质可能的功能。
• 进化研究：系统发育分析有助于理解生命的演化过程，包括物种是如何分化和演化的。
• 保守区域和关键残基的识别：通过分析蛋白质的系统发育关系，可以识别在演化过程中保守下来的区域和残基，这些区域和残基往往与蛋白质的功能密切相关。

模型概括

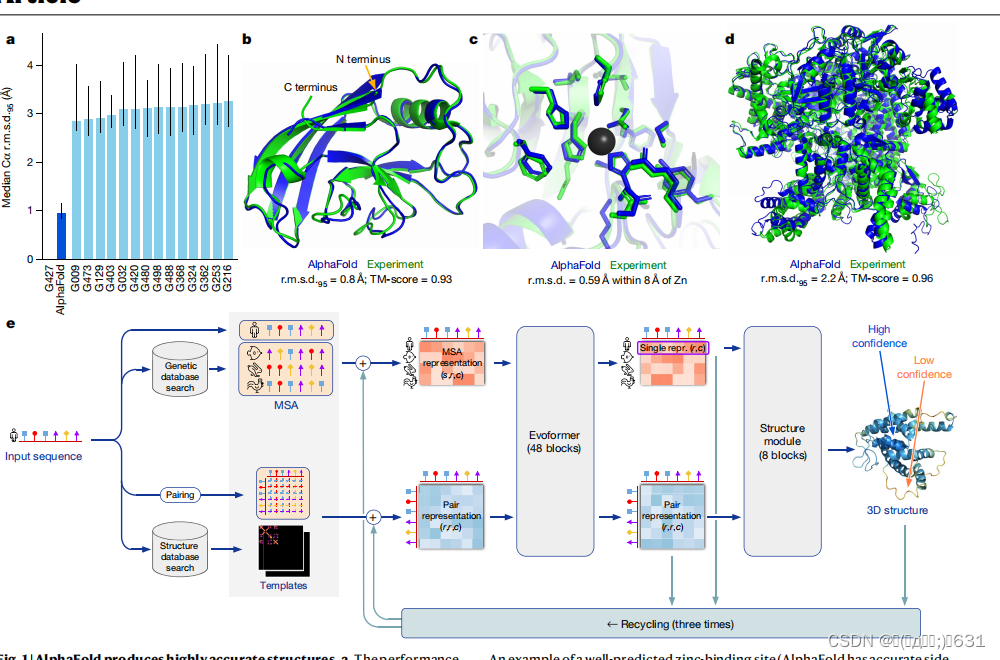
输入

在AlphaFold1的版本中，模型的输入主要包括多序列比对（MSA）数据和模板（Templates）数据，以及它们的来源数据库，具体如下：

1. 序列数据库:

   • UniRef90 使用JackHMMER进行搜索: UniRef90是一个大型的蛋白质序列数据库，其中包含了通过去除冗余数据压缩后的高质量蛋白质序列。通过对输入的蛋白质序列使用JackHMMER在UniRef90中进行搜索，可以生成MSA，从而帮助预测蛋白质的结构。
   • BFD (HHblits): BFD（Big Fantastic Database）数据库包括了大量的蛋白质序列，使用HHblits进行搜索可以获得更高质量的MSA，这对于预测缺乏已知结构的蛋白质尤其重要。
   • Mgnify 使用JackHMMER进行搜索: Mgnify是一个基于微生物组学数据的蛋白质序列数据库，它提供了大量来自环境样本的蛋白质序列，使用JackHMMER在此数据库中进行搜索可以扩展MSA的多样性，有助于提高预测的准确性。

2. 结构数据库:

   • PDB (用于训练): 蛋白质数据银行（Protein Data Bank，PDB）是一个包含了已知蛋白质三维结构数据的数据库，AlphaFold使用PDB中的数据进行训练，学习如何从MSA和模板信息预测蛋白质的结构。
   • PDB70聚类 (使用HHsearch): PDB70是基于PDB数据进行聚类后的数据库，其中的蛋白质结构被聚类到70%的相似性水平。使用HHsearch在PDB70中进行搜索可以找到与输入蛋白质序列最为相似的已知结构（模板），这些模板信息对于引导蛋白质结构的预测非常有用。

AlphaFold通过结合来自这些不同来源的数据，能够生成高质量的MSA和找到相关的结构模板，这两者是其预测蛋白质三维结构的关键输入。特别是，MSA的使用使得模型能够捕获进化信息，而模板的使用则提供了关于蛋白质可能结构的直接信息。这种综合利用序列和结构数据库的方法为AlphaFold模型提供了强大的预测能力。

 Evoformer

MSA row-wise gated self-attention with pair bias

1. Row-wise Self-Attention: 对于row-wise self-attention，我们的目标是为序列中的每个氨基酸计算一个上下文相关的表示。输入张量的形状是(s, r, c)，其中s是序列的数量，r是每个序列中的氨基酸的数量，c是嵌入的维度。

   对于每个序列（按行操作），我们计算Query（Q）、Key（K）和Value（V），然后进行点乘（Q * K^T）来获取注意力得分。这个得分代表了序列中各个残基之间的相似度。通过softmax函数对每行的得分进行归一化，然后使用这些归一化的得分对V进行加权求和，以获得每个位置的输出表示。

2. Gated Mechanism: 在门控机制中，我们使用一个线性层（通常是一个全连接层）来生成门控信号，然后通过sigmoid激活函数把这个信号转换为0和1之间的值。这个门控信号与自注意力的输出进行元素级别的乘法操作，从而实现对输出的控制。这与LSTM的输出门类似，LSTM的输出门决定了多少内部状态应该输出到下一状态。

3. Pair Bias: Pair bias是指在注意力得分或者最终输出上添加的偏置项，这个偏置项是基于残基对（pair）的。它允许模型为特定的残基对添加额外的信息或偏好，这有可能是基于氨基酸对之间的物理距离或其他生物学特性。Pair bias通常是一个可以学习的参数矩阵，其形状为(r, r)，表示残基对之间的相互作用强度。

import torch
import torch.nn.functional as F

def row_wise_self_attention(x):
    """
    x: 输入的MSA特征张量, 形状为 [s, r, c]
    返回: 经过row-wise self-attention计算后的特征张量
    """
    s, r, c = x.shape
    Q = x  # [s, r, c], 在这个简化版本中, 我们认为Q, K, V都是输入x
    K = x  # [s, r, c]
    V = x  # [s, r, c]
    
    # 计算Q和K的转置的点积, 形状为[s, r, r]
    attention_scores = torch.matmul(Q, K.transpose(-1, -2))
    
    # 应用softmax归一化
    attention_scores = F.softmax(attention_scores, dim=-1)
    
    # 和V相乘得到加权的特征表示
    output = torch.matmul(attention_scores, V)
    return output

def apply_gated_mechanism(x):
    """
    x: 输入的特征张量, 形状为[s, r, c]
    返回: 经过门控机制处理后的特征张量
    """
    gate = torch.sigmoid(x)  # 通过一个sigmoid激活函数，形状不变
    gated_output = x * gate  # 元素对应相乘
    return gated_output

def add_pair_bias(x, pair_bias):
    """
    x: 输入的特征张量, 形状为[s, r, c]
    pair_bias: 要添加的pair bias, 形状为[r, r]
    返回: 加入pair bias后的特征张量
    """
    # 假设pair_bias是可以广播到[s, r, r]的形状
    # 这里我们简化处理，直接在最后一个维度加上pair_bias
    # 实际中，可能需要根据实际情况调整如何合适地加入pair bias
    output = x + pair_bias.unsqueeze(0).unsqueeze(-1)
    return output

# 假设输入张量x的形状为[s, r, c]
x = torch.randn(10, 100, 64)  # 示例数据
pair_bias = torch.randn(100, 100)  # 示例pair bias

# 执行row-wise self-attention
x = row_wise_self_attention(x)

# 应用门控机制
x = apply_gated_mechanism(x)

# 加入pair bias
x = add_pair_bias(x, pair_bias)

# x现在包含了处理过的特征

MSA column-wise gated self-attention

为了构建不同列氨基酸之间的相关性，我们需要从一个不同的角度来考虑自注意力机制。这里的目标是捕捉序列（或列）之间的相关性，从而能够学习到蛋白质的phylogeny（系统发育树）信息。这种操作与row-wise操作相似，但我们需要在列（氨基酸位置）而非行（序列）上应用它。这将帮助模型理解不同位置的氨基酸如何共同演化。

在传统的自注意力机制中，我们计算的是序列内不同部分之间的关联。而在这里，我们需要将注意力转向序列的不同位置之间的相关性。以下是一个简化的实现方法：

列向自注意力机制

# 输入: X (s, r, c)
def column_wise_self_attention(X):
    # 首先，我们需要转置输入，使得列变为我们操作的主要维度
    # 为了操作的方便，我们暂时忽略序列数量s，只考虑单个序列（或者可以想象我们已经在batch维度上进行了操作）
    # X 现在的形状为 (r, c), 我们需要将其转置为 (c, r)
    X_transposed = X.transpose(1, 2)  # 维度转换为 (s, c, r)
    
    # 对转置后的X应用自注意力机制
    # 因为现在我们关注的是列之间的关联，所以Q, K, V的计算方式不变
    Q = linear(X_transposed)  # Q, K, V 使用相同或不同的线性变换
    K = linear(X_transposed)
    V = linear(X_transposed)
    
    attention_scores = softmax(Q @ K.transpose(-2, -1)) / K.size(-1)**0.5  # Q * K^T, 按列计算相似性，加入除以sqrt(d_k)进行缩放
    attention_output = attention_scores @ V  # Softmax(QK^T)V
    
    # 最后，我们可能需要将输出转置回原来的维度，以便与其他层兼容
    attention_output_transposed_back = attention_output.transpose(1, 2)  # 维度转换回 (s, r, c)
    
    return attention_output_transposed_back

这里的实现侧重于展示如何在列级别上应用自注意力，而这正是研究列间（即不同氨基酸位置间）相关性所需的操作。这个方法可以帮助模型学习到不同氨基酸位置如何协同演化，从而反映出蛋白质的phylogeny信息。

Outer product mean

两个氨基酸位置i和j分别通过一个线性层转换，然后它们的外积（在批处理中为点积）用于生成一个新的表示，这个表示最终被压缩并加到pair representation上。这个过程可以帮助捕获两个氨基酸位置之间的相互作用信息。

简单实现：

class OuterProductMean(nn.Module):
    def __init__(self, c_dim):
        super(OuterProductMean, self).__init__()
        # 定义两个线性层，用于将输入的氨基酸位置i和j转换到s,c的维度
        self.linear_i = nn.Linear(c_dim, c_dim)
        self.linear_j = nn.Linear(c_dim, c_dim)
        # 定义最后一个线性层，用于将外积平均后的向量转换回c的维度
        self.linear_final = nn.Linear(c_dim * c_dim, c_dim)

    def forward(self, amino_acid_i, amino_acid_j):
        # amino_acid_i 和 amino_acid_j 的维度都是 [s, c]
        
        # 首先，通过线性层转换
        transformed_i = self.linear_i(amino_acid_i)
        transformed_j = self.linear_j(amino_acid_j)
        
        # 计算外积，结果的维度为 [s, c, c]
        # 使用unsqueeze扩展维度，以便进行批量点积
        outer_product = torch.bmm(transformed_i.unsqueeze(2), transformed_j.unsqueeze(1))
        
        # 在s维度上求mean
        mean_outer_product = torch.mean(outer_product, dim=0)
        
        # 将矩阵拉平成向量
        flattened = mean_outer_product.view(-1)
        
        # 通过最后一个线性层
        output = self.linear_final(flattened)
        
        # 这里的output可以加到pair representation上
        return output

# 假设的维度
s, c = 10, 64  # s是序列长度，c是特征维度

# 创建模型实例
model = OuterProductMean(c_dim=c)

# 模拟输入数据
amino_acid_i = torch.randn(s, c)
amino_acid_j = torch.randn(s, c)

# 前向传播
output = model(amino_acid_i, amino_acid_j)
print(output.shape)  # 应该是 [c,]

OuterProductMean类首先通过两个独立的线性层处理两个输入向量（代表氨基酸位置i和j的特征），然后计算这两个向量的外积，并在批次维度上求平均。最后，将得到的平均外积矩阵拉平并通过另一个线性层转换，以生成最终的输出向量。这个输出向量的维度是[c,]，可以直接加到pair representation上。

Triangular attention

三角形不等式块在AlphaFold2架构中起着重要作用，它们利用生物学中的三角不等式原理来改进蛋白质结构预测的准确性。具体来说，这些块目的在于确保序列中任意两点间的预测距离符合实际的几何约束，即任意两点间的距离应小于或等于通过第三点间接连接时的路径长度。下面分别解释这两种机制的工作原理和意义。

 三角形乘法更新（Triangle Multiplicative Update）

三角形乘法更新块通过考虑通过中间残基k的所有可能路径来更新pair representation中任意两点i和j之间的表示。其核心思想是：

• 对于残基i和j，考虑通过所有可能的中间残基k的路径。
• 对于每一对(i,k)和(j,k)，将它们的embedding降维到更小的维度c，并施加门控机制。
• 然后对这对降维后的embedding进行Hadamard积（元素乘），累加所有通过k的路径。
• 通过层范数和进一步的门控来更新i和j之间的pair representation。

这一过程并不直接寻找最短路径，而是通过考虑所有可能的中间残基k并加权汇总这些路径，来隐式地约束i和j之间的距离。门控机制和层范数有助于筛选重要的路径和调整不同边的贡献，从而实现一种软约束的形式。

简单实现：

import torch
import torch.nn as nn
import torch.nn.functional as F

class TriangleMultiplicativeUpdate(nn.Module):
    def __init__(self, num_residues, channel_dim, gate_dim):
        super(TriangleMultiplicativeUpdate, self).__init__()
        self.num_residues = num_residues
        self.channel_dim = channel_dim
        self.gate_dim = gate_dim
        self.gate = nn.Linear(channel_dim, gate_dim)  # 门控机制

    def forward(self, pair_representations):
        updates = torch.zeros_like(pair_representations)
        
        # 执行对所有残基的迭代
        for k in range(self.num_residues):
            # 选择i-k和j-k的pair representations
            i_k = pair_representations[:, k, :, :]  # shape: (batch_size, num_residues, channel_dim)
            j_k = pair_representations[:, :, k, :]  # shape: (batch_size, num_residues, channel_dim)
            
            # 降维并应用门控
            i_k_gate = torch.sigmoid(self.gate(i_k))  # shape: (batch_size, num_residues, gate_dim)
            j_k_gate = torch.sigmoid(self.gate(j_k))  # shape: (batch_size, num_residues, gate_dim)
            
            # Hadamard乘积
            hadamard_product = i_k_gate * j_k_gate  # shape: (batch_size, num_residues, gate_dim)
            
            # 累加所有通过k的路径
            updates += hadamard_product
        
        # 层范数和门控更新
        updates = F.layer_norm(updates, normalized_shape=[self.num_residues, self.gate_dim])
        gated_updates = pair_representations * updates  # 可能需要另一个门控机制
        
        return gated_updates

# 假设pair_representations为(batch_size, num_residues, num_residues, channel_dim)形状的张量
pair_representations = torch.rand(2, 100, 100, 64)  # 示例输入数据，batch_size=2, num_residues=100, channel_dim=64
tmu_block = TriangleMultiplicativeUpdate(num_residues=100, channel_dim=64, gate_dim=32)
updated_pair_representations = tmu_block(pair_representations)

三角形自我注意（Triangle Self-Attention）

三角形自我注意块利用自注意力机制根据边的相对位置和长度来更新中心边的表示。其工作原理大致如下：

• 以中心边(i,j)作为查询（query），左边(i,k)作为键（key）和值（value）。
• 更新中心边（i,j）时，不仅考虑左边的信息，还将右边(j,k)的长度加入到点积亲和力（dot-product affinities）计算中，以考虑通过k点的间接路径。
• 同样，通过门控机制来调整中心边的表示。

这个机制允许模型考虑通过第三点k的间接路径对边(i,j)的贡献，以及如何根据这些间接路径来调整边(i,j)的表示。通过这种方式，模型可以更好地捕捉到蛋白质结构中的几何约束。

class TriangleSelfAttention(tf.keras.layers.Layer):
    def __init__(self, units):
        super(TriangleSelfAttention, self).__init__()
        self.units = units
        self.query_dense = tf.keras.layers.Dense(units)
        self.key_dense = tf.keras.layers.Dense(units)
        self.value_dense = tf.keras.layers.Dense(units)
        self.gate_dense = tf.keras.layers.Dense(1, activation='sigmoid')

    def call(self, inputs, edge_lengths):
        # inputs: [batch_size, num_edges, features]
        # edge_lengths: [batch_size, num_edges, num_edges] tensor with distances or lengths between edges

        query = self.query_dense(inputs)  # [batch_size, num_edges, units]
        key = self.key_dense(inputs)  # [batch_size, num_edges, units]
        value = self.value_dense(inputs)  # [batch_size, num_edges, units]

        # Compute dot-product attention
        attention_scores = tf.matmul(query, key, transpose_b=True)  # [batch_size, num_edges, num_edges]
        
        # Incorporate edge lengths into attention scores
        attention_scores += edge_lengths
        
        attention_weights = tf.nn.softmax(attention_scores, axis=-1)  # [batch_size, num_edges, num_edges]
        
        # Compute the updated values for each edge
        updated_values = tf.matmul(attention_weights, value)  # [batch_size, num_edges, units]
        
        # Use a gate to adjust the update
        gate = self.gate_dense(inputs)  # [batch_size, num_edges, 1]
        outputs = gate * inputs + (1 - gate) * updated_values  # [batch_size, num_edges, features]

        return outputs

# Example usage
batch_size = 1
num_edges = 3
features = 4
units = 5

# Simulate input data
inputs = tf.random.uniform((batch_size, num_edges, features))
edge_lengths = tf.random.uniform((batch_size, num_edges, num_edges))

# Instantiate and call the TriangleSelfAttention layer
triangle_self_attention = TriangleSelfAttention(units=units)
outputs = triangle_self_attention(inputs, edge_lengths)
print(outputs)

这两种机制都是通过软约束来实现三角不等式的，而不是硬性地寻找最短路径。这种设计允许模型保持灵活性和可微性，同时引入有助于提高预测准确性的几何约束。尽管这些机制在实现上较复杂，但它们对于AlphaFold2达到sota的表现至关重要。

 IPA (Invariant point attention)

不变点注意模块（IPA）：接着，不变点注意（Invariant Point Attention, IPA）模块将MSA嵌入、配对表示和骨架框架（backbone frames）整合在一起，以预测蛋白质的3D结构。这个模块能够考虑到氨基酸序列、它们之间的相互作用以及蛋白质的空间结构，从而提供了一个全面的信息视角来指导结构的预测。值得注意的是，即使在没有IPA的情况下，通过回收过程（reiterative refinement），AlphaFold2仍然能够准确地预测蛋白质结构。

Backbone update

这个步骤关键在于理解和表示蛋白质的三维结构。蛋白质由一串氨基酸序列组成，每种氨基酸都包含一个共有的骨架（由氨基-N、碳原子-Cα和羧基-C组成）及一个独特的侧链。在三维空间中，这些骨架元素的几何排列决定了蛋白质的结构和功能。

三角形表示 在AlphaFold等预测方法中，蛋白质骨架的每个氨基酸残基被表示为一个三角形，这有助于捕捉残基的局部结构。这个三角形有三个顶点：

• C-α原子：氨基酸残基的中心原子，连接着骨架的氨基和羧基，以及侧链。
• N原子：骨架的一个端点，组成氨基酸的氨基的一部分。
• C原子：骨架的另一个端点，组成氨基酸的羧基的一部分。

平移向量和旋转矩阵 对于每个残基，系统预测两个关键的几何变量：

• 平移向量：指的是从一个残基的C-α原子到下一个残基的C-α原子的空间位置的变化。这个向量说明了骨架在这两个点之间的线性移动。
• 旋转矩阵：描述的是一个残基的骨架相对于前一个残基的骨架如何旋转。代表了在空间中一个固定点绕一个轴的旋转。

结构更新 当系统预测出每个残基的平移向量和旋转矩阵后，就可以更新整个蛋白质的3D结构了。从第一个氨基酸残基开始，通过应用相应的平移和旋转，可以逐步构建出整个蛋白质的三维结构。这个过程从N端（氨基末端）到C端（羧基末端）连续进行，就像是把一串珠子串成一个三维的形状。

结构优化 得到初始的3D模型之后，还需要对结构进行优化，以确保它不仅在几何上合理，而且在物理和化学上也是稳定的。这通常涉及到模拟蛋白质在类似生物环境下的动力学行为，使用分子动力学模拟等方法对结构进行"放松"，以找到更加接近真实状态的最低能量构形。通过这种方式，预测的蛋白质结构可以更加精确地反映实际的生物分子形状。