编译原理实验（二）———— LL（1）分析法

置顶 于 2025-03-25 10:05:52 发布
阅读量2.2k 收藏 26
点赞数 55
分类专栏： 编译原理实验报告单合集 文章标签： 编译原理 c语言 算法 实验报告单
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_74326393/article/details/146495530
版权

一、实验目的

  1. 掌握LL(1)分析法的核心思想与实现流程，理解其作为非递归自顶向下分析方法的特点。
  2. 通过构造预测分析表和模拟分析过程，验证符号串i+i*i#是否符合给定文法，加深对FIRST集、FOLLOW集、SELECT集计算方法的理解。
  3. 探索LL(1)文法对左递归、公共前缀的消除要求，掌握文法等价变换方法。

二、实验题目

实验规定对下列文法，用LL（1）分析法对任意输入的符号串进行分析： 

（1）E::=TG

（2）G::=+TG

（3）G::=ε

（4）T::=FS

（5）S::=*FS

（6）S::=ε

（7）F::=(E)

（8）F::=i

若输入串为i+i*i# ，则输出为：

步骤分析栈剩余输入动作
1#Ei+i*i#E→TG，栈变为#GT
2#GTi+i*i#T→FS，栈变为#GSF
3#GSFi+i*i#F→i，匹配i，栈变为#GS
4#GS+i*i#S→ε，弹出，栈变为#G
5#G+i*i#G→+TG，栈变为#GT+
6#GT+i*i#匹配+，栈变为#GT
7#GTi*i#T→FS，栈变为#GSF
8#GSFi*i#F→i，匹配i，栈变为#GS
9#GS*i#S→FS，栈变为#GSF
10#GSF*i#匹配*，栈变为#GSF
11#GSFi#F→i，匹配i，栈变为#GS
12#GS#S→ε，弹出，栈变为#G
13#G#G→ε，弹出，栈变为#
14##分析成功

三、实验理论依据

1. LL(1)分析法核心概念

  • 基本思想：通过当前栈顶非终结符和输入符号，唯一确定产生式进行推导，无需回溯。
  • 关键集合：
    • FIRST(α) ：从α推导出的首终结符集合（含ε）。
    • FOLLOW(A) ：非终结符A后可能出现的终结符集合。
    • SELECT(A→α) ：FIRST(α)（若α不能推导出ε）或FIRST(α) ∪ FOLLOW(A)（若α可推导出ε）。
  • LL(1)文法条件：同一非终结符的所有候选式的SELECT集互不相交。

2. 分析表构造规则

非终结符输入符号产生式
Aa若a ∈ SELECT(A→α)，填入A→α

四、LL（1）分析法的设计

1. 验证文法为LL(1)文法

步骤1：计算FIRST集
符号FIRST集
E{ i, ( }
G{ +, ε }
T{ i, ( }
S{ *, ε }
F{ i, ( }
步骤2：计算FOLLOW集
符号FOLLOW集
E{ ), # }
G{ ), # }
T{ +, ), # }
S{ +, ), # }
F{ *, +, ), # }
步骤3：计算SELECT集
产生式SELECT集
E → T G{ i, ( }
G → + T G{ + }
G → ε{ ), # }
T → F S{ i, ( }
S → * F S{ * }
S → ε{ +, ), # }
F → ( E ){ ( }
F → i{ i }

验证：同一非终结符的候选式SELECT集无交集，满足LL(1)条件。

2. 构造预测分析表

非终结符i+*()#
EE→TGE→TG
GG→+TGG→εG→ε
TT→FST→FS
SS→εS→*FSS→εS→ε
FF→iF→(E)

五、实例代码+运行结果

1.实例代码（一）：
（1）源代码文件：
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

char A[20];       // 分析栈
char B[20];       // 输入串
char v1[] = "i+*()#";  // 终结符集合
char v2[] = "EGTSF";   // 非终结符集合

typedef struct {
    char origin;     // 产生式左部
    char array[5];   // 产生式右部
    int length;      // 右部长度
} Production;

Production C[5][6];  // 预测分析表 [非终结符][终结符]

// 初始化预测分析表
void initTable() {
    // 行索引：E(0),G(1),T(2),S(3),F(4)
    // 列索引：i(0),+(1),*(2),(3),)(4),#(5)
    
    // E行
    C[0][0] = (Production){'E', "TG", 2};   // i
    C[0][3] = (Production){'E', "TG", 2};   // (
    
    // G行
    C[1][1] = (Production){'G', "+TG", 3};  // +
    C[1][4] = (Production){'G', "^", 1};     // )
    C[1][5] = (Production){'G', "^", 1};     // #
    
    // T行
    C[2][0] = (Production){'T', "FS", 2};   // i
    C[2][3] = (Production){'T', "FS", 2};   // (
    
    // S行
    C[3][1] = (Production){'S', "^", 1};    // +
    C[3][2] = (Production){'S', "*FS", 3};  // *
    C[3][4] = (Production){'S', "^", 1};     // )
    C[3][5] = (Production){'S', "^", 1};     // #
    
    // F行
    C[4][0] = (Production){'F', "i", 1};    // i
    C[4][3] = (Production){'F', "(E)", 3};  // (
}

void printStack() {  // 输出分析栈
    printf("#");
    for(int i = strlen(A)-1; i >= 0; i--) {
        if(A[i] != '#') printf("%c", A[i]);
    }
    printf("\t\t");
}

void printInput() {  // 输出剩余输入串
    printf("%s", B);
    printf("\t\t");
}

int main() {
    char ch;
    int j = 0, b = 0, top = 0, step = 1;
    int finish = 0, flag = 0, l;
    
    initTable(); // 初始化预测分析表
    
    // 输入处理
    printf("请输入待分析的字符串（以#结尾）：");
    do {
        scanf("%c", &ch);
        if(strchr(v1, ch) == NULL && ch != '#') {
            printf("输入包含非法字符'%c'\n", ch);
            exit(1);
        }
        B[j++] = ch;
    } while(ch != '#');
    l = j;
    B[j] = '\0';
    
    // 初始化分析栈
    A[top] = '#';
    A[++top] = 'E';
    ch = B[0];
    
    printf("\n步骤\t分析栈\t\t剩余输入\t\t动作\n");
    printf("-----------------------------------------------------------\n");
    
    do {
        printf("%-4d\t", step++);
        printStack();    // 输出分析栈
        printInput();    // 输出剩余输入
        
        char x = A[top--]; // 弹出栈顶符号
        flag = 0;
        
        // 判断是否为终结符
        for(int i = 0; i < strlen(v1); i++) {
            if(x == v1[i]) {
                flag = 1;
                break;
            }
        }
        
        if(flag) { // 终结符处理
            if(x == '#') {
                printf("接受\n");
                finish = 1;
                break;
            }
            if(x == ch) {
                printf("匹配 %c\n", ch);
                // 移除已匹配字符
                memmove(B, B+1, strlen(B));
                ch = B[0];
            } else {
                printf("错误：栈顶为%c，输入为%c\n", x, ch);
                exit(1);
            }
        } else { // 非终结符处理
            int m = -1, n = -1;
            // 查找非终结符行坐标
            for(int i = 0; i < strlen(v2); i++) {
                if(v2[i] == x) {
                    m = i;
                    break;
                }
            }
            // 查找终结符列坐标
            for(int i = 0; i < strlen(v1); i++) {
                if(v1[i] == ch) {
                    n = i;
                    break;
                }
            }
            
            if(m == -1 || n == -1 || C[m][n].origin == '\0') {
                printf("错误：无可用产生式（%c遇到%c）\n", x, ch);
                exit(1);
            }
            
            Production prod = C[m][n];
            printf("用 %c→%s 推导\n", prod.origin, prod.array);
            
            // 压栈处理
            if(prod.array[0] != '^') { // 非空产生式
                for(int i = prod.length-1; i >= 0; i--) {
                    A[++top] = prod.array[i];
                }
            }
        }
    } while(!finish && top >= 0);
    
    return 0;
}
（2） 代码说明：

代码说明：

  1. 数据结构优化：

    • 分析栈A和输入串B使用字符数组实现
    • Production结构体存储产生式信息
    • 预测分析表C按非终结符和终结符顺序存储产生式

  2. 核心功能实现：

    • initTable()初始化符合文法的预测分析表
    • 栈操作使用数组模拟，支持逆序压栈操作
    • 输入合法性检查确保符号在终结符集合内
    • 详细的推导过程输出，包含步骤、栈状态、剩余输入和动作

  3. 错误处理：

    • 非法字符输入检测
    • 栈顶与输入符号不匹配处理
    • 预测分析表查不到产生式时的错误处理

  4. 界面优化：

    • 改进栈和输入串的显示格式
    • 添加推导动作的明确说明
    • 支持任意长度输入处理（需以#结尾）
（3）输出结果截图：

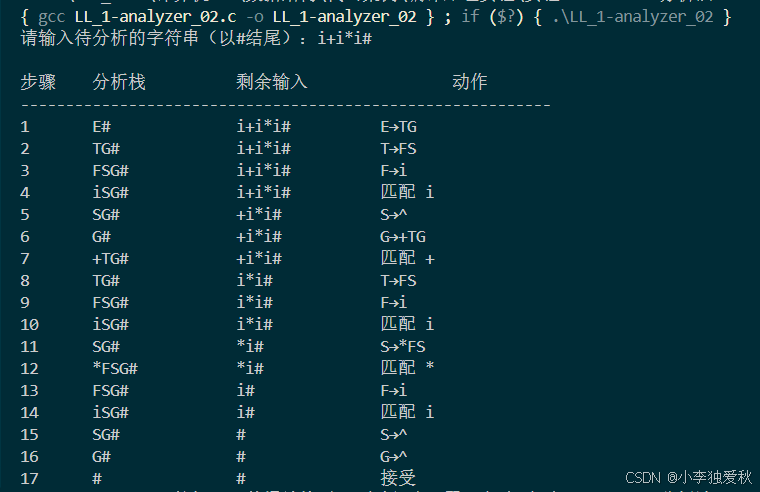
2.示例代码（二）[代码（1）加强版]：
（1）源代码文件：
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

char A[20];         // 分析栈
char B[20];         // 输入串
char v1[] = "i+*()#"; // 终结符集合
char v2[] = "EGTSF";  // 非终结符集合

typedef struct {    // 产生式结构体
    char origin;     // 左部符号
    char array[5];   // 右部符号
    int length;      // 右部长度
} Production;

Production C[5][6]; // 预测分析表 [非终结符][终结符]

// 初始化预测分析表
void initTable() {
    // 初始化所有表项为空
    for(int m=0; m<5; m++) {
        for(int n=0; n<6; n++) {
            C[m][n].origin = 'N'; // 'N'表示空项
        }
    }
    
    // E行
    C[0][0] = (Production){'E', "TG", 2};  // i
    C[0][3] = (Production){'E', "TG", 2};  // (
    
    // G行
    C[1][1] = (Production){'G', "+TG", 3}; // +
    C[1][4] = (Production){'G', "^", 1};   // )
    C[1][5] = (Production){'G', "^", 1};   // #
    
    // T行
    C[2][0] = (Production){'T', "FS", 2}; // i
    C[2][3] = (Production){'T', "FS", 2}; // (
    
    // S行
    C[3][1] = (Production){'S', "^", 1};  // +
    C[3][2] = (Production){'S', "*FS", 3};// *
    C[3][4] = (Production){'S', "^", 1};  // )
    C[3][5] = (Production){'S', "^", 1};  // #
    
    // F行
    C[4][0] = (Production){'F', "i", 1};  // i
    C[4][3] = (Production){'F', "(E)", 3};// (
}

// 输出分析栈
void printStack(int top) {
    for(int a = top; a >= 0; a--) {
        printf("%c", A[a]);
    }
    printf("\t\t");
}

// 输出剩余输入串
void printInput(int b, int l) {
    for(int j = b; j < l; j++) {
        printf("%c", B[j]);
    }
    printf("\t\t");
}

int main() {
    char ch;
    int j = 0, b = 0, top = 0, step = 1;
    int finish = 0, l;
    
    initTable(); // 初始化预测分析表
    
    // 输入处理
    printf("请输入待分析的字符串（以#结尾）：");
    do {
        scanf("%c", &ch);
        if(strchr(v1, ch) == NULL) {
            printf("输入包含非法字符'%c'\n", ch);
            exit(1);
        }
        B[j++] = ch;
    } while(ch != '#');
    l = j;
    
    // 初始化分析栈
    A[top] = '#'; 
    A[++top] = 'E'; // 初始符号入栈
    
    printf("\n步骤\t分析栈\t\t剩余输入\t\t动作\n");
    printf("-----------------------------------------------------------\n");
    
    do {
        printf("%-4d\t", step++);
        printStack(top);     // 输出分析栈
        printInput(b, l);    // 输出剩余输入
        
        char x = A[top--]; // 弹出栈顶符号
        
        // 判断是否为终结符
        int isTerminal = 0;
        for(int i = 0; i < strlen(v1); i++) {
            if(x == v1[i]) {
                isTerminal = 1;
                break;
            }
        }
        
        if(isTerminal) { // 终结符处理
            if(x == '#') {
                printf("接受\n");
                finish = 1;
                break;
            }
            if(x == B[b]) {
                printf("匹配 %c\n", x);
                b++; // 移动到下一个输入符号
            } else {
                printf("错误：栈顶为%c，输入为%c\n", x, B[b]);
                exit(1);
            }
        } else { // 非终结符处理
            int m = -1, n = -1;
            // 查找非终结符行号
            for(int i = 0; i < strlen(v2); i++) {
                if(v2[i] == x) {
                    m = i;
                    break;
                }
            }
            // 查找终结符列号
            for(int i = 0; i < strlen(v1); i++) {
                if(v1[i] == B[b]) {
                    n = i;
                    break;
                }
            }
            
            if(m == -1 || n == -1 || C[m][n].origin == 'N') {
                printf("错误：无可用产生式（%c遇到%c）\n", x, B[b]);
                exit(1);
            }
            
            Production prod = C[m][n];
            printf("%c→%s\n", prod.origin, prod.array);
            
            // 逆序压栈（空产生式不压栈）
            if(prod.array[0] != '^') {
                for(int i = prod.length-1; i >= 0; i--) {
                    A[++top] = prod.array[i];
                }
            }
        }
    } while(!finish);
    
    return 0;
}
（2）代码改进说明：

  1. 数据结构优化

    • 使用二维结构体数组C[5][6]存储预测分析表
    • 增加origin字段验证表项有效性
    • 使用字符'N'标记空表项

  2. 核心逻辑增强

    • 动态计算输入串长度l
    • 使用双指针b和top分别跟踪输入位置和栈顶
    • 改进栈打印逻辑，正确显示符号顺序

  3. 错误处理完善

    • 非法字符立即终止程序
    • 栈顶与输入符号不匹配时显示详细信息
    • 查表失败时显示具体符号组合

  4. 界面优化

    • 添加对齐格式控制符%-4d保持表格整齐
    • 动作列明确显示推导或匹配操作
（3）输出结果截图：

六、实验总结

1. 核心收获

  • 文法构造：需确保无左递归且SELECT集无冲突，否则需通过提取左因子、消除左递归进行等价变换。
  • 分析表驱动：通过预测分析表实现确定性的推导路径，避免回溯。
  • 效率与限制：LL(1)分析法时间复杂度为O(n)，但对文法要求严格，无法处理二义性文法。

2. 改进方向

  • 错误处理：可增加同步符号集（如FOLLOW集）实现错误恢复，跳过无效符号继续分析。
  • 扩展性：结合递归下降法实现更复杂的语义分析。
编译原理实验二——LL(1)分析法
wyk_3201864554的博客
04-20 265
学习用
编译原理LL(1)详解
weixin_34272308的博客
05-30 1230
前段时间为了做编译器，猛啃了一下编译原理。语法分析部分用的是比较简单上手的LL(1), 自认为LL(1)的理论部分理解得不错，在这里写出来跟大家share一下。 关于什么是LL(1)，就不赘述了，书上也说得很清楚，就是从左向右扫描输入，然后产生最左推导(就是每次都把最左边的非终结字符用产生式代替)。 (一)为什么我们需要First集合 比如有产生式 A-> + T | - P , 当我...
编译原理的语法分析——LL(1)分析表的实现.docx
12-04
LL（1）语法分析程序、自顶向下语法分析判断LL（1）文法的方法、文法等价变换、LL(1)分析表的构造、对某一输入串的分析过程的理解，本次实验的LL(1)文法为表达式文法： E→E+T | T T→T*F | F F→i | (E)
河北工业大学编译原理实验二——语法分析程序设计与实现
最新发布
m0_53240771的博客
07-04 1894
前言：本文是河北工业大学（Hebut）计算机科学与技术专业编译原理的实验报告。公开实验报告是为了传承当时做实验前辈们的帮助，也是希望大家可以共同学习。慎抄，或者不建议抄袭！ 实验二 语法分析程序设计与实现 一、实验目的 任选一种有代表性的语法分析方法，如算符优先法、递归下降法、预测分析法、LR分析法等，通过设计、编制、调试实现一个典型的语法分析程序，对实验一所得扫描器提供的单词序列进行语法检查和结构分析，实现并进一步掌握常用的语法分析方法。 二、基本实验内容与要求 选择对各种常见高级程序设计语言都较为通
编译原理实验（二）——LL（1）文法语法分析
热门推荐
antRain的博客
11-09 1万+
编译原理实验（二）——LL（1）文法语法分析实验要求参考程序程序输入说明实验结果截图 实验要求 根据LL(1)分析法编写一个语法分析程序 直接输入根据已知文法构造的分析表M;对于输入的文法和符号串，所编制的语法分析程序应能正确判断此串是否为文法的句子，并要求输出分析过程。 参考程序 #include <iostream> #include <string> #include...
【编译原理】 实验三 LL(1)分析法(LL1分析表的自动生成) 完整代码
zombotany的博客
07-10 4916
1.实现LL(1)分析算法 2.输入：教材中的算术表达式文法；待分析的语句（如i+i*i） 3.输出：语句的分析过程（参见ppt例题） 4.要求：LL(1)分析表程序自动生成。如果使用已知的分析表，实验分数会降低。 二、实验目的 通过设计、编制、调试一个具体的文法分析程序，深入理解LL(1)预测分析法的基本分析原理，理解FIRST集、FOLLOW集的构造方法并对其加以实现，构造LL(1)预测分析表并利用分析表对语句、文法进行分析。 三、实验分析 书中算术表达式文法示例如下： ——————————————
LL(1)文法分析代码
05-17
c语言写的 已知文法，求出分析表 分析字符串是否是文法的句型。不是原创，经过修改正确 在C++编译器中运行
LL(1)文法分析代码大全
05-13
你想做LL(1)文法分析吗？ 你还没有写好代码吗？ 老师是不是在后面追着你要作业呢？ 来下载这个吧！ 有了它，你的LL(1)文法分析肯定过关！
编译原理_LL(1)
frog77
11-04 249
因为过去几节课比较摸鱼，到了这节已经有好多听不懂了。 所以试着学一下LL(k) (突然学会了点LATEXL^AT_EXLATE​X正好试试看） 传送门 Preparations：Preparations：Preparations： $1.context-free\ grammar \ 上下文无关文法 $ 网上的很多概念看起来比较费力，引用知乎上的回答： 上下文无关文法就是说这个文法中所有的产生式左边只有一个非终结符 比如： S→aSbS \rightarrow aSbS→aSb S→abS \rightar
编译原理——LL(1)文法
hgeeacker的博客
04-23 331
提左因子疑问 https://bbs.csdn.net/topics/392144801?page=1 代码 https://blog.csdn.net/dianlixiong9237/article/details/102041983?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-7&a...
编译原理LL(1)语法分析
07-09
本程序是一个用C语言编写的一个简单的LL(1)语法分析器，简单实用。
LL(1)的语法分析程序
01-11
编译原理课程设计项目，带报告 根据LL(1)分析法编写的语法分析程序: (1)输入已知文法，由程序自动构造文法的分析表M。 (2)所开发的程序可适用于不同的文法和任意输入串，且能判断该文法是否为LL(1)文法。 (3)对于输入的文法和符号串，正确判断此串是否为文法的句子，输出分析过程。 (4)可消除左递归左公因子 图形界面良好 可分析如下产生式集合（空字用‘@’表示） "E->E+T|T,T->T*F|F,F->i|(E)"; "S->ME,E->+ME|@,M->FT,T->*FT|@,F->i|(S)"; "S->AB,S->bC,A->@,A->b,B->@,B->aD,C->AD,C->b,D->aS,D->c";"S->AB|b,A->Sm,B->eA";
LL（1）分析
06-15
这是我写的LL1文法分析，主要是为了完成平时编译的实验报告
LL（1）语法分析器
12-19
LL（1）语法分析器，用Skinmagic做界面，VC++，用Boost库正则式来判断输入是否正确。
LL(1)语法分析程序
07-16
此程序能够检测任意文法是否是LL(1)文法，能求出文法中所有非终结符的First集、Follow集以及所有产生式的SELECT集。对于是LL(1)的文法，能够自动给出预测分析表。可以输入字符串，分析字符串是否为文法的句子，并给出分析过程。 程序采用MFC基于对话框的设计方法，界面美观，操作方便。
编译原理实验报告LR(1)分析法.doc
05-11
《编译原理实验报告——LR(1)分析法》 在计算机科学中，编译原理是一门关键的课程，它涉及到计算机程序如何被转换为机器可执行的形式。LR(1)分析法是编译器设计中的一种重要的语法分析技术，主要用于处理上下文无关...
编译原理语法分析——LL(1)分析表的实现.pdf
07-10
《编译原理》课程中的语法分析是编译过程的关键部分，而LL(1)分析法是一种广泛应用的自左向右、最左推导、仅使用一个输入符号预测的语法分析方法。LL(1)分析表的实现是实现编译器语法分析阶段的重要任务。 在编译器...
编译原理LL(1)预测分析法JAVA实现
06-21
1、项目开发工具为MyEclipse2014 2、使用了Struts2框架作为控制层 3、HTML5图形用户界面 4、JAVA语言写后端 该项目完成的功能有：自动消去规则左递归；自动计算出First、Follow集；自动构造预测分析表；可输入句子...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

小李独爱秋

你的鼓励将是我加更的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值