树的名词解释
树的平均运行时间是O(longN),对于大量数据,非常常用。

每棵树有N个结点node,N-1个边edge。
没有孩子的结点——树叶
A——根
有孩子的结点——父亲
有相同父亲的结点——兄弟
深度和高度
深度:结点的深度=根到该结点唯一路径的长(从该结点往上数到根)
高度:该结点到一片树叶最长路径的长(从该结点往下数)
根的深度=0
E的深度=1,高度=2
A的深度=0,高度=3
一棵树的深度=这棵树的高
树的实现
定义树的结点

每个结点都装着指向下一个孩子的指针,和指向他的兄弟的指针。
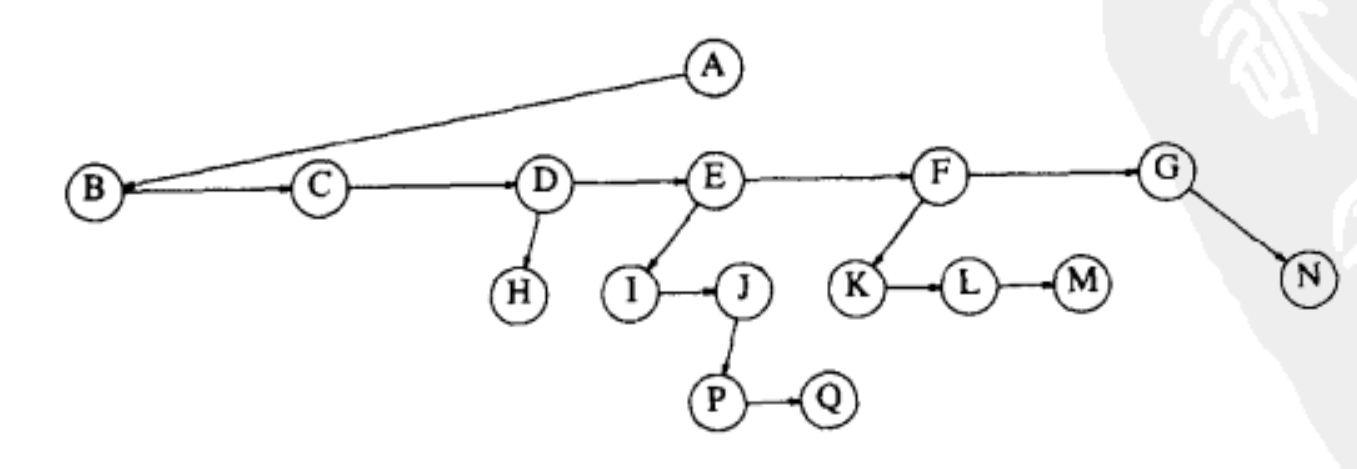
二叉树binary tree
每个结点不能有多于两个孩子的树——二叉树
ps: 所有的树都可以转化成二叉树
二叉树的性质

第i层最多的结点个数为:2^(i-1)
深度为k的二叉树最多的结点个数为:2^(k+1)-1
注意:根节点深度为0
完全二叉树和满二叉树
满二叉树一定是完全二叉树,且结点个数为:2^(k+1)-1
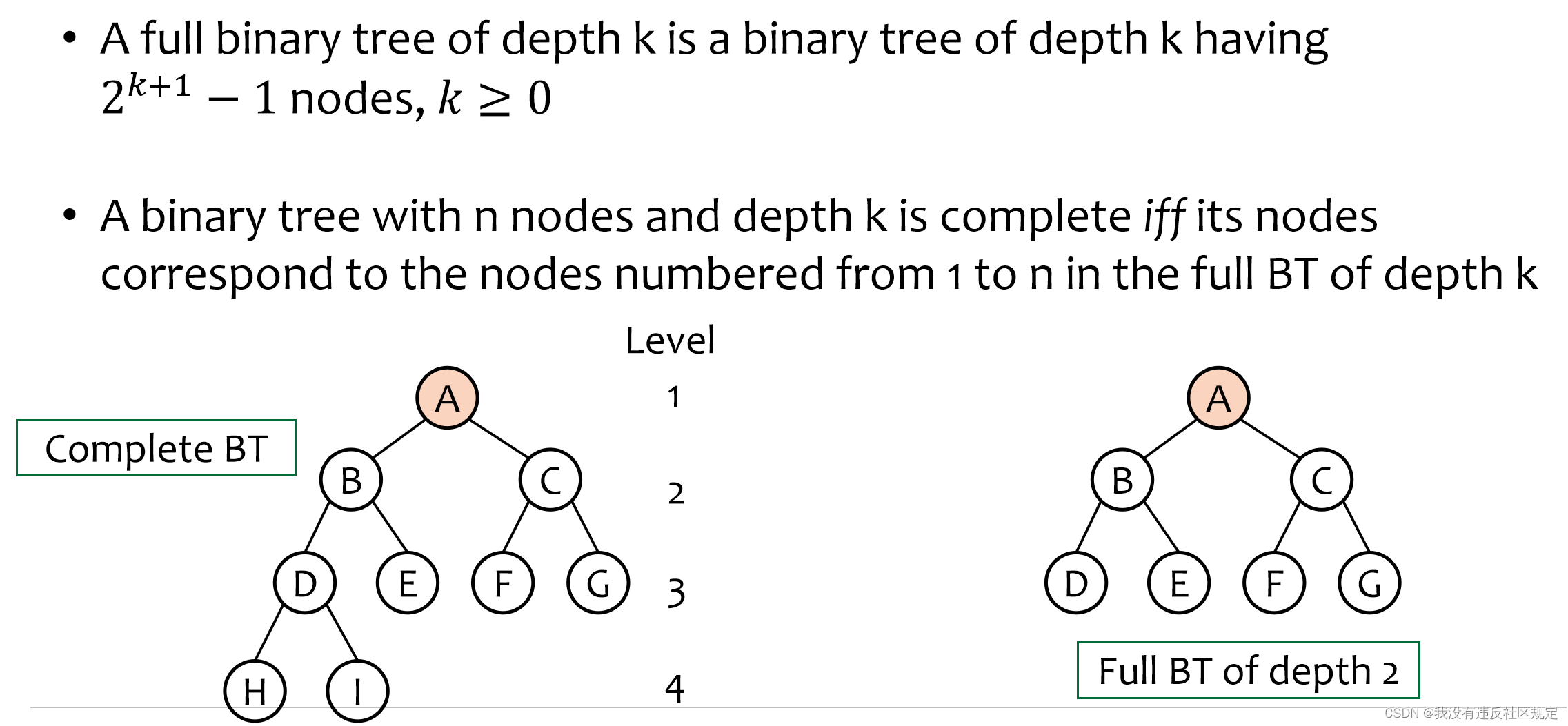
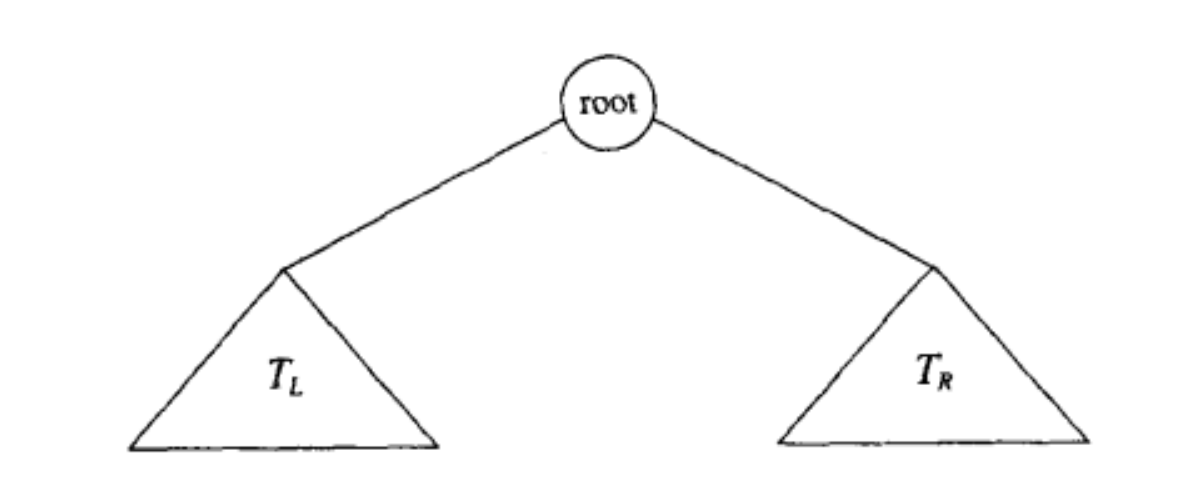
对于满二叉树,结点的序号有如下性质:

据此可以找到某个结点的parent,或者left and right child。
二叉树结点声明

typedef struct TreeNode
{
char data;
TreeNode *left;
TreeNode *right;
}Node,*root,*position ;//Node是结点的别名,root是指向根节点的指针,position是指向某个结点的指针
遍历一棵二叉树(BT)
广度优先bfs
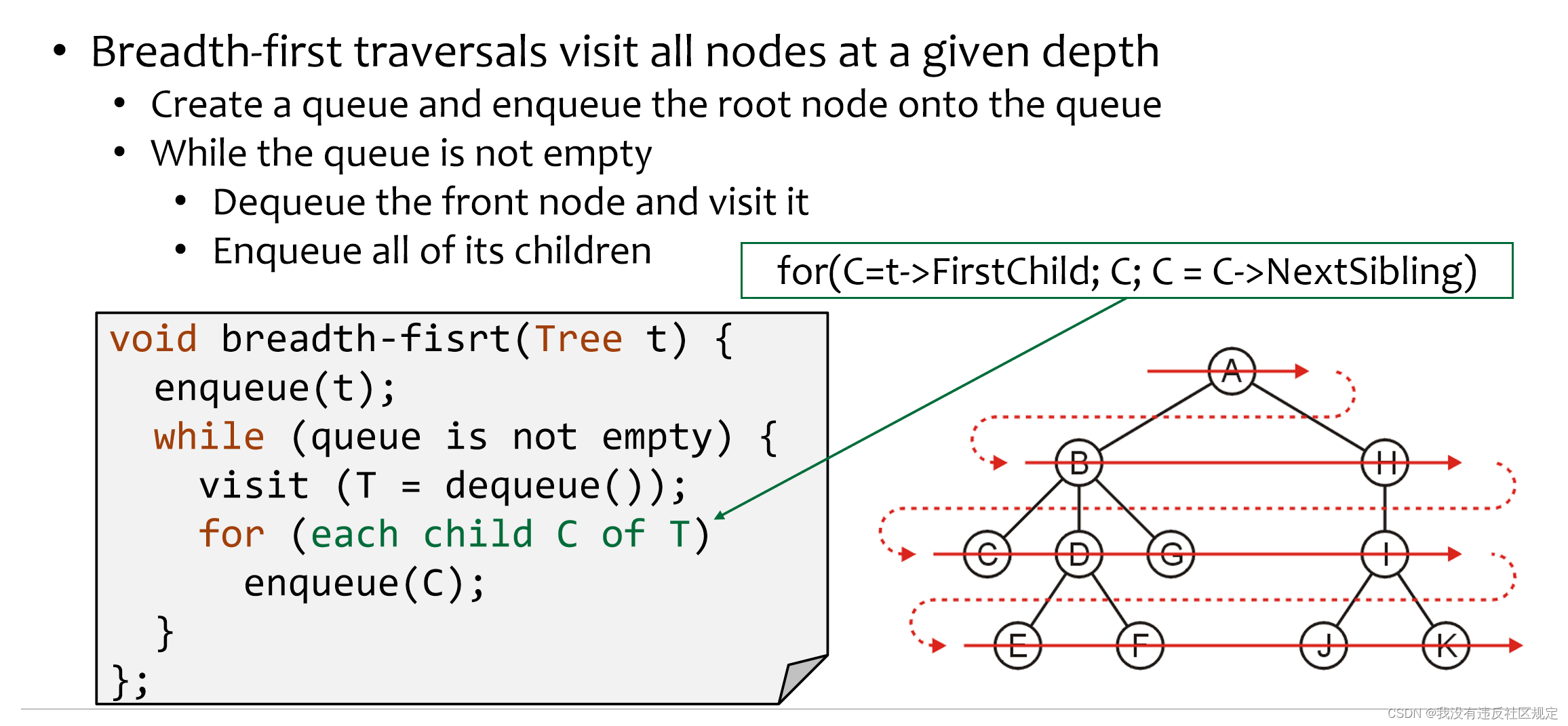
队列实现层次遍历
void bfs(Tree root)//广度优先
{
queue<Tree> t;//一个存放指针的队列,每个Tree指针指向一个结点
t.push(root);
while(!t.empty())
{
root=t.front();
t.pop();
cout<<root->data;
if(root->left)
t.push(root->left);
if(root->right)
t.push(root->right);
}
}
深度优先dfs
先序遍历
先处理某个结点,再处理他的孩子。
// Pre-order Traversal
void preorder(Tree T){
if(T != NULL){
visit(T);//先访问根节点
preorder(T->lchild);//再访问左结点
preorder(T->rchild);//最后访问右结点
}
return;
}
中序遍历
对于二叉树,先处理左孩子,然后处理这个结点,然后处理右孩子。
// In-order Traversal
void midorder(Tree T){
if(T != NULL){
midorder(T->lchild);//先访问左结点
visit(T);//再访问根结点
midorder(T->rchild);//最后访问右结点
}
return;
}
非递归版(栈实现)
// In-order non recursive
// go until find the start node for in-order visit
BiTreeNode* goL(BiTree t, Stack& S){
if (t == NULL) return NULL;
while (t->Left) {
S.push(t);
t = t->Left;
}
return t;
}
void iter_inorder(Bitree T) {
S = new Stack();
BiTreeNode* t = goL(T, S);
while(t) {
visit(t->Element);
if (t->Right) // find the start node in right substree
t = goL(t->Right, S);
else if (!IsEmpty(S))
t = S.pop();
else
t = NULL;
}
}
后序遍历
先处理完所有的孩子,再处理这个结点。
// Post-order Traversal
void postorder(Tree T){
if(T != NULL){
postorder(T->lchild);//先访问左结点
postorder(T->rchild);//再访问右结点
visit(T);//最后访问根节点
}
return;
}
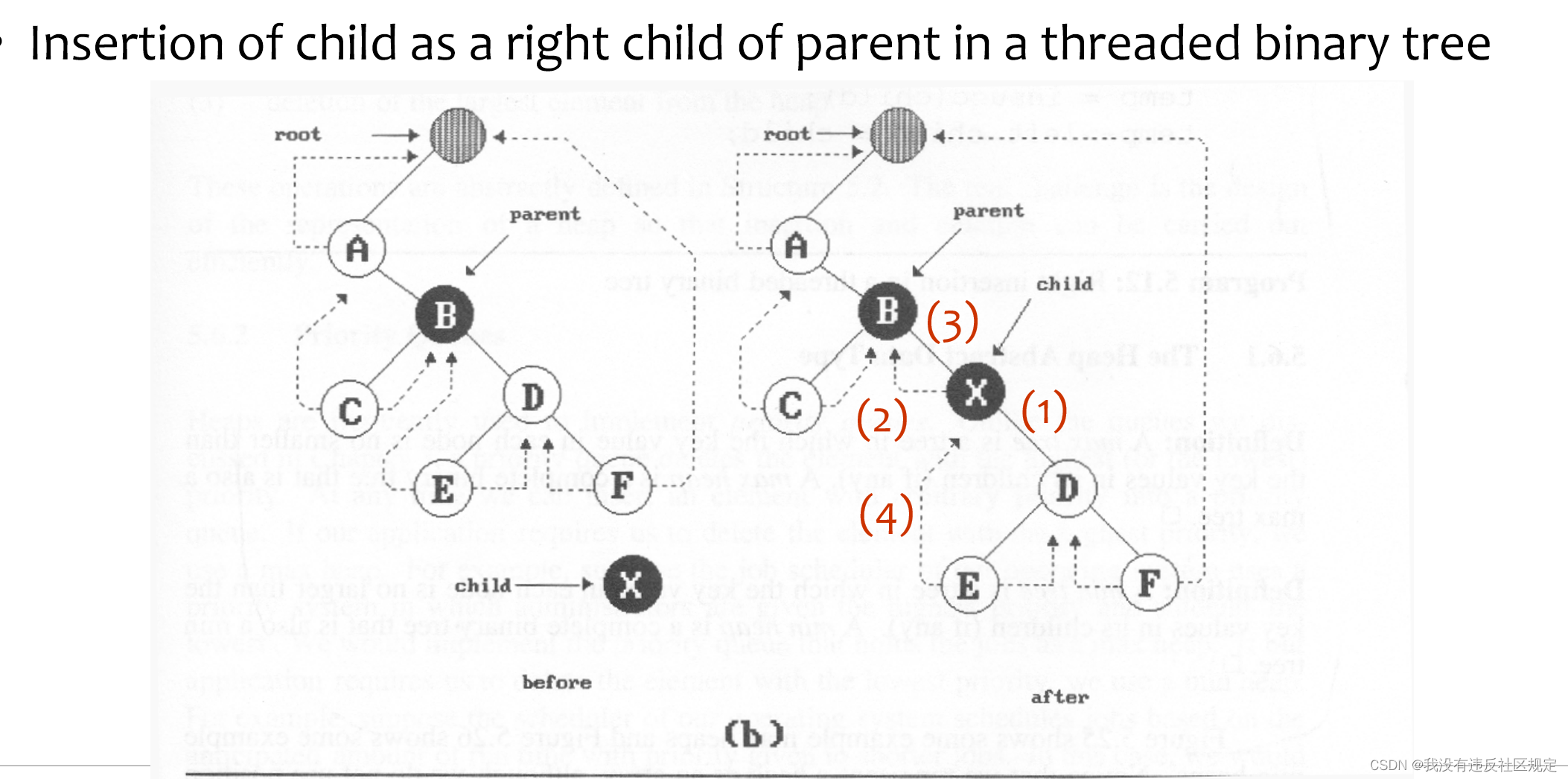
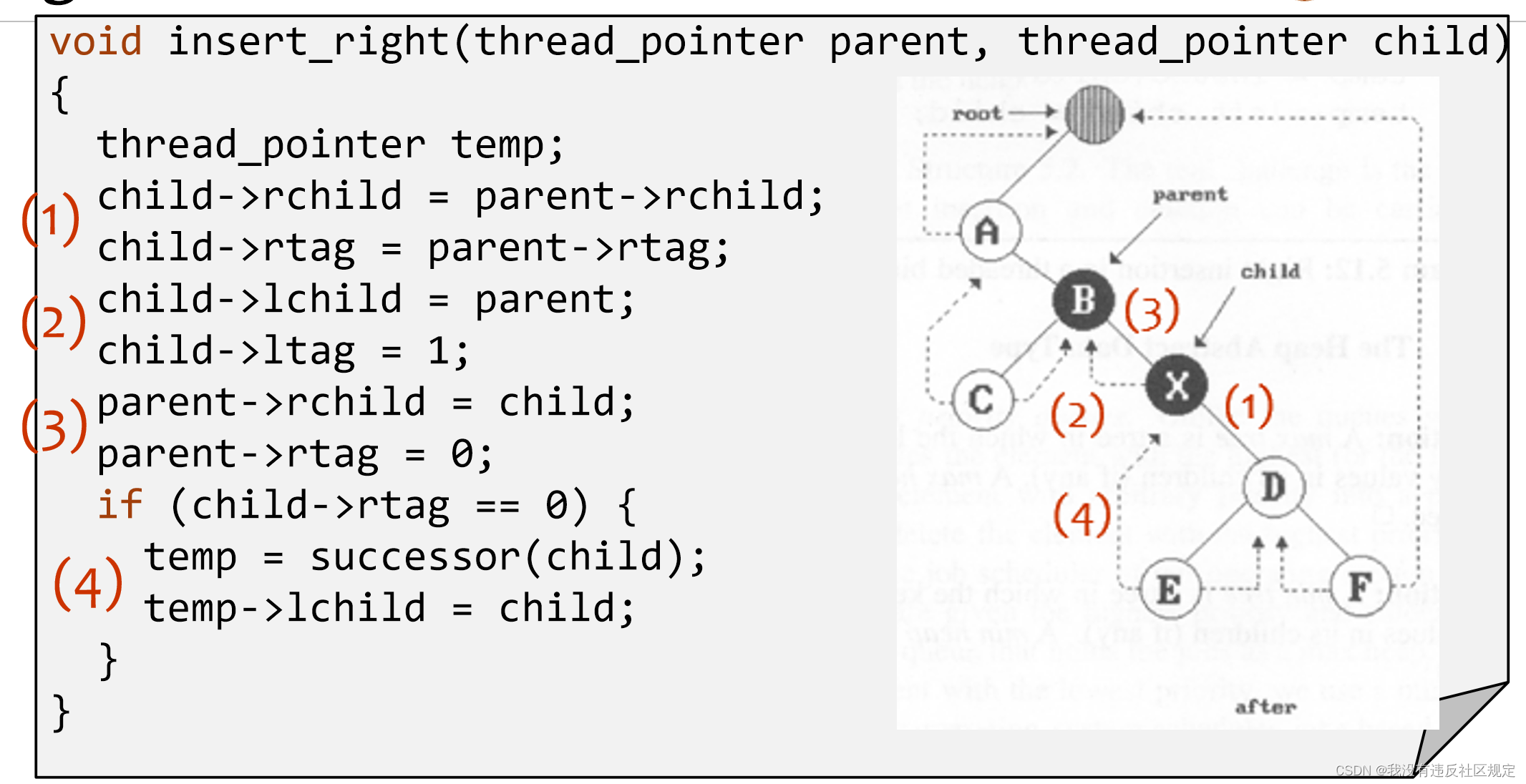
特殊二叉树——Threaded Binary Trees
线程二叉树是一种特殊的二叉树,它通过在某些节点上添加额外的指针来表达树中的线程关系。这些指针可以指向树中的其他节点,从而将一些节点连接起来形成线程。
根据指针线程化的方式不同,线程二叉树可以分为单线程二叉树和多线程二叉树。在单线程二叉树中,每个节点的左子节点或右子节点只有一个被线程化,而在多线程二叉树中,一个节点的左子节点和右子节点都可以被线程化。
需要注意的是,线程二叉树只是一种表达方式,它并不改变树中的节点之间的关系。换句话说,无论是使用普通的二叉树表示方式还是使用线程二叉树表示方式,树中节点之间的关系都是相同的。
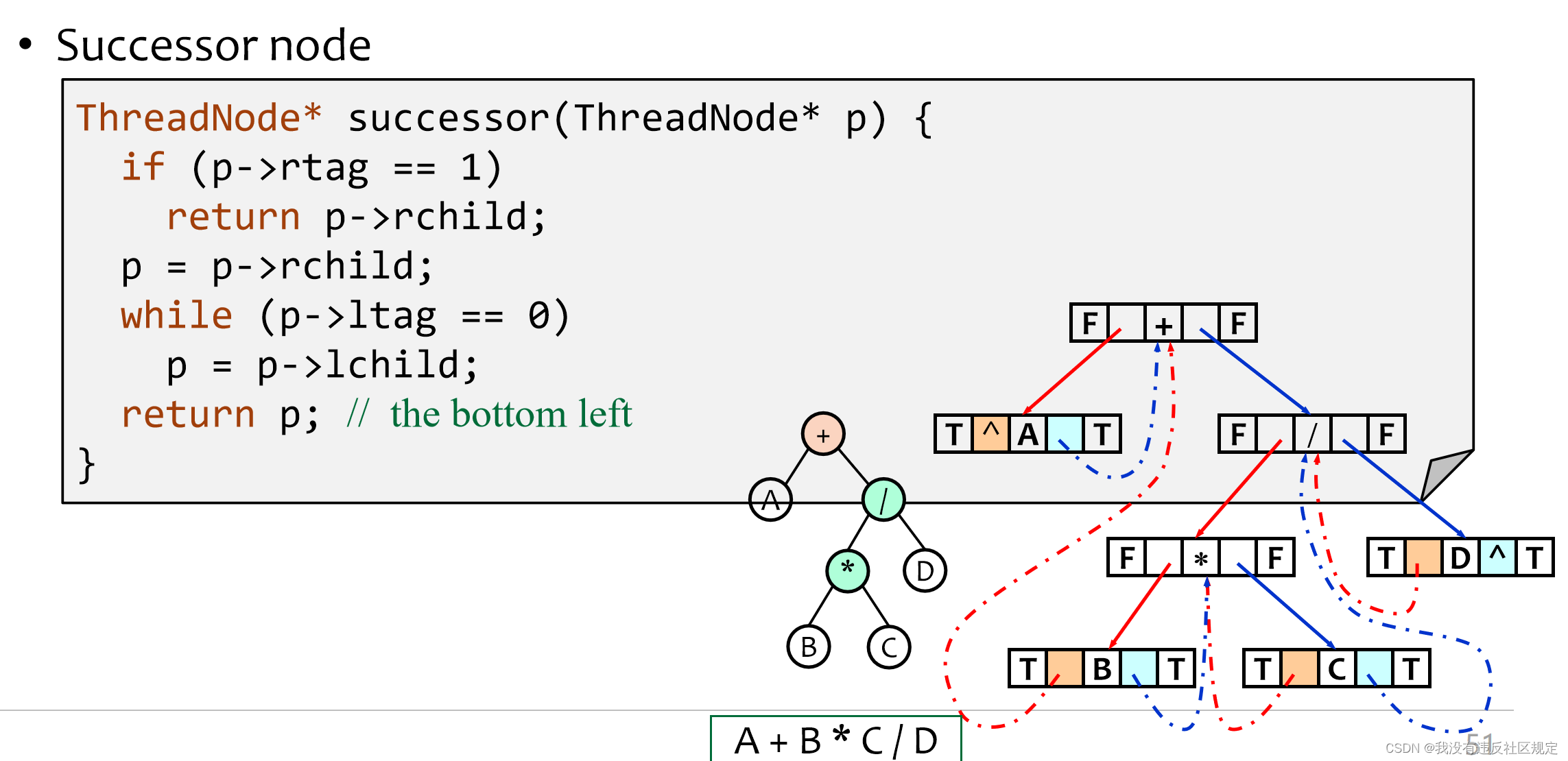
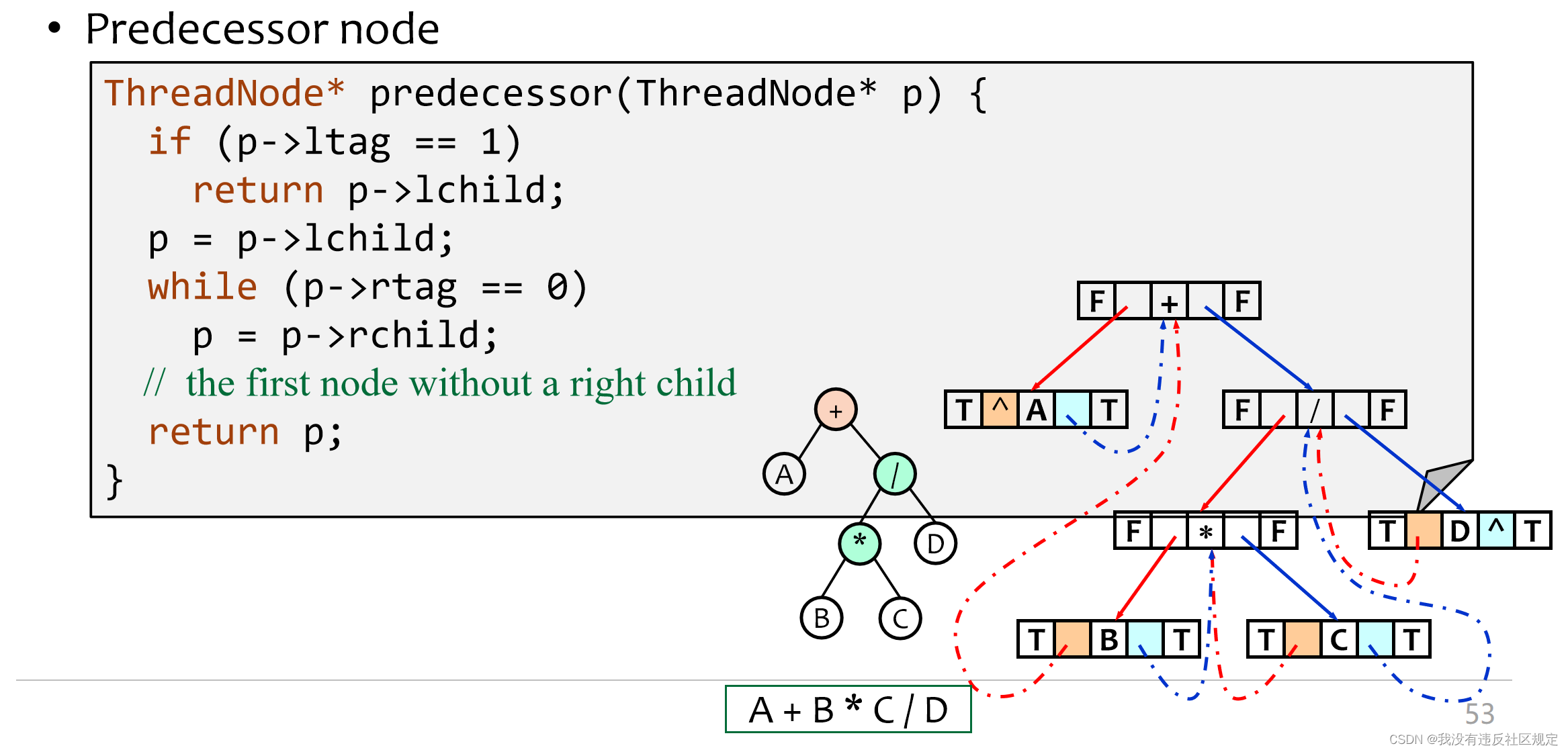
总之,线程二叉树是为了不浪费一些空指针,让他们指向某些successor and predecessor,使得后续操作更方便。
inorder

declaration

每个结点的左结点或右结点都被用来存储前驱结点或后序结点的信息,这样遍历二叉树时就不需要用栈或递归,大大提高了效率和空间。
// main method
void CreateThread( BiThrTree& t) {
ThreadNode* pre = NULL;
if (t != NULL) {
InThread(t, pre);
// the rtag of the last node
pre->rtag = 1;//前驱结点的右标记为1,表明是唯一的前驱
}
}
// pre pointer points to the in-order predecessor of t
void InThread(BiThrTree& t, ThreadNode* &pre) {
if (t != NULL) {
// Thread the left subtree
InThread(t->lchild, pre);
// Build predecessor thread of current node
if (t->lchild == NULL) {
t->lchild = pre;
t->ltag = 1;
}
// Build successor thread of pre node
if (pre && pre->rchild == NULL) {
pre->rchild = t;
pre->rtag = 1;
}
pre = t;
// Thread the right subtree
InThread(t->rchild, pre);
}
}

二叉树举例
(1)表达式树
树叶是操作数,其他结点是操作符。

中缀表达式:中序遍历得到

后缀表达式:后序遍历得到
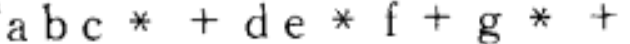
前缀表达式:前序遍历得到
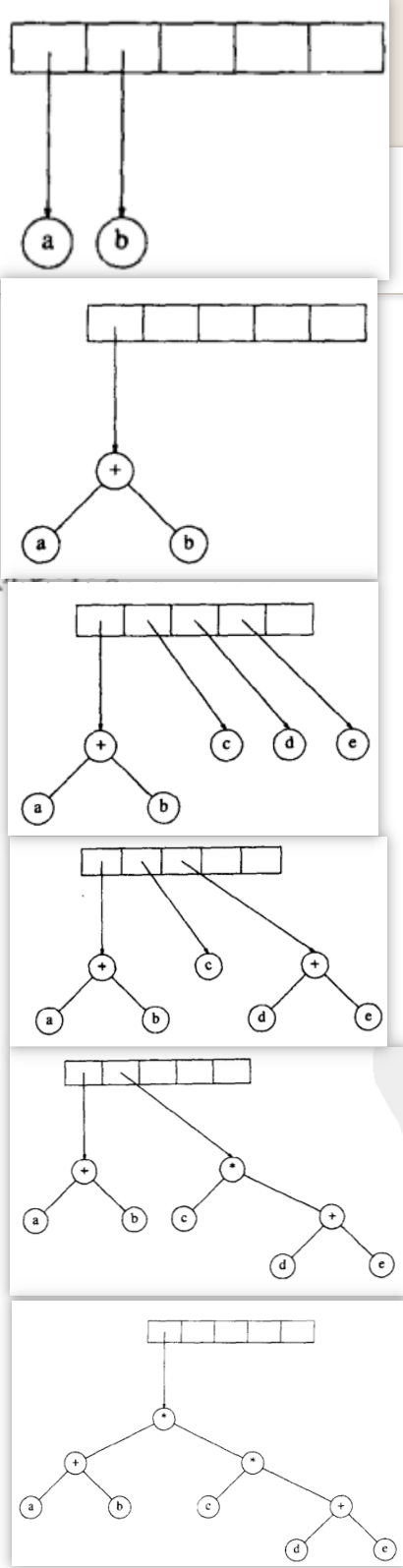
构造一棵表达式树
创建一个栈,读入数据:
如果是操作数,创建一个单点树,把指向他的指针压入栈。
如果是操作符,弹出栈中的两个指向操作数的指针,并把该操作符作为根。
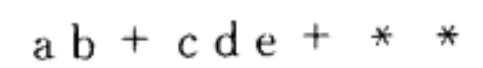
(2)查找树binary search tree (BST)
- 查找树的性质:
左子树的关键字值 < 该结点的关键字值
即:采用了某种统一的方式排序
通常会采用递归的方式来编写
查找树的操作
函数声明
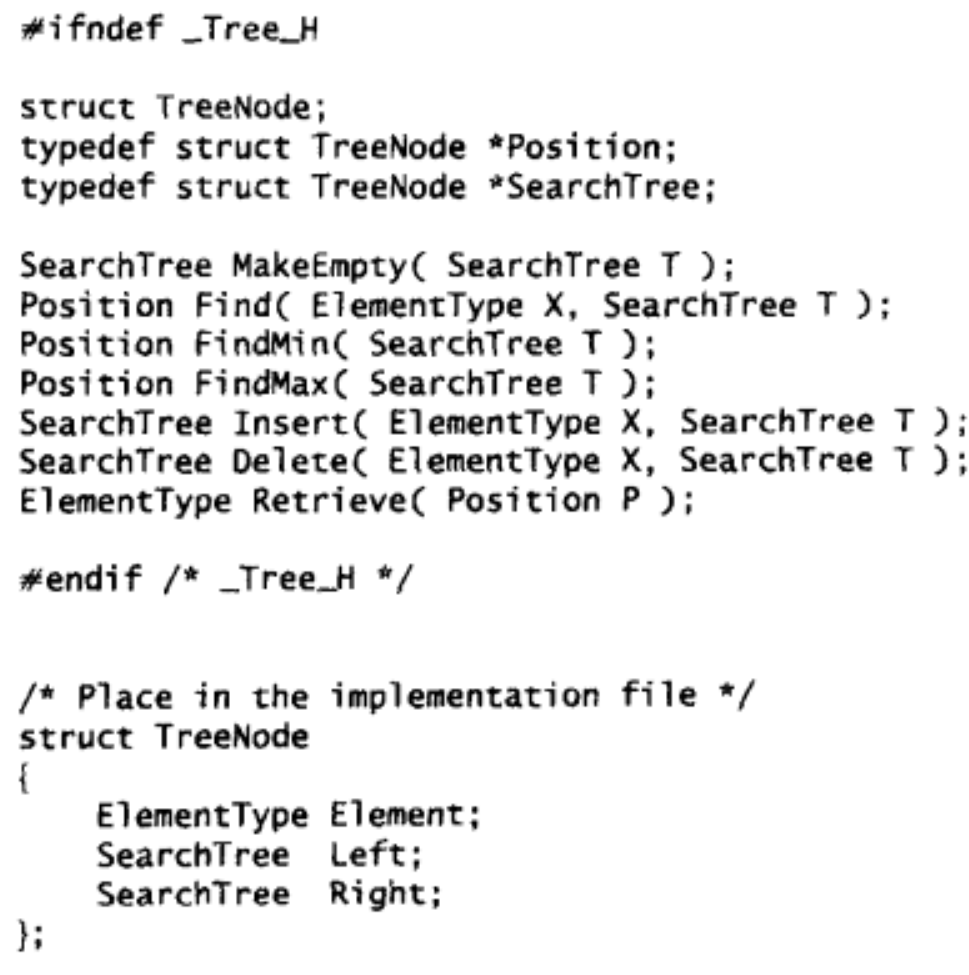
初始化MakeEmpty
将一棵树(已经存在的)初始化为一棵空树,即递归从下往上逐次释放结点的空间。
注意:在完成某结点的递归后,会回到他的父节点。

查找find
查找树的左结点关键字值 < 该结点的关键字值
返回具有关键字X的目标结点的地址Position
注意:需要对是否为空树进行测试,否则会在NULL上兜圈子

找到最小值和最大值
根据查找树的性质,左子树的结点的值 < 该结点的值,因此,只要有左结点,就一直查找他的child,直到左子树的child指向NULL,我们就到达了左节点的最深处,即最小值。同理最大值。
- FindMin查找最小值递归操作

- FindMax查找最大值的非递归操作

插入操作insert
想要将元素X插入到二叉查找树中,需要执行一段类似于find的操作,找到需要插入的结点位置。例如:
- 把5插入到下面这棵树里
首先遍历,找到5应该在的位置,不出所料,找到的时候,该位置是NULL,因此在此地malloc一个新的结点,对该节点进行赋值X,再将其左结点和右结点均赋值为NULL。
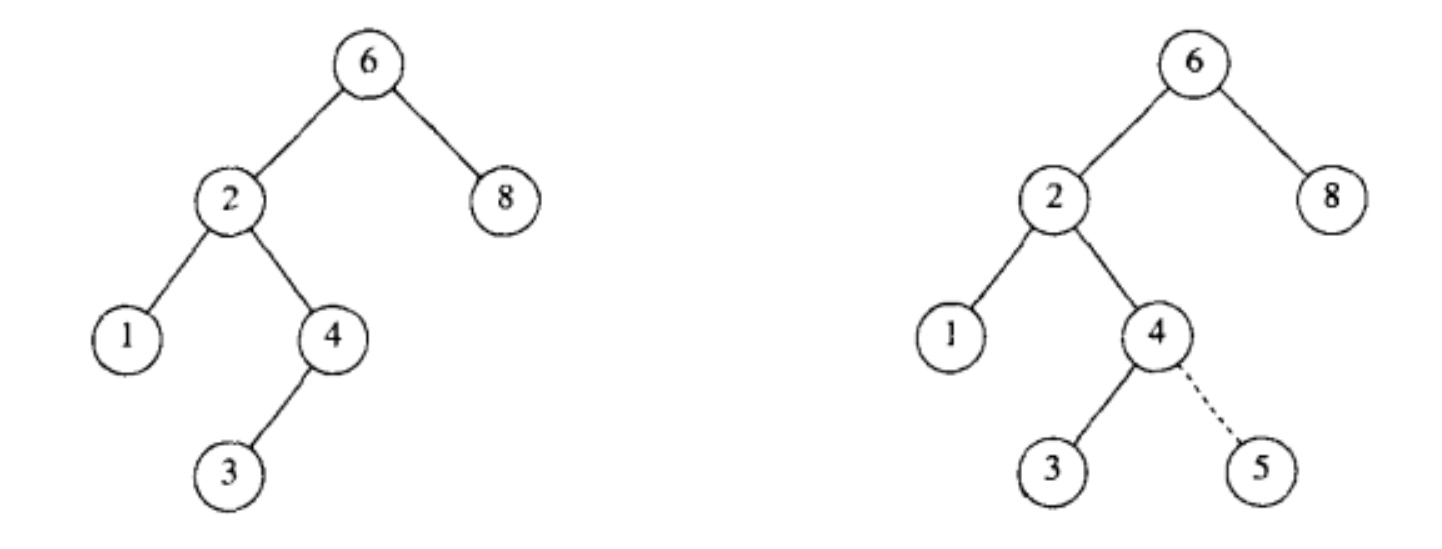
代码实现:

删除delete
- 当需要删除的结点数较少时,可以使用“懒惰删除法”,即标记需要删除的结点,不用真正的删除它。
- 当需要删除的结点数太多时,需要下面操作:
删除操作相对其他操作更复杂,一共有三种情况:
- 需要删除的结点是树叶
- 需要删除的结点有一个child
- 需要删除的结点有两个child
(1) 当情况为1时,最容易,先让该结点的父节点指向它的指针赋为NULL,然后直接free掉该树叶结点即可。
(2) 当情况为2时,例如,要删除下列树中值为4的结点,需要让其父结点指向它的child,然后free(4)。
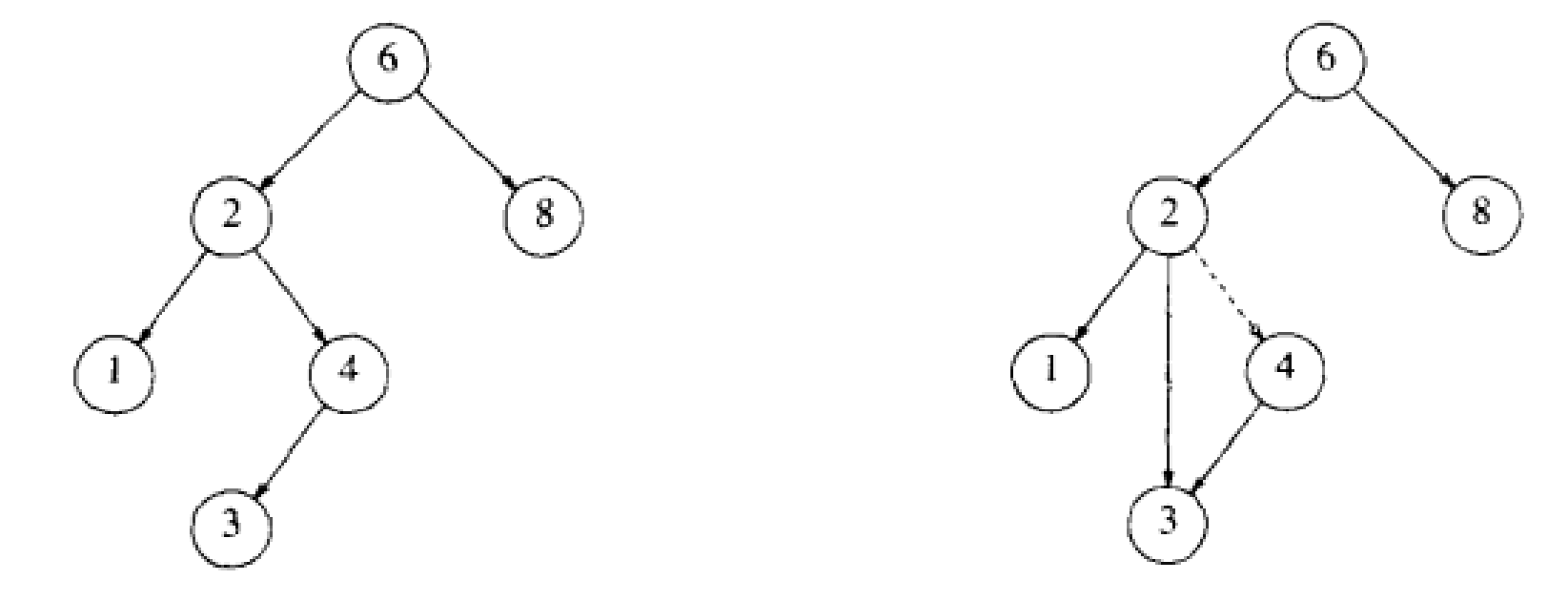
然而,当需要删除的结点没有父结点,即需要删除根结点的时候,在2情况下,需要删除的结点只有一个child,于是完全可以直接让根结点的child作为新的根,然后free掉旧的根结点。
(3) 当情况为3时,为了保证删除过后新树仍然是一颗二叉查找树,有两种策略:
- 找到比该结点大的最小结点来覆盖该结点(即:右子树最小的结点)
- 找到比该结点小的最大结点来覆盖该结点(即:左子树最大的结点)
然后free该结点。
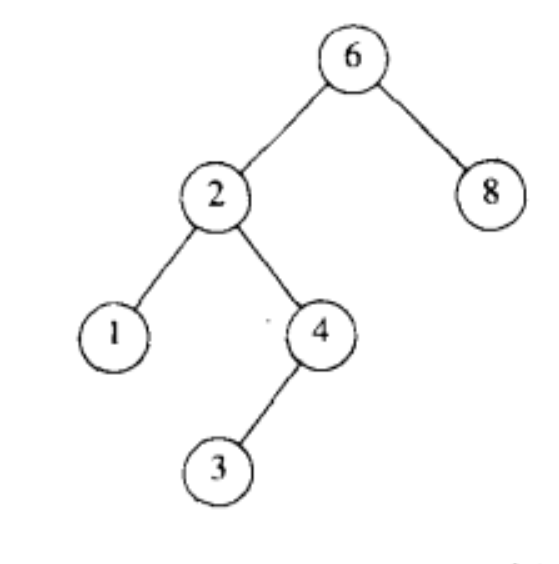
例如:需要删除下面这棵树的结点2,找到其右子树的最小结点3,让3覆盖该结点,因为3所在结点不可能有左子树(否则可以找到更小的大于2结点),所以用情况2的策略删除3结点较为容易。
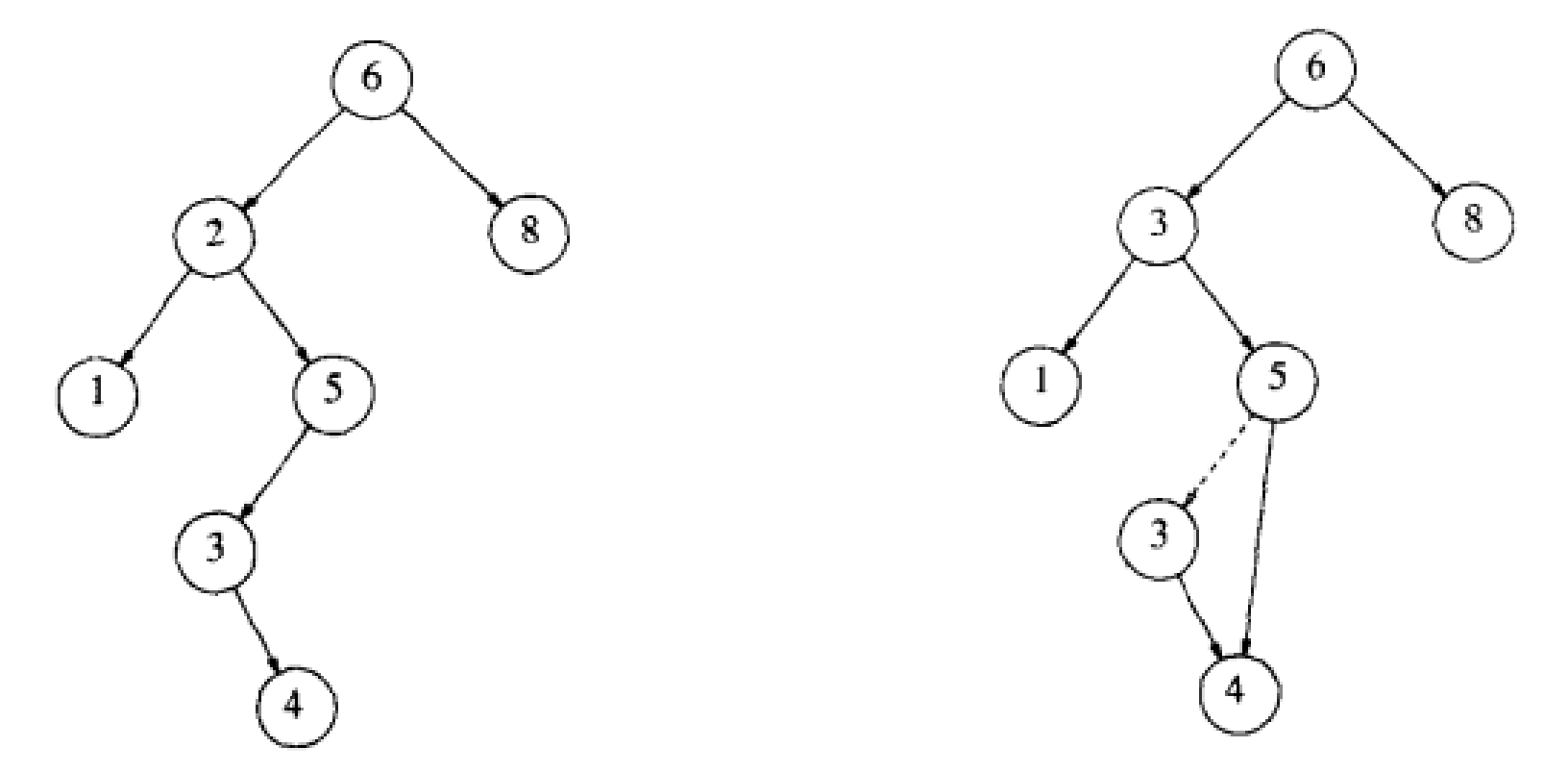
当然,我们也可以查找2结点的左子树,找到小于2的最大结点,即1,用1覆盖2结点,因为该结点不可能有右子树(否则可以找到更大的小于2的结点),所以用情况2的策略删除结点1也较为容易。
删除总操作代码实现

二叉树的平均情形分析
内部路径长:一棵树的所有结点的深度之和
上述操作的平均运行时间:O(logn)
(3)AVL平衡树
- 定义:
指任意结点左子树的高度与右子树的高度最多差1的二叉查找树——平衡。
-
优点:
优化二叉查找树,减少操作时间,提高速度。 -
任何完整二叉查找树都是AVL树。
空树高度规定为-1
- 下面的两棵树只有左边的是AVL树。
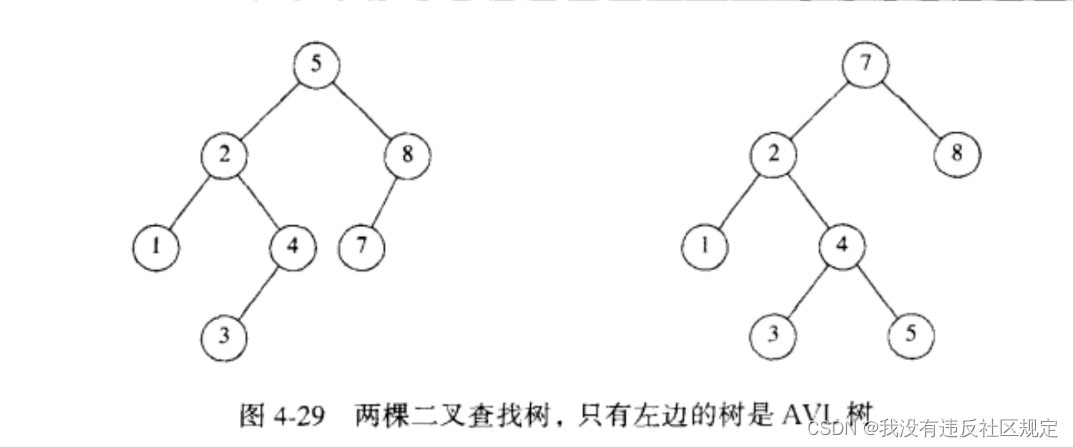
- 下面是一棵具有最少结点的高度为9的AVL tree
它的左子树是一棵具有最少结点的高度为7的AVL tree
它的右子树是一棵具有最少结点的高度为8的AVL tree
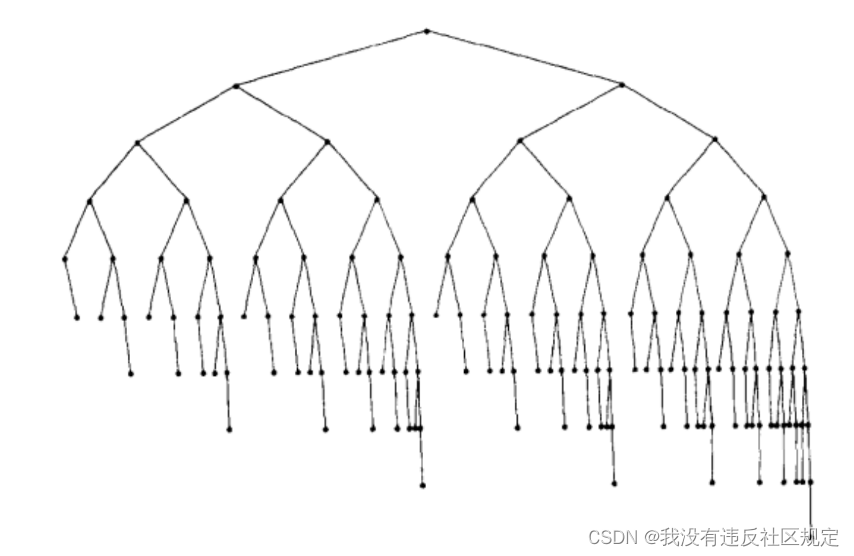
- 对于AVL 树,除了插入外,所有的操作(删除为懒惰删除操作)的操作时间都是O(logn),对于插入操作,因为插入的时候可能会破坏AVL树的平衡,因此需要做一些“调整”、“修正”rebalance,来重新平衡这棵树,使这棵树满足AVL 条件,我们称之为——“旋转”
旋转

1、2情况镜像对称,3、4情况镜像对称,然鹅在编程里看来还是四种情形。
- 对于插入在外边(1、4)的情况,使用单旋转(single rotation)
- 对于插入在内部(2、3)的情况,使用双旋转(double rotation)
判断是否需要rebalance:检查从插入结点到根节点的路径上的所有结点,看它是否平衡。直到找到需要重新平衡的结点a,或者没有找到任何一个需要平衡的结点。
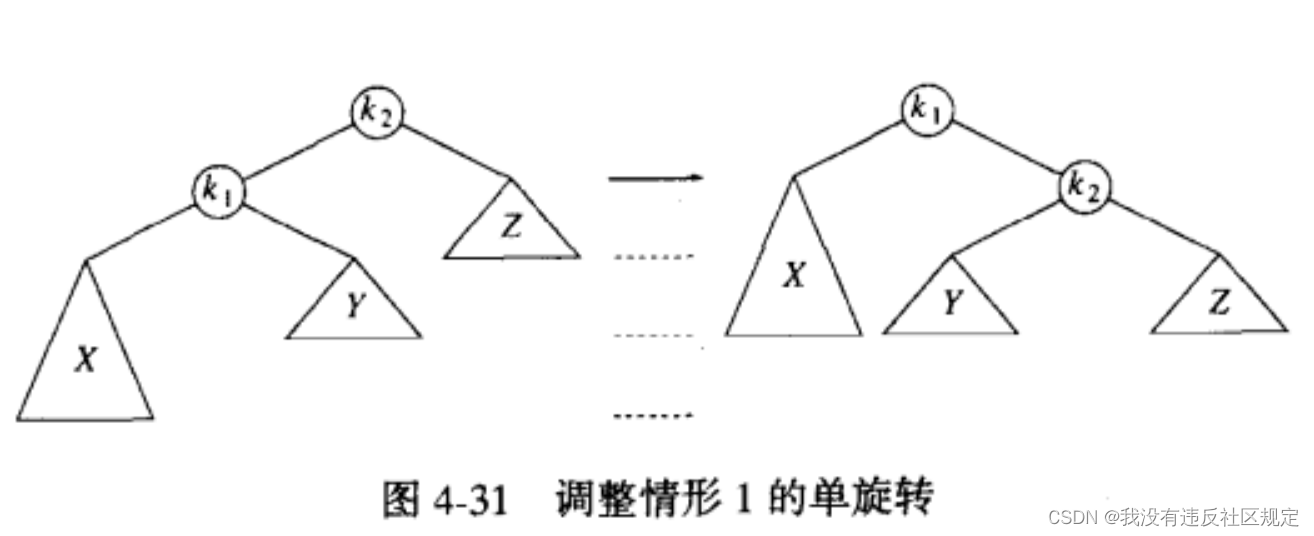
(1)单旋转single rotation
当k1结点的左子树下方插入一个元素,k2结点失去平衡(k1还是平衡的!),因此需要对k2结点进行rebalancing:
我们需要将X上移一层,Z下移一层,
因为k2结点的值 > k1结点的值,因此在调整之后将k2放在k1的右子树,依然还是一棵AVL树。
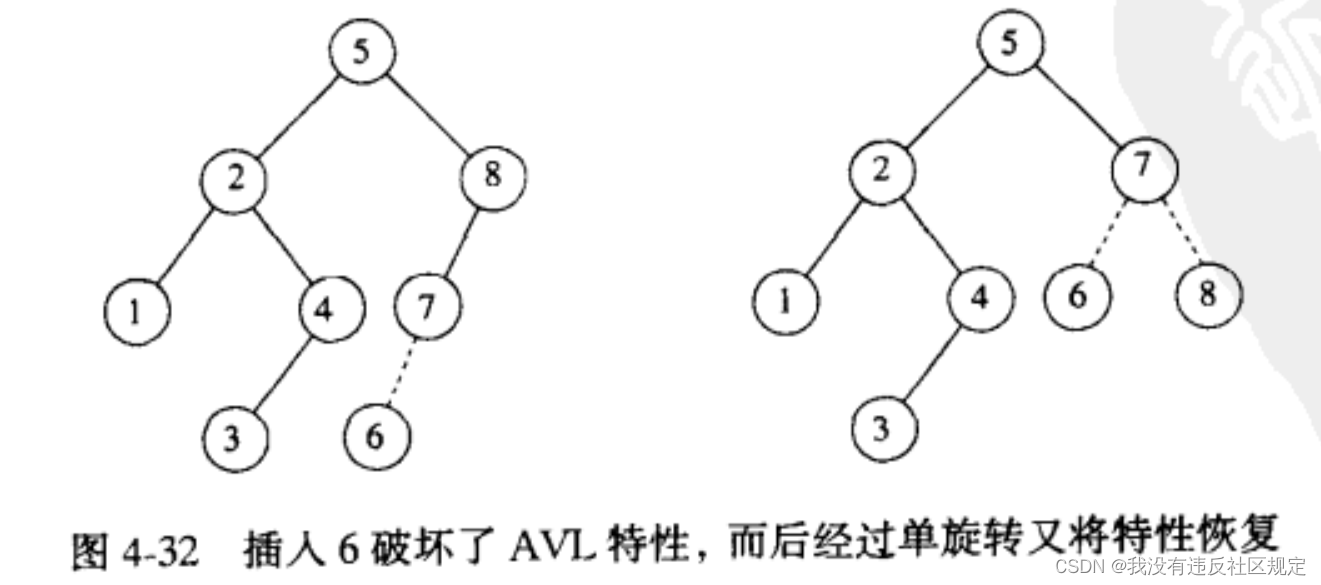
举例
插入6破坏了AVL的特性,结点8不再平衡,因此需要对结点7、8进行一次单旋转。
(2)双旋转 double rotation
当插入子树的深度太深,即情况2、3时,所插入的结点是不平衡结点的右子树的左儿子,或左子树的右儿子,单旋转不能解决问题,此时需要用到双旋转。
如下图,k3、k1都不能再作为根节点,此时只能让k2作为根节点,k1成为它的左儿子,k3成为它的右儿子,B、C分别作为左子树的右儿子和右子树的左儿子。
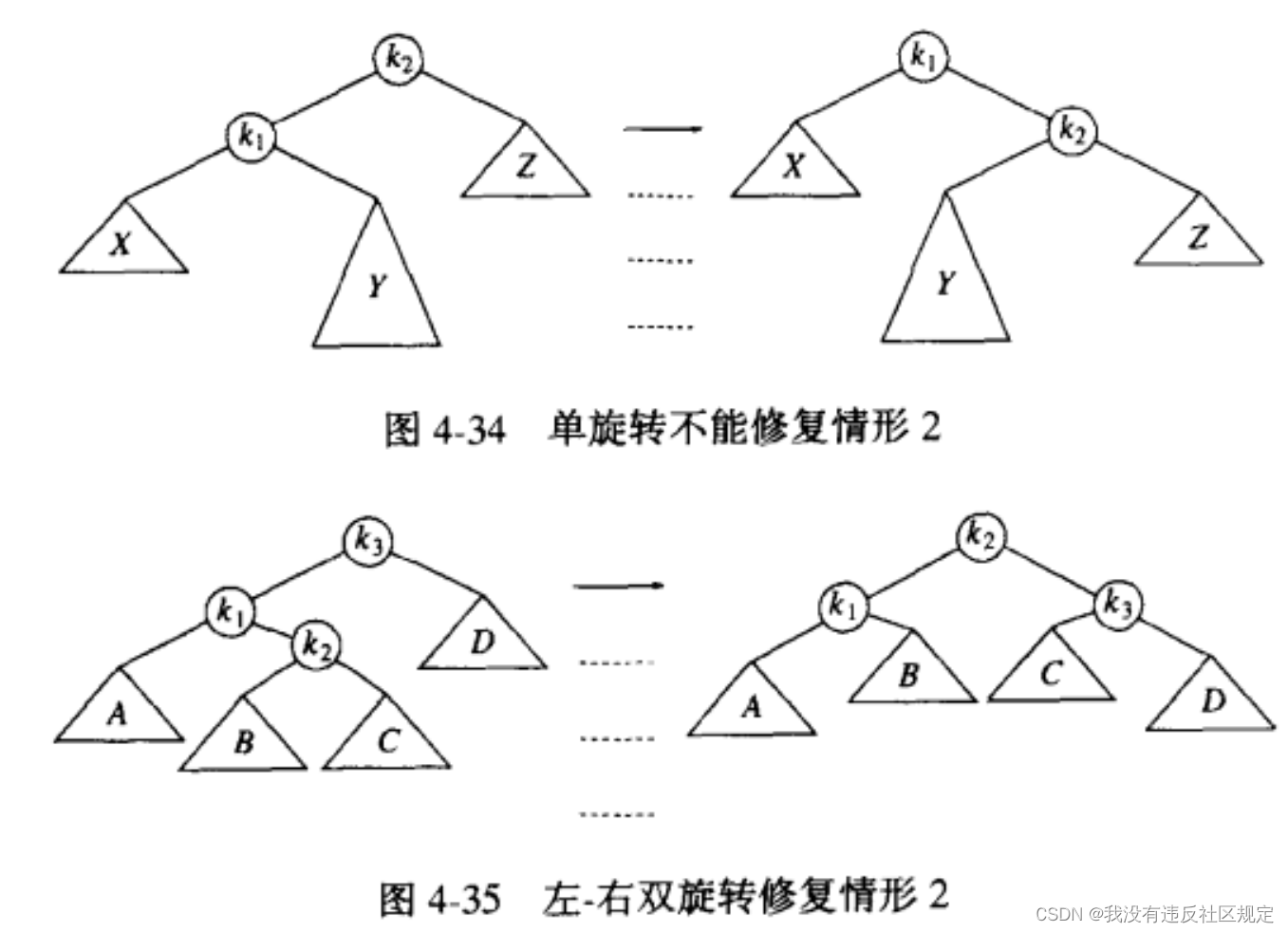
例如在下面这棵AVL树,插入关键字为14的结点,导致结点6失去平衡,经过观察,所插入结点的位置是失去平衡结点(6结点)的右子树的左子树里,因此需要采取双旋转。
让所插入结点的父结点(7结点)替代6结点所在位置,6结点作为7结点的左儿子,15结点作为7结点的右儿子。
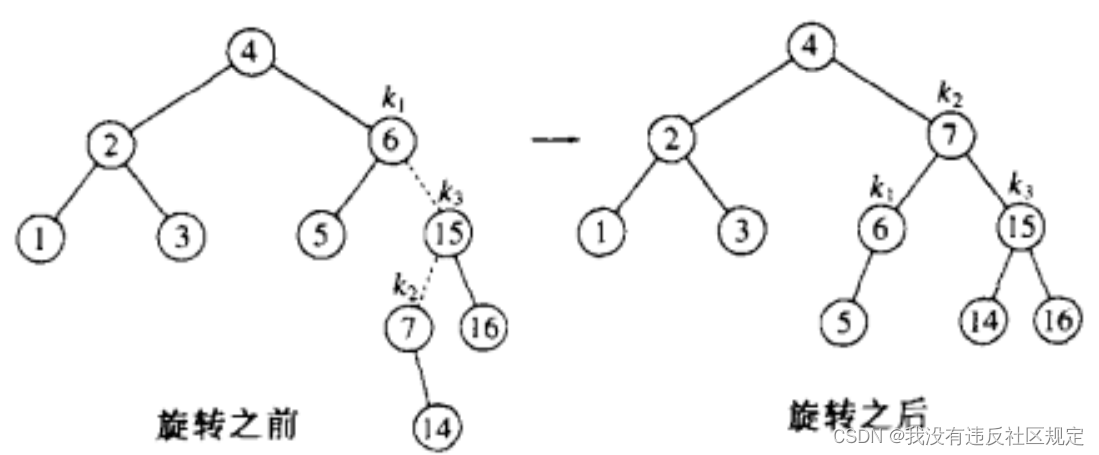
总结

相关代码及解释
(1)声明
struct AvlNode;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;
struct AvlNode {
ElementType Element;
AvlTree Left;
AvlTree Right;
int Height;
};
(2)获得某结点的高度
下面复杂度为O(1)
int height(Position P) {
return (P == NULL) ? -1 : P->Height;
}
下面复杂度为O(n)
int height(Position P) {
if (P->Left == NULL)
return (P->Right == NULL) ? 0 : 1 + height(P->Right);
else
return (P->Right == NULL) ?
1 + height(P->Left) : 1 + height(P->Left) – height(P->Right);
}
(3)插入结点

(4)执行单旋转

(5)执行双旋转























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








