查找算法总结

静态查找结构主要有两种：顺序查找、折半查找

 

一、顺序查找：这个就不用说了，一个一个的差吧，很差劲的算法了，时间复杂度是O(n)

      public  int shunXuSearch(  int[] b,  int c) {

            for (  int i = 0; i < b. length; i++) {

                if (b[i] == c) {

                   System.  out.println( "查到了您想要的结果" + c + "，位置在：" + i);

                     return i;

              }

          }

          System.  out.println( "sorry！没有查询到您想要的结果！" );

            return -1;

     }

二、折半查找、二分查找：这个需要查找对象是有序的，每一次都找1/2的部分，查找次数大大的减少了。时间复杂度是O(logN)。

   折半查找其实就是一颗二叉树的遍历，其中，中间的元素就是二叉树的根。这里有个问题，如果这个根一年半载才查找一次，而这棵树的叶子需要1秒钟就查找一次，那么这种折半查找是否还有效率呢？就很坑了吧。所以才有了后面的集中查找算法。另外，如果想要添加、或者删除一个数据的时候，整个结构都需要重建，这个代价是不可估量的。

   折半查找方法适用于不经常变动而查找频繁的有序列表

      public  int binarySearch(  int[] b,  int c) {

           // 这里需要先排序，假设已经是有序的数组了

            int low = 0;

            int high = b. length - 1;

            int middle;

            while (low <= high) {

              middle = (high + low) / 2;

                if (c == b[middle]) {

                   System.  out.println( "您要找的结果" + c + "已经找到，位置在：" + middle);

                     return middle;

              }  else  if (c > b[middle]) {

                   low = middle + 1;

              }  else  if (c < b[middle]) {

                   high = middle - 1;

              }

          }

          System.  out.println( "sorry！这里没有您想要的结果！" );

            return -1;

     }

 

接下来的几种算法属于动态查找结构

三、二叉查找树：

     特点：

     1、如果它的左子树不空，那么左子树上的所有结点值均小于它的根结点值；

     2、如果它的右子树不空，那么右子树上的所有结点值均大于它的根结点值；

     3、它的左右子树也分别为二叉查找树。

 

二叉查找树的插入和删除都非常的方便，很好的解决了折半查找添加删除所带来的问题。

那么它的效率又如何呢？

很显然，二叉查找树查找一个数据，不需要遍历全部的节点，查找效率确实提高了。但是，也有一个很严重的问题，我在a图中查找8需要比较5次，而在b图中查找8需要3次，更为严重的是，我的二叉查找树是c图，如果再查找8，那将会如何呢？很显然，整棵树就退化成了一个线性结构，此时再查找8，就和顺序查找没什么区别了。

时间复杂度分析：最坏的情况下和顺序查找相同，是O(N)，最好的情况下和折半查找相同，是O(logN)。

 

这说明了一个问题，同样的一组数据集合，不同的添加顺序会导致二叉查找树的结构完全不一样，直接影响到了查找的效率。

那么如何解决这个问题呢？

往后看，还有别的算法呢。二叉查找树的代码分析可以参考另一篇文章《二叉查找树算法专题》

 

四、平衡二叉树

     上面说了，二叉树在某种情况下会存在效率问题，不同结构的二叉查找树，查找的效率会有很大的不同，那么怎么解决这个问题呢？那就需要最大限度的减小树的深度。

     平衡二叉树的一个很大的优点就是不会出现二叉查找树的最差情况。

     平衡二叉树的时间复杂度是O(logN)。

     接下来看看平衡二叉树的查找、插入，以及删除等操作是如何实现的。

     查找就不多说了，与二叉查找树基本相同；

     那么插入如何呢？ 首先第一步是先插入进去，然后，为了保持二叉树的平衡，就需要左旋或者右旋等操作了。

     删除也是同样的道理。 一会儿我们可以通过代码分析左旋右选的实现了，不过你如果想了解左旋右旋的基本概念，那还是在网上查看一下这方面的知识吧。

 

     知道了优点，那么我们再来分析一下平衡二叉树又有哪些缺陷呢？

     

主要有这么几个缺陷：

1、为了保证高度平衡，动态插入和删除的代价也随之增加，我们可以通过红黑树来实现更高效率的查找结构；

2、所有二叉查找树结构的查找代价都与树高有紧密的联系，能否通过减少树高来进一步的降低查找代价呢？

我们可以通过多路查找树的结构来做到这一点；

3、在大数据量查找环境下，所有的二叉查找树结构（BST,AVL,RBT)都不合适，如此大规模的数据，全部组织成平衡二叉树放入到内存中是不可能的。那么把这棵树放到磁盘中吧，问题又来了。假如构造的平衡二叉树深度有1W层，那么从根节点出发到叶子节点很可能需要1W次的硬盘I/O读写。查找效率在IO读写过程中将会付出巨大的代价。

 

那个提个问题：

N层平衡二叉树至少多少个结点？

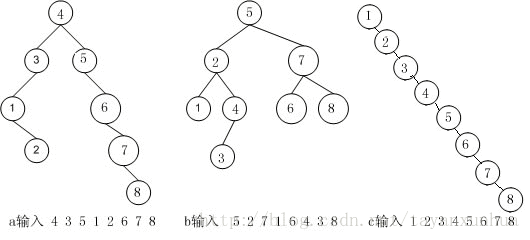
假设F(N)表示N层平衡二叉树的结点个数，则F[1]=1，F[2]=2。而F(N)=F(N-2)+F(N-1)+1 

为什么呢？我们可以这样考虑，假设现在又一个(N-2)层和(N-1)层的最少结点平衡二叉树。要构造一棵N层的平衡二叉树，则只需加入一个根节点，其左右子树分别(N-2)层和(N-1)层的树即可 。由于两个子树都是最少结点的，所有N层的也是最少结点的。

以前我一直没理解这个问题，后来我画了一个图，立马分析透彻了。

平衡二叉树的代码就不写了，真心难搞啊，网上有很多的资料。

 

五、红黑树

性质：

     1、每一个节点要么是红色的，要么是黑色的；

     2、根节点是黑色的；

     3、所有叶子节点都是黑色的（实际上都是NULL指针），叶子节点不包含任何关键字信息，所有的关键字信息都存在非终结点上面；

     4、每个红色节点的两个子节点都是黑色的，换句话说：从每个叶子节点到根节点的所有路径不能有两个连续的红色的节点；

     5、从任一节点到每个叶子节点的所有路径都包含相同数目的黑色节点。

 

相关定理：

     1、从根到叶子节点的最长的可能路径长度不多于最短的可能路径长度的2倍；

     2、红黑树的树高不大于2倍的红黑树的黑深度；

     3、一颗拥有n个内部节点(红黑树的非终结点)的红黑树的树高h<=2log(n+1)。

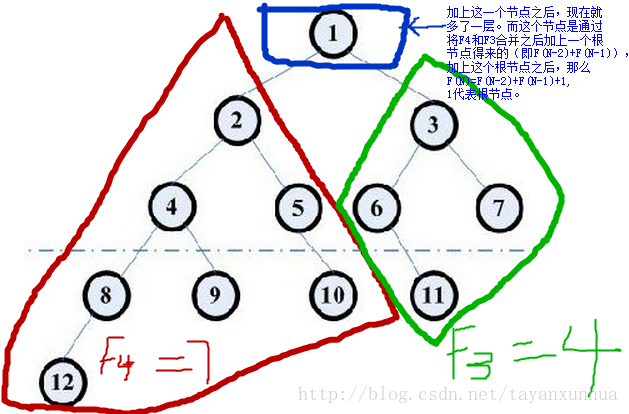
在对红黑树插入的时候，我们一般都会插入红色的结点，红黑树的插入主要有这几种情况：

1、插入的是根结点；

     此时，只会违反性质2，那么直接把此结点涂为黑色即可。

2、插入的结点的父节点是黑色的；

     此时什么都不需要做。

3、插入的结点的父节点是红色且叔父结点是红色；

     此时又分为几种情况：

          1）、父节点是祖父结点的左子树还是右子树；     

          2）、插入的结点是父节点的左子树还是右子树。

     无论哪种情况，解决策略都是：

          对插入的结点（当前结点）的父节点和叔父结点涂黑，祖父结点涂红，把当前结点指向祖父结点，递归执行第1种情况。

4、插入的结点的父节点是红色，叔父结点是黑色的。

     这种情况又分为以下几种情况：

     1）、插入结点为父结点的左结点，父节点为祖父结点的左结点；

          解决方案：父节点变黑，祖父结点变红，然后以祖父结点为支点右旋。

     2）、插入结点为父节点的右节点，父节点为祖父结点的左结点；

          解决方案：以当前结点的父节点为支点左旋，然后再以当前结点的左结点执行第1）种情况。

     3）、插入结点为父节点的左结点，父节点为祖父结点的右节点；

          解决方案：以当前结点的父节点为支点右旋，然后再以当前结点的右节点执行第4）中情况。

     4）、插入结点为父节点的右节点，父节点为祖父结点的右节点。

          解决方案：父节点变黑，祖父结点变红，然后以祖父结点为支点左旋。

 

代码实现如下：

[java]  view plain  copy

 

 

1. package com.tyxh.rab;  
2.   
3. public class TreeNode {  
4.      public int data;  
5.      public TreeNode lchild;  
6.      public TreeNode rchild;  
7.      public TreeNode parent;  
8.      public boolean color;  
9.      public TreeNode( int data, TreeNode lchild, TreeNode rchild,  
10.               TreeNode parent, boolean color) {  
11.            this. data = data;  
12.            this. lchild = lchild;  
13.            this. rchild = rchild;  
14.            this. parent = parent;  
15.            this. color = color;  
16.      }  
17.        
18. }  

[java]  view plain  copy

 

 

1. package com.tyxh.rab;  
2.   
3. public class BTTree {  
4.      public static final boolean RED = false;  
5.      public static final boolean BLACK = true;  
6.      private TreeNode root;  
7.   
8.      public BTTree() {  
9.            root = null;  
10.      }  
11.   
12.      public TreeNode grandParentNode(TreeNode node) {  
13.            // 获得祖父节点  
14.            return node. parent. parent;  
15.      }  
16.   
17.      public TreeNode uncleParentNode(TreeNode node) {  
18.            // 获得叔父节点  
19.            if (node. parent == grandParentNode(node). lchild)  
20.                return grandParentNode(node). rchild;  
21.            else  
22.                return grandParentNode(node). lchild;  
23.      }  
24.   
25.      // 左旋  
26.      private void singRotateLeft(TreeNode k2) {  
27.           TreeNode k1 = k2. rchild;  
28.           k2. rchild = k1. lchild;  
29.           k1. lchild = k2;  
30.      }  
31.   
32.      // 右旋  
33.      private void singRotateRight(TreeNode k2) {  
34.           TreeNode k1 = k2. lchild;  
35.           k2. lchild = k1. rchild;  
36.           k1. rchild = k2;  
37.      }  
38.   
39.      // 插入  
40.      // 1、新结点位于树的根上，没有父节点  
41.      public void insert_case1(TreeNode node) {  
42.            if (node. parent == null)  
43.               node. color = BLACK;  
44.            else  
45.               insert_case2(node);  
46.      }  
47.   
48.      // 2、新节点的父节点是黑色的  
49.      public void insert_case2(TreeNode node) {  
50.            if (node. parent. color == BLACK)  
51.                return;  
52.            else  
53.               insert_case3(node);  
54.      }  
55.   
56.      // 3、父节点是红色的，叔父节点也是红色的  
57.      public void insert_case3(TreeNode node) {  
58.            if (uncleParentNode(node) != null && uncleParentNode(node).color == RED ) {  
59.               node. parent. color = BLACK;  
60.               uncleParentNode(node). color = BLACK;  
61.               grandParentNode(node). color = RED;  
62.               insert_case1(grandParentNode(node));  
63.           } else  
64.               insert_case4(node);  
65.      }  
66.   
67.      // 4、父节点是红色的，叔父结点是黑色的或者为Nil，并且插入结点是父节点的右节点，父节点是祖父结点的左结点  
68.      public void insert_case4(TreeNode node) {  
69.            if (node == node. parent. rchild  
70.                    && node. parent == grandParentNode(node).lchild) {  
71.                // 以node.parent为结点左旋  
72.               singRotateLeft(node. parent);  
73.               node = node. lchild;  
74.           } else if (node == node. parent. lchild  
75.                    && node. parent == grandParentNode(node).rchild) {  
76.                // 以node.parent为结点右旋  
77.               singRotateRight(node. parent);  
78.               node = node. rchild;  
79.           }  
80.           insert_case5(node);  
81.      }  
82.   
83.      // 5、父亲结点是红色的，叔父是黑色的或者为Nil，并且插入结点是父节点的左结点，父节点是祖父结点的左结点  
84.      public void insert_case5(TreeNode node) {  
85.           node. parent. color = BLACK;  
86.           grandParentNode(node). color = RED;  
87.            if (node == node. parent. lchild  
88.                    && node. parent == grandParentNode(node).lchild) {  
89.                // 以祖父结点为结点右旋  
90.               singRotateRight(grandParentNode(node));  
91.           } else if (node == node. parent. rchild  
92.                    && node. parent == grandParentNode(node).rchild) {  
93.                // 以祖父结点为结点左旋  
94.               singRotateLeft(grandParentNode(node));  
95.           }  
96.   
97.      }  
98.   
99.      // 中序遍历  
100.      public void traversal() {  
101.           insubtree( root);  
102.      }  
103.   
104.      private void insubtree(TreeNode node) {  
105.            if (node == null)  
106.                return;  
107.           insubtree(node. lchild);  
108.           System. out.println(node. data + "、");  
109.           insubtree(node. rchild);  
110.      }  
111. }  

 

 

六、多路查找树、B~树、B+树

      B树一种多路查找树（维基百科中定义）：存储排序数据并允许以O(log n)的运行时间进行查找，顺序读取，插入和删除的数据结构。B树，概括来说是一个节点可以拥有多于2个子节点的二叉查找树。也可以说是 B- 或 B~树。

     术语Ｂ树可以指一个特定的方案，也可以指大体上一类方案。狭义上，一个Ｂ树在它内部节点中存储键值，但不需在叶子节点上存储这些键值的记录。大体上的一类包含一些变体，如B+树或B*树。

 

【B~ 树】

      B- 树，又叫做平衡多路查找树，一颗 m 阶的B- 树 （也可以说是m叉树） 的特征如下：
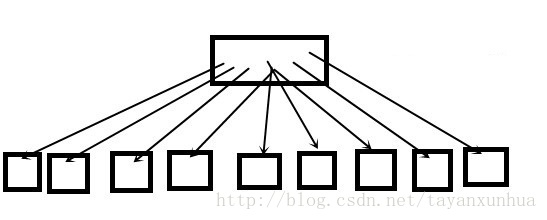
1、树中每个结点最多有 m 个孩子；
2、除根结点和叶子节点外，其他每个节点至少有 m / 2 个孩子；
3、若根结点不是叶子节点，则至少有 2 个孩子；
4、所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息
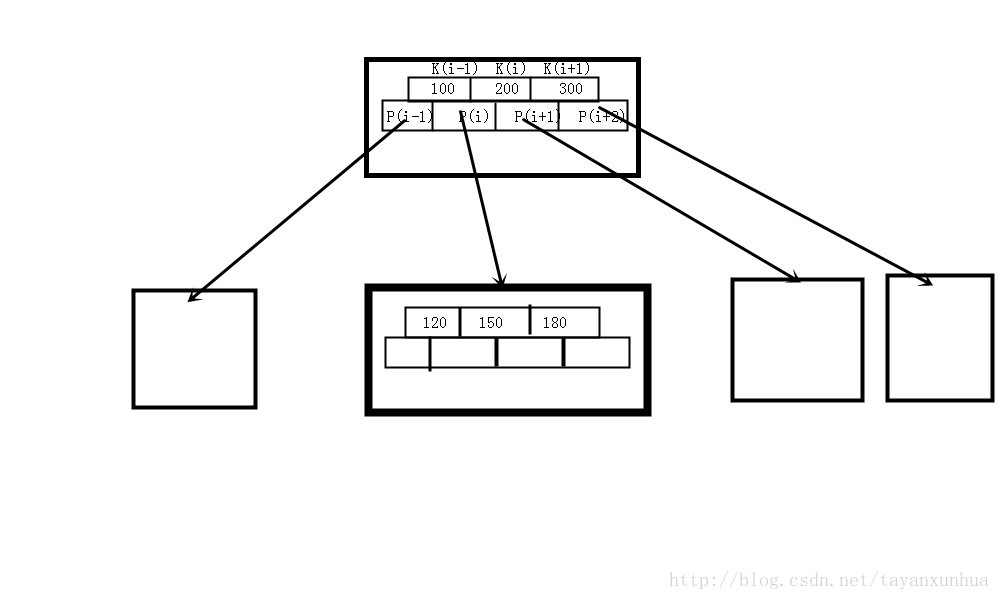
5、每个非终结点中包含 n 个关键字信息：（n, P0, K1, P1, K2, P2, ... , Kn, Pn）。其中，
     a、Ki(i=1...n)为关键字，且关键字按顺序排序Ki < K(i-1)
     b、Pi为指向子树的结点，且指针P(i-1)指向子树中所有结点的关键字均小于Ki，但是大于K(i-1)
     c、关键字的个数 n 必须满足：m/2 - 1 <= n <= m-1

6、有n棵子树的结点中含有 n-1 个关键字(即K所表示i的内容)

 

     关于b所述的内容，一直没有理解明白，后来还是通过这张图才理解，此图中我省略了一些节点，仅仅画出了Pi指向的那个节点，这个节点中的关键字全部都是大于K(i-1)，并且小于Ki 的。（注意：P 的个数 比 K 的个数多 1 个）

 

 

举例分析：下面就是一棵3阶B~树

（为了简单，这里用少量数据构造一棵2-4树的形式，其实实际应用中的B树结点中关键字很多的）

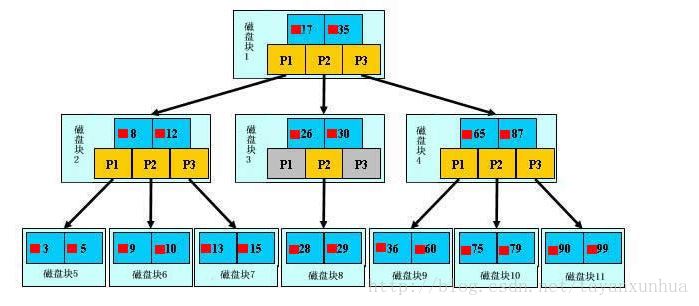
现在我们模拟查找文件29的过程：

      (1) 根据根结点指针找到文件目录的根磁盘块1，将其中的信息导入内存。【磁盘IO操作1次】

      (2) 此时内存中有两个文件名17，35和三个存储其他磁盘页面地址的数据。根据算法我们发现17<29<35，因此我们找到指针p2。

      (3) 根据p2指针，我们定位到磁盘块3，并将其中的信息导入内存。【磁盘IO操作2次】

      (4) 此时内存中有两个文件名26，30和三个存储其他磁盘页面地址的数据。根据算法我们发现26<29<30，因此我们找到指针p2。

      (5) 根据p2指针，我们定位到磁盘块8，并将其中的信息导入内存。【磁盘IO操作3次】

     (6) 此时内存中有两个文件名28，29。根据算法我们查找到文件29，并定位了该文件内存的磁盘地址。

 

分析一下上面的过程，

     我们发现需要3次磁盘IO操作和3次内存查找操作。关于内存中的文件名查找，由于是一个有序表结构，可以利用折半查找提高效率。至于3次磁盘IO操作时影响整个B~树查找效率的决定因素。

      当然，如果我们使用平衡二叉树的磁盘存储结构来进行查找，磁盘IO操作最少4次，最多5次。而且文件越多，B~树比平衡二叉树所用的磁盘IO操作次数将越少，效率也越高。

 

【B+树】

B+ 树 是应文件系统所需而产生的中B~树的变形树。B+ 树元素自底向上插入，这与二叉树恰好相反。

 

一颗 m 阶的B+树和 m 阶的B-树的异同在于：

     1、有n棵子树的结点中含有 n - 1个关键字； (与B 树n棵子树有n-1个关键字相同)

     2、所有叶子节点包含了全部的关键字信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小从小到大的顺序链接。（而B树的叶子结点并没有包含全部需要查找的信息）

     3、所有非终结点都可以看出是索引部分，结点中仅含有其子树根结点中最大或最下关键字。（B树的非终结点也包含需要查找的有效信息）

 

      B+树的内部结点并没有指向关键字具体信息的指针（而B树则会包括，因为B树内部结点包含关键字信息），这样就会导致B+树的内部结点相对于B树来说小一些。如果把同一个内部结点的关键字存放在同一个盘块儿中， 那么盘块儿所能容纳的关键字数量也就越多，那么一次性读入内存中的需要查找的关键字也就越多，相对来说IO读写次数就会减少。

     举个例子吧：

     假设磁盘中一个盘块儿容纳16bytes，而一个关键字是2bytes，一个关键字具体信息指针是2bytes。

     一棵9阶B~树(一个结点最多8个关键字)的内部结点需要2个盘快。而B+树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B~树就比B+数多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

     如果没有明白，再详细的分析一下：假设树是这样的。

 

 假设这个是 9阶 B树或B+树的某个节点，那么这个节点至少有 9/2 个孩子， 最多有9个孩子。

 

     如果是B树的情况下：

     当有9个孩子的时候，则有8个关键字（n-1的关系），同时也具有8个关键字具体信息的指针（这些指针用来指向这个关键字在这个内部结点存储的位置，例如上面B树中的小红色块儿区域），如果我们只保存这个内部结点的信息，需要的存储空间是 9*2 + 8*2 + 8*2 = 50(bytes)； 当有4个孩子的时候，则有3个关键字，同时也具有3个关键字具体信息的指针，内部结点需要的存储空间是 4*2 + 3*2 + 3*2 = 20(bytes)。所以这个内部节点最少需要20bytes（即2个盘块儿），最多需要50bytes（即4个盘块儿）。

 

 

     如果是B+树的情况下：

     当有9个孩子的时候，则有8个关键字，但是没有8个关键字的具体信息指针，那么内部结点需要的内存空间是 9*2 + 8*2 = 34(bytes)；当有4个孩子的时候，则有3个关键字，但是没有3个关键字的具体信息指针，那么内部结点需要的内存空间是4*2 + 3*2 = 14(bytes)。所以这个内部结点最少需要14bytes(即1个盘块儿)，最多需要34bytes(即3个盘块儿)。

     

     从上面的分析中就可以看出，无论怎样，在相同的条件下，即无论是B树还是B+树，在这个内部节点有相同的孩子树的时候，读取这个内部节点信息的时候，B树进行的IO操作会多一些。

     

为什么说B+-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引？

     第一点就是刚刚我们再上面所讲到的内容：即B+树的磁盘读写代价更低；

     第二点就是B+树的查询效率更加稳定。

          第二点怎么解释呢？由于非终结点并不是最终指向文件内容的结点（即没有存储关键字的 具体信息），而只是存储叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根节点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率都相当。

 

B+树相对于B树的优点：

     1、B+树非常容易扫库，即很容易查询出所有的数据，直接从叶子结点挨个扫一遍句完事儿了，但是B树必须用中序遍历的方法进行遍历；

     2、B+树支持range-query非常方便，而B树不支持。这是数据库选用B+树的最主要原因。

     比如要查 5-10之间的，B+树一把到5这个标记，再一把到10，然后串起来就行了，B树就非常麻烦。B树的好处，就是成功查询特别有利，因为树的高度总体要比B+树矮。不成功的情况下，B树也比B+树稍稍占一点点便宜。
    B树比如你的例子中查，17的话，一把就得到结果了，有很多基于频率的搜索是选用B树，越频繁query的结点越往根上走，前提是需要对query做统计，而且要对key做一些变化。     

   另外B树也好B+树也好，根或者上面几层的节点因为被反复query，所以这几块基本都在内存中，不会出现读磁盘IO，一般在启动的时候，就会主动放入内存。 

 

 

【B* 树】

B*-tree是B+-tree的变体，在B+树的基础上(所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针)，B*树中非根和非叶子结点再增加指向兄弟的指针；B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。给出了一个简单实例，如下图所示：

 

      B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。
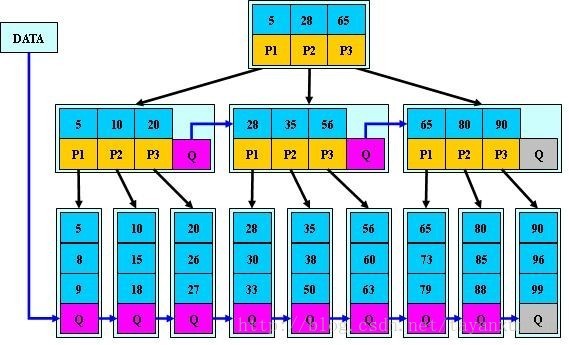
      B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。
     所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

 

几种查找算法分析就分析到这里，我也是根据几篇文章进行总结的，其中大部分的内容来自于 爪哇人的博客和 结构算法 算法之道的博客，对于一些比较难懂的内容，又添加了自己的分析，如有问题，可以留下评论一起讨论。

 

补充：

基本概念

结点的层次（Level）从根开始定义，根为第一层，根的孩子为第二层。

二叉树的高度：树中结点的最大层次称为树的深度（Depth）或高度。

 

二叉树

在计算机科学中，二叉树是每个结点最多有两个子树的有序树。通常子树的根被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用作二叉查找树和二叉堆。二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2的（i-1）次方个结点；深度为k的二叉树至多有2的k次 − 1个结点；对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0 = n2 + 1。

树和二叉树的2个主要差别：

1. 树中结点的最大度数没有限制，而二叉树结点的最大度数为2；

2. 树的结点无左、右之分，而二叉树的结点有左、右之分。……

树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很象自然界中的树那样。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到广泛应用，如在编译源程序如下时，可用树表示源源程序如下的语法结构。又如在数据库系统中，树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可用树来描述。

一、树的概述

树结构的特点是：它的每一个结点都可以有不止一个直接后继，除根结点外的所有结点都有且只有一个直接前趋。以下具体地给出树的定义及树的数据结构表示。

（一）树的定义

树是由一个或多个结点组成的有限集合，其中：

⒈必有一个特定的称为根(ROOT)的结点；

⒉剩下的结点被分成ｎ>=0个互不相交的集合T1、T2、......Tn，而且， 这些集合的每一个又都是树。树T1、T2、......Tn被称作根的子树(Subtree)。

树的递归定义如下：（1）至少有一个结点（称为根）（2）其它是互不相交的子树

1.树的度——也即是宽度，简单地说，就是结点的分支数。以组成该树各结点中最大的度作为该树的度，如上图的树，其度为3;树中度为零的结点称为叶结点或终端结点。树中度不为零的结点称为分枝结点或非终端结点。除根结点外的分枝结点统称为内部结点。

2.树的深度——组成该树各结点的最大层次，如上图，其深度为4；

3.森林——指若干棵互不相交的树的集合，如上图，去掉根结点A，其原来的二棵子树T1、T2、T3的集合{T1,T2,T3}就为森林；

4.有序树——指树中同层结点从左到右有次序排列，它们之间的次序不能互换，这样的树称为有序树，否则称为无序树。

5.树的表示

树的表示方法有许多，常用的方法是用括号：先将根结点放入一对圆括号中，然后把它的子树由左至右的顺序放入括号中，而对子树也采用同样的方法处理；同层子树与它的根结点用圆括号括起来，同层子树之间用逗号隔开，最后用闭括号括起来。如上图可写成如下形式：

(A(B(E(K,L),F),C(G),D(H(M),I,J)))

5. 2 二叉树

1.二叉树的基本形态：

二叉树也是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态：

(1)空二叉树——(a)；

(2)只有一个根结点的二叉树——(b)；

(3)只有右子树——(c)；

(4)只有左子树——(d)；

(5)完全二叉树——(e)

注意：尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。

2.两个重要的概念：

(1)完全二叉树——只有最下面的两层结点度小于2，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树；

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶结点都处在最底层的二叉树,。

3.二叉树的性质

(1) 在二叉树中，第i层的结点总数不超过2^(i-1)；

(2) 深度为h的二叉树最多有2^h-1个结点(h>=1)，最少有h个结点；

(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，

则N0=N2+1；

(4) 具有n个结点的完全二叉树的深度为int（log2n）+1

(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：

若I为结点编号则 如果I<>1，则其父结点的编号为I/2；

如果2*I<=N，则其左儿子（即左子树的根结点）的编号为2*I；若2*I>N，则无左儿子；

如果2*I+1<=N，则其右儿子的结点编号为2*I+1；若2*I+1>N，则无右儿子。

(6)给定N个节点，能构成h(N)种不同的二叉树。

h(N)为卡特兰数的第N项。h(n)=C(n,2*n)/(n+1)。

4.二叉树的存储结构：

(1）顺序存储方式

type node=record

data:datatype

l,r:integer;

end;

var tr:array[1..n] of node;

(2)链表存储方式，如：

type btree=^node；

node=record

data:datatye;

lchild,rchild:btree;

end;

5.普通树转换成二叉树：凡是兄弟就用线连起来，然后去掉父亲到儿子的连线，只留下父母到其第一个子女的连线。

二叉树很象一株倒悬着的树，从树根到大分枝、小分枝、直到叶子把数据联系起来，这种数据结构就叫做树结构，简称树。树中每个分叉点称为结点，起始结点称为树根，任意两个结点间的连接关系称为树枝，结点下面不再有分枝称为树叶。结点的前趋结点称为该结点的"双亲"，结点的后趋结点称为该结点的"子女"或"孩子"，同一结点的"子女"之间互称"兄弟"。

二叉树：二叉树是一种十分重要的树型结构。它的特点是，树中的每个结点最多只有两棵子树，即树中任何结点的度数不得大于２。二叉树的子树有左右之分，而且，子树的左右次序是重要的，即使在只有一棵子树的情况下，也应分清是左子树还是右子树。定义：二叉树是结点的有限集合，这个集合或是空的，或是由一个根结点和两棵互不相交的称之为左子树和右子树的二叉树组成。

（三）完全二叉树

对满二叉树，从第一层的结点(即根)开始，由下而上，由左及右，按顺序结点编号，便得到满二叉树的一个顺序表示。据此编号，完全二叉树定义如下：一棵具有ｎ个结点，深度为K的二叉树，当且仅当所有结点对应于深度为K的满二叉树中编号由１至ｎ的那些结点时，该二叉树便是完全二叉树。图4是一棵完全二叉树。

平衡二叉树

当且仅当两个子树的高度差不超过1时，这个树是平衡二叉树。（同时是排序二叉树）

平衡二叉树，又称AVL树。它或者是一棵空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的高度之差之差的绝对值不超过1.。

常用算法有：红黑树、AVL树、Treap等。

平衡二叉树的调整方法

平衡二叉树是在构造二叉排序树的过程中，每当插入一个新结点时，首先检查是否因插入新结点而破坏了二叉排序树的平衡性，若是，则找出其中的最小不平衡子树，在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。具体步骤如下：

⑴ 每当插入一个新结点，从该结点开始向上计算各结点的平衡因子，即计算该结点的祖先结点的平衡因子，若该结点的祖先结点的平衡因子的绝对值均不超过1，则平衡二叉树没有失去平衡，继续插入结点；

⑵ 若插入结点的某祖先结点的平衡因子的绝对值大于1，则找出其中最小不平衡子树的根结点；

⑶ 判断新插入的结点与最小不平衡子树的根结点的关系，确定是哪种类型的调整；

⑷ 如果是LL型或RR型，只需应用扁担原理旋转一次，在旋转过程中，如果出现冲突，应用旋转优先原则调整冲突；如果是LR型或LR型，则需应用扁担原理旋转两次，第一次最小不平衡子树的根结点先不动，调整插入结点所在子树，第二次再调整最小不平衡子树，在旋转过程中，如果出现冲突，应用旋转优先原则调整冲突；

⑸ 计算调整后的平衡二叉树中各结点的平衡因子，检验是否因为旋转而破坏其他结点的平衡因子，以及调整后的平衡二叉树中是否存在平衡因子大于1的结点。

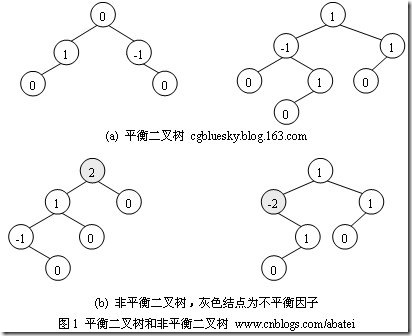
（b）左边的图 左子数的高度为3，右子树的高度为1，相差超过1

（b）右边的图 -2的左子树高度为0  右子树的高度为2，相差超过1

 

完全二叉树(Complete Binary Tree)

 

完全二叉树定义

 

完全二叉树

若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层从右向左连续缺若干结点，这就是完全二叉树。

完全二叉树特点

一、叶子结点只可能在最大的两层上出现,对任意结点，若其右分支下的子孙最大层次为L，则其左分支下的子孙的最大层次必为L 或 L+1；

二、出于简便起见,完全二叉树通常采用数组而不是链表存储,其存储结构如下:

var tree:array[1..n]of longint;{n:integer;n>=1}

对于tree[i]，有如下特点：

（1）若i为奇数且i>1，那么tree[i]的左兄弟为tree[i-1]；

（2）若i为偶数且i<n，那么tree[i]的右兄弟为tree[i+1]；

（3）若i>1，tree[i]的双亲为tree[i div 2]；

（4）若2*i<=n，那么tree[i]的左孩子为tree[2*i]；若2*i+1<=n，那么tree[i]的右孩子为tree[2*i+1]；

（5）若i>n div 2,那么tree[i]为叶子结点（对应于（3））；

（6）若i<(n-1) div 2.那么tree[i]必有两个孩子（对应于（4））。

特别地：满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

完全二叉树叶子节点的算法

如果一棵具有n个结点的深度为k的二叉树，它的每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应，这棵二叉树称为完全二叉树。

可以根据公式进行推导，假设n0是度为0的结点总数（即叶子结点数），n1是度为1的结点总数，n2是度为2的结点总数，由二叉树的性质可知：n0＝n2＋1，则n= n0＋n1＋n2（其中n为完全二叉树的结点总数），由上述公式把n2消去得：n= 2n0+n1－1，由于完全二叉树中度为1的结点数只有两种可能0或1，由此得到n0＝（n＋1）/2或n0＝n/2，合并成一个公式：n0＝（n＋1）/2 ，就可根据完全二叉树的结点总数计算出叶子结点数。

满二叉树

一棵深度为k，且有2的(k)次方－1个节点的二叉树 特点：每一层上的结点数都是最大结点数

完全二叉树的定义：深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时，称为完全二叉树。 特点：叶子结点只可能在层次最大的两层上出现；对任一结点，若其右分支下子孙的最大层次为l，则其左分支下子孙的最大层次必为l 或l+1 满二叉树：一棵深度为k，且有2的(k)次方－1个节点的二叉树 特点：每一层上的结点数都是最大结点数 满二叉树肯定是完全二叉树完全二叉树不一定是满二叉树