csapp_02读书笔记：信息的表示和处理

一、 整数

1.1 无符号数编码

对于向量$\vec{x}=\left[x_{w-1},x_{w-2},...,x_0\right]$而言，函数$B2U_w$(Binary to Unsigned)负责将$\vec{x}$所代表的0，1序列映射为无符号整数：
$$B2U_w(\vec{x})=\sum _{i=0}^{w-1}{x}_i\cdot 2^i$$
下面例子展示了$B2U_w$对于位向量的操作：
$$\begin{gathered} B2U_4([0001])=0\cdot 2^3+0\cdot 2^2+0\cdot 2^1+1\cdot 2^0=1 \\ B2U_4([1111])=1\cdot 2^3+1\cdot 2^2+1\cdot 2^1+1\cdot 2^0=15 \end{gathered}$$

1.2 有符号数编码

我们用函数$B2T_w$（Binary To Two's-completement）来表示将位向量来映射为有符号数的操作：
$$B2T_w(\vec{x})=-x_{w-1}\cdot 2^{w-1}+\sum _{i=0}^{w-2}{x}_i\cdot 2^i$$
下面例子展示了$B2T_w$对于位向量的操作：
$$\begin{gathered} B2T_4([0001])=-0\cdot 2^3+0\cdot 2^2+0\cdot 2^1+1\cdot 2^0=1 \\ B2T_4([1111])=-1\cdot 2^3+1\cdot 2^2+1\cdot 2^1+1\cdot 2^0=-1 \end{gathered}$$

1.3 补码转无符号数

$$T2U_w(x)=\{\begin{array}{ll}x+2^w& ,x<0\\ x& ,x\ge 0\end{array}$$
比如
$$T2U_4(-1)=-1+2^4=15$$

1.4 无符号数转补码

$$U2T_w(u)=\{\begin{array}{ll}u& ,u\le TMa{x}_w\\ u-2^w& ,u>TMa{x}_w\end{array}$$
比如

$$U2T_w(15)=15-16=-1$$

二、整数运算

三、浮点数

其实，浮点数是采用科学计数法的方式来表示的，例如十进制小数 8.345，用科学计数法表示，可以有多种方式：

8.345 = 8.345 * 10^0
8.345 = 83.45 * 10^-1
8.345 = 834.5 * 10^-2
...

看到了吗？用这种科学计数法的方式表示小数时，小数点的位置就变得「漂浮不定」了，这就是相对于定点数，浮点数名字的由来。

3.1 浮点数如何表示数字？

我们已经知道，浮点数是采用科学计数法来表示一个数字的，它的格式可以写成这样：

V = (-1)^S * M * R^E

其中各个变量的含义如下：

• S: 取值0或1，表示一个数的正负
• M: 尾数，用小数表示，比如8.345 * 10^0，8.35就是尾数
• R: 基数，表示十进制就是10，表示二进制就是2
• E: 阶数，用整数表示，比如834.5 * 10^-2，-2就是阶数

如果我们要在计算机中，用浮点数表示一个数字，只需要确认这几个变量即可。

假设现在我们用 32 bit 表示一个浮点数，把以上变量按照一定规则，填充到这些 bit 上就可以了：

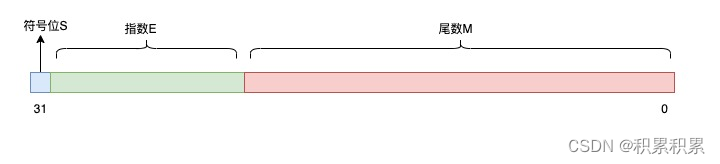
假如我们定义如下规则来填充这些位：

• 符号位S占1bit
• 指数E占10bit
• 尾数M占21bit

按照这个规则，将十进制数25.125转换为浮点数，转换过程就是这样的（D代表十进制，B代表二进制）：

1. 整数部分：25(D)=11001
2. 小数部分：0.125(D)=0.001
3. 用二进制科学计数法表示：25.125(D)=11001.001(B)=1.1001001 * 2^4(B)

所以，符号位S=0,尾数M=11001.001(B)

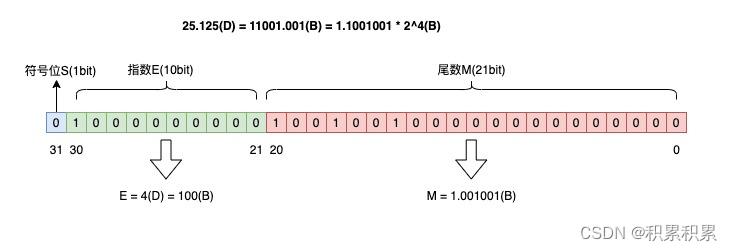
3.2 浮点数标准

1985年，IEEE 组织推出了浮点数标准，就是我们经常听到的 IEEE754 浮点数标准，这个标准统一了浮点数的表示形式，并提供了 2 种浮点格式：

• 单精度浮点数 float：32 位，符号位 S 占 1 bit，指数 E 占 8 bit，尾数 M 占 23 bit
• 双精度浮点数 float：64 位，符号位 S 占 1 bit，指数 E 占 11 bit，尾数 M 占 52 bit

为了使其表示的数字范围、精度最大化，浮点数标准还对指数和尾数进行了规定：

1. 尾数M的第一位总是1（因为1 <= M < 2），因此这个1可以省略不写，它是个隐藏位，这样单精度23位尾数可以表示了24位有效数字，双精度52位尾数可以表示 53位有效数字
2. 指数E是无符号整数，表示float时一共占8位，所以它的取值范围为0~255。但是因为指数可以是负的，所以规定存入E的时候需要加上一个中间数127，这样E的取值范围为-127 ~ 128。表示double时，一共占11 bit，存入E时加上中间数1023，这样取值范围为-1023 ~ 1024。

除了规定尾数和指数位，还做了以下规定：

• 指数 E 非全 0 且非全 1：规格化数字，按上面的规则正常计算
• 指数 E 全 0，尾数非 0：非规格化数，尾数隐藏位不再是 1，而是 0(M = 0.xxxxx)，这样可以表示 0 和很小的数
• 指数 E 全 1，尾数全 0：正无穷大/负无穷大（正负取决于 S 符号位）
• 指数 E 全 1，尾数非 0：NaN(Not a Number)

打印浮点数bit位：

void print_flot_bit(float *fp){
  // 1. print S 
  uint32_t* uip32 = (uint32_t*)fp;
  printf("S=%u\n", (*uip32) >> 31);
  // 2. print E
  printf("E=");
  for(int i=30; i>=23; i--){
    printf("%d", ((*uip32) >> i) & 1);
  }
  printf("\n");
  // 3. print M 
  printf("M=");
  for(int i=22; i>=0; i--){
    printf("%d", ((*uip32) >> i) & 1);
  }
  printf("\n");
}

3.3 浮点数为什么会有精度损失

我们再来看一下，平时经常听到的浮点数会有精度损失的情况是怎么回事？

如果我们现在想用浮点数表示 0.2，它的结果会是多少呢？

0.2 转换为二进制数的过程为，不断乘以 2，直到不存在小数为止，在这个计算过程中，得到的整数部分从上到下排列就是二进制的结果。

0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0（发生循环）
...

所以0.2(D)=0.00110(B)...。

因为10进制的0.2无法精确转成二进制小数，而计算机再表示一个小数时，宽度是有限的，无限循环的小数存储在计算机的时候只能被截断，所以就会导致小数精度发生损失的情况

int main(int argc, char *argv[]) {
  float f = 0.2;
  printf("%.10f\n", f);	// 0.2000000030
  return 0;
}

3.4 精度

float和double的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的，其整数部分始终是一个隐含着的“1”，由于它是不变的，故不能对精度造成影响。

float：2^23 = 8388608，一共七位，这意味着最多能有7位有效数字，但绝对能保证的为6位，也即float的精度为6~7位有效数字；
double：2^52 = 4503599627370496，一共16位，同理，double的精度为15~16位。

参考

1. csapp重点阅读
2. csdn数学公式
3. csapp实验环境搭建
4. 读薄 CSAPP： 数据表示
   
5. 数学符号：累加，累乘
6. latex在线
7. latex求和符号
8. 计算机系统基础（四）浮点数
9. 浮点数精度丢失
10. IEEE754浮点数在线转化
11. 逻辑代数与逻辑函数
12. csapp_lab01-b站
13. lab官方地址
14. lab参考推荐
15. b站视频-原版翻译
16. b站视频-讲解
17. 非规格化数字的范围