概率论与数理统计-第二章 随机变量及其分布

第二章 随机变量及其分布

2.1 随机变量

定义

设随机试验的样本空间S，称定义在样本空间S上的实值单值函数X=X(ω)为随机变量
将事件A={ω|X(ω)=a}记为{X=a}.（ω为样本点）
随机变量就是给样本点一个数字代表
分类：离散型（有限个、无限可列个）、非离散型（连续型）

2.2离散型随机变量及其概率分布

一、离散型随机变量及其概率分布

• 定义1：设离散型随机变量X的所有可能取值为x_i($i$=1,2,…)
  P{X=$x$_i}=p_i, $i$=1,2,…
  称为X的概率分布或分布律，也称概率函数
• 常用表格形式来表示X的概率分布：
  由概率的定义，p_i(i=1,2,…)必然满足：
  (1)p_i≥0，i=1,2,…;
  (2)∑_ip_i=1.
• 例题
  

二、常用离散分布

• 1. 两点分布（X~B/b(1,p)）
  • 定义2：若一个随机变量X只有两个可能取值，且其分布为
    P{X=x₁}=p,P{X=x₂}=1-p(0<p<1)
    则称X服从x₁,x₂处参数为p的两点分布
    P{X=k}=p^k(1-P)^1-k,k=0,1,
  • 特别地，若X服从x₁=1,x₂=0处参数为p的两点分布，即
    
    则称X服从参数为p的0-1分布，其中q=1-p.
    易见，(1)0<p,q<1;(2)p+q=1.

• 几何分布
  第k次首次发生，前k-1次未发生
  P{x=k}=(1-p)^k-1 p, X~G( p ) k = 1,2,3…

• 2. 二项分布（X~B/b(n,p)）
  • 在n重伯努利试验中，设每次试验中事件A发生的概率为p.用X表示n重伯努利试验中事件A发生的次数，则X的可能取值为0,1，… ，n,且对每一个k(0≤k≤),事件{X=k}即为“n次试验中事件A恰好发生k次”.根据伯努利概型，有
    P{X=k}=C_n^k p^k(1-p)^n-k, k=0,1,…,n. (2.1)
    当n=1时，式(2.1)变为
    P{X=k}=p^k(1-p)^1-k, k=0,1.
    此时，随机变量X即服从0-1分布，
  • 定义3若一个随机变量X的概率分布由式(2.1)给出，则称X服从参数为n,p的二项分布.记为X~b(n,p)(或B(n,p)
    显然，(1)P{X=k}≥0；(2)∑ⁿ_k=0P{X=k}=1.
  • 二项分布的图形特点：
    
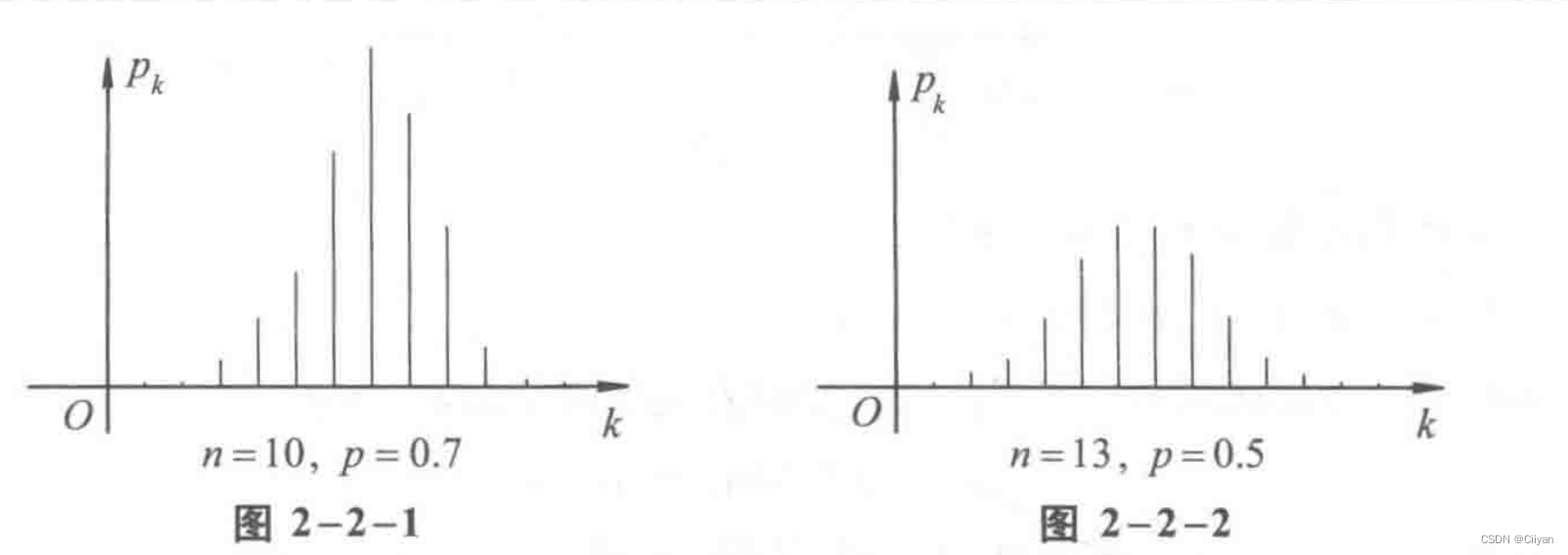
    从图中可看出：对于固定的n及p,当k增加时，概率P{X=k}先是随之增加直至达到最大值，随后单调减少.可以证明，一般的二项分布的图形也具有这一性质.且
    (1)当(n+1)p不为整数时，二项概率P{X=k}在k=[(n+1)p]时达到最大值；
    (2)当(n+1)p为整数时，二项概率P{X=k}在k=(n+1)p和k=(n+1)p-1时达到最大值，
    

3. 泊松分布(X~P/π(λ))
   定义4若一个随机变量X的概率分布为
   
   则称X服从参数为λ的泊松分布，记为X~ P(λ)（或X~ π(λ)).
   易见，(1)P{X=k}≥0，k=0,1,2,…;
   （2）
   例5某城市每天发生火灾的次数X服从参数入=0.8的泊松分布，求该城市一
   天内发生3次或3次以上火灾的概率
   解：由概率的性质及式(2.2)，得
   P{X≥3}
   =1-P{X<3}
   =1-P{X=0}-P{X=1}-P{X=2}
   =1-e^-0.8(0.8⁰/0!+0.8¹/1!+0.8²/2!)
   ≈0.0474.

2.3 随机变量的分布函数

一、随机变量的分布函数

• 定义1设X是一个随机变量，称
  F(x)=P{X ≤ x} (-∞ < x < +∞)）
  为X的分布函数，有时记作X~ F(x)或F_X(x).
• 分布函数的性质：
  (1)单调非减.若x1<x2,则F(x1)≤F(x2):
  (2)F(-∞)=lim_x->-∞ F(x)=0, F(+∞)=lim_x->+∞ F(x)=1.
  (3)右连续性.即lim（x→x⁺₀） F(x)=F(x₀),
  
  

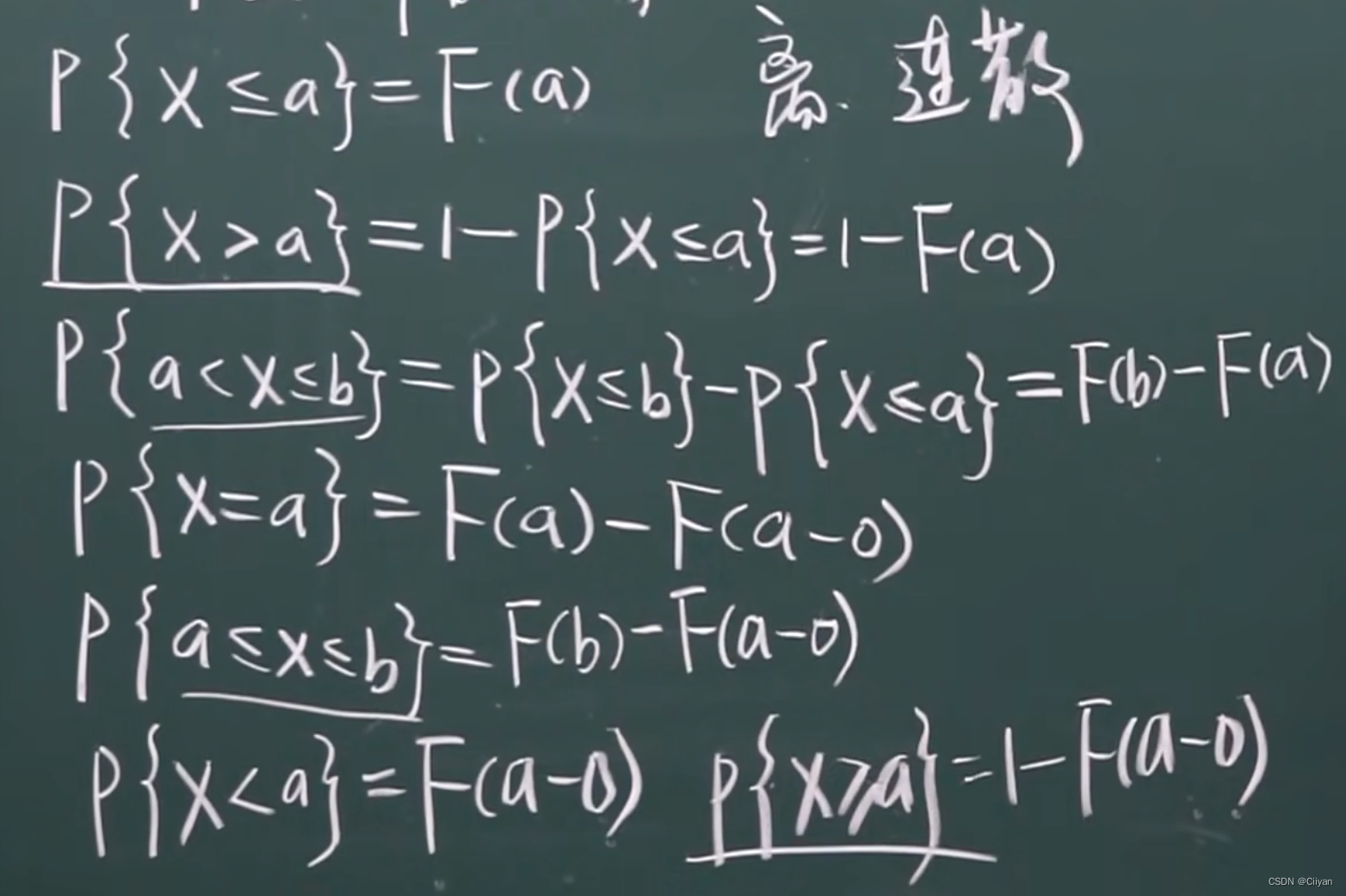
二、离散型随机变量的分布函数

设离散型随机变量X的概率分布为

则X的分布函数为
F(x)=P{X≤x}=∑(x_i<=x) P{X=x_i}=∑(x_i<=x) p_i
如图2-3-1所示，F(x)是一个阶梯形函数，它在点x=x_i(i=1,2,…)处有跳跃，跃度恰为随机变量X在点x=x_i处的概率p_i=P{X=x_i}

若一个随机变量X的分布函数为阶梯形函数，则X一定是一个离散型随机变量，其概率分布亦由F(x)唯一确定

2.4 连续型随机变量及其概率密度

一、连续型随机变量及其概率密度

• 定义1: 如果对随机变量X的分布函数F(x),存在非负可积函数f(x),使得对于任意实数x,有
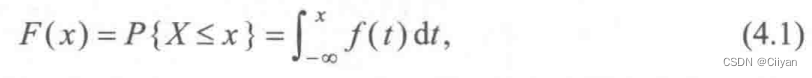
  则称X为连续型随机变量，称f(x)为X的概率密度函数，简称为概率密度或密度函数.
• 密度函数的性质：
  (1)f(x)≥0；
  
  (2)对一个连续型随机变量X,若已知其密度函数f(x),则根据定义，可求得X的取值落在任意区间(a,b]上的概率
  （3）连续型随机变量的取值落在实数轴上任一区间内的概率都等于密度函数在该区间上的积分。
  （4）连续型随机变量X取任一指定值a(a∈R)的概率为0.因为
  
  故对连续型随机变量X,有
  
  (5)若f(x)在点x处连续，则
  

二、常用连续型分布

1. 均匀分布（X~U(a,b)）

• 定义2：若连续型随机变量X的概率密度为
  则称X在区间(a,b)上服从均匀分布，记为X~U(a,b).
  易见(1)f(x)≥0；
• X的分布函数为
  

2. 指数分布(X~e(λ))
   若随机变量X的概率密度为
   则称X服从参数为入的指数分布.简记为X~e(λ)
   易见(1)f(x)≥0；

若X服从参数为入的指数分布，易求出其分布函数

3.正态分布（X~N(μ，σ²)）
定义4若随机变量X的概率密度为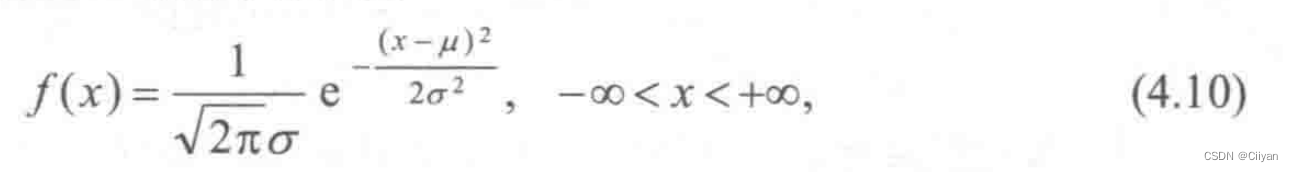
则称X服从参数为μ和σ2的正态分布，记为X~N(μ,σ2)，其中(μ和σ(σ>0)都是常数.
易见(1)f(x)≥0；
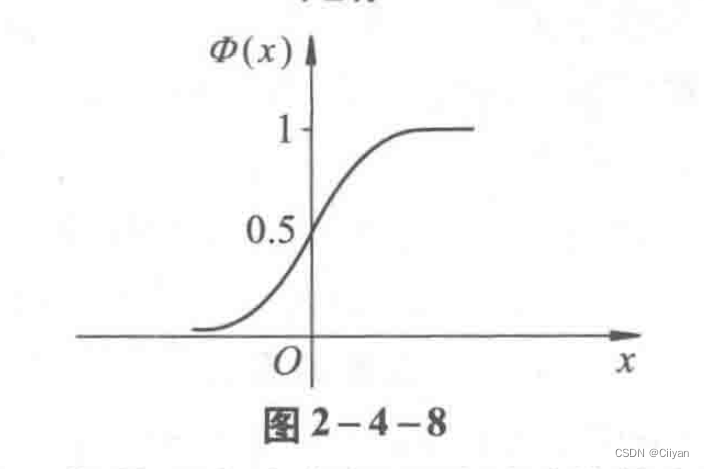
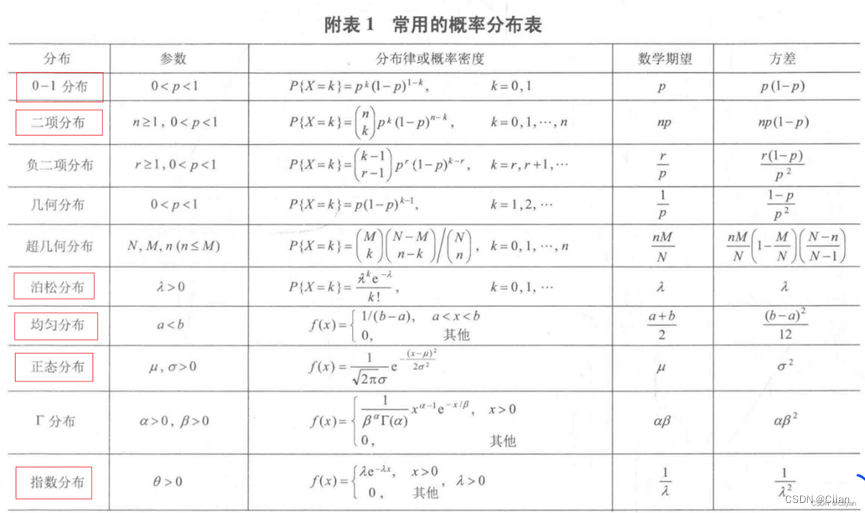
当μ=0，σ=1时，正态分布称为标准正态分布，此时，其密度函数和分布函数
常用φ(x)和Φ(x)表示（见图2-4-7和图2-4-8）.

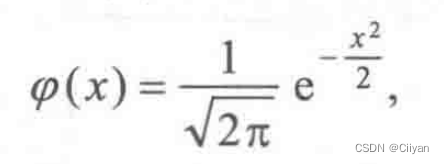
定理1设X~ N(u,σ²),则

结：F(x)=P(X<=x); P(x) = 0;

2.5 随机变量函数的分布

一、随机变量的函数

己知：若随机变量X~N(μ,σ2)，则随机变量
这里，Y是随机变量X的函数，对于X的每一个取值，Y有唯一确定的取值与之对应.由于X是随机变量，其取值事先不确定，因而Y的取值也随之不确定，即Y也是随机变量.
定义1：如果存在一个函数g(x),使得随机变量X,Y满足Y=g(X),则称随机变量Y是随机变量X的函数.

二、离散型随机变量函数的分布

设离散型随机变量X的概率分布为P{X=x}=p_i,i=1,2,…,
易见，X的函数Y=g(X)显然还是离散型随机变量

三、连续型随机变量函数的分布

• 例2 设随机变量X~N(0,1),Y=e^X,求Y的概率密度函数.
  解设F_Y(y),f_Y(y)分别为随机变量Y的分布函数和概率密度函数，则当y≤0时，有
  F_Y(y)=P{Y≤y}=P{e^x≤y}=P{Ø}=0.
  当y>0时，因为g(x)=e^x是x的严格单调增函数，所以有{e^x≤y}={X≤lny},
  因而F_Y(y)=P{Y≤y}=P{e^X≤y}=P{X≤lny}=
  再由f_Y(y)=F’_Y(y),得
  通常称上式中的Y服从对数正态分布，它也是一种常用的寿命分布

• 例4设随机变量X~N(μ,σ²)，试证明X的线性函数Y=aX+b(a≠0)也服从正态分布：
  Y=aX+b ~ N(aμ+b,(aσ)²).
  特别地，若在本例中取a=1/σ,b=-μ/σ，则得~N(0,1)

分布函数F_X(x),F_Y(x)
概率密度函数f_X(x),f_Y(x)
X服从[a,b]均匀分布，Y=kx +C(k≠0)服从相应区间上的均匀分布

• 定理2： X的密度函数f_X(x) , Y=kX+b(k≠0)，f_Y(X)=
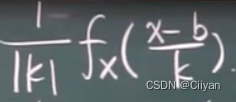
  积分变限函数求导【∫^φ(x) _ψ(x) f(t)dt】’ = f(φ(x))φ’(x)-f(ψ(x))ψ’(x)