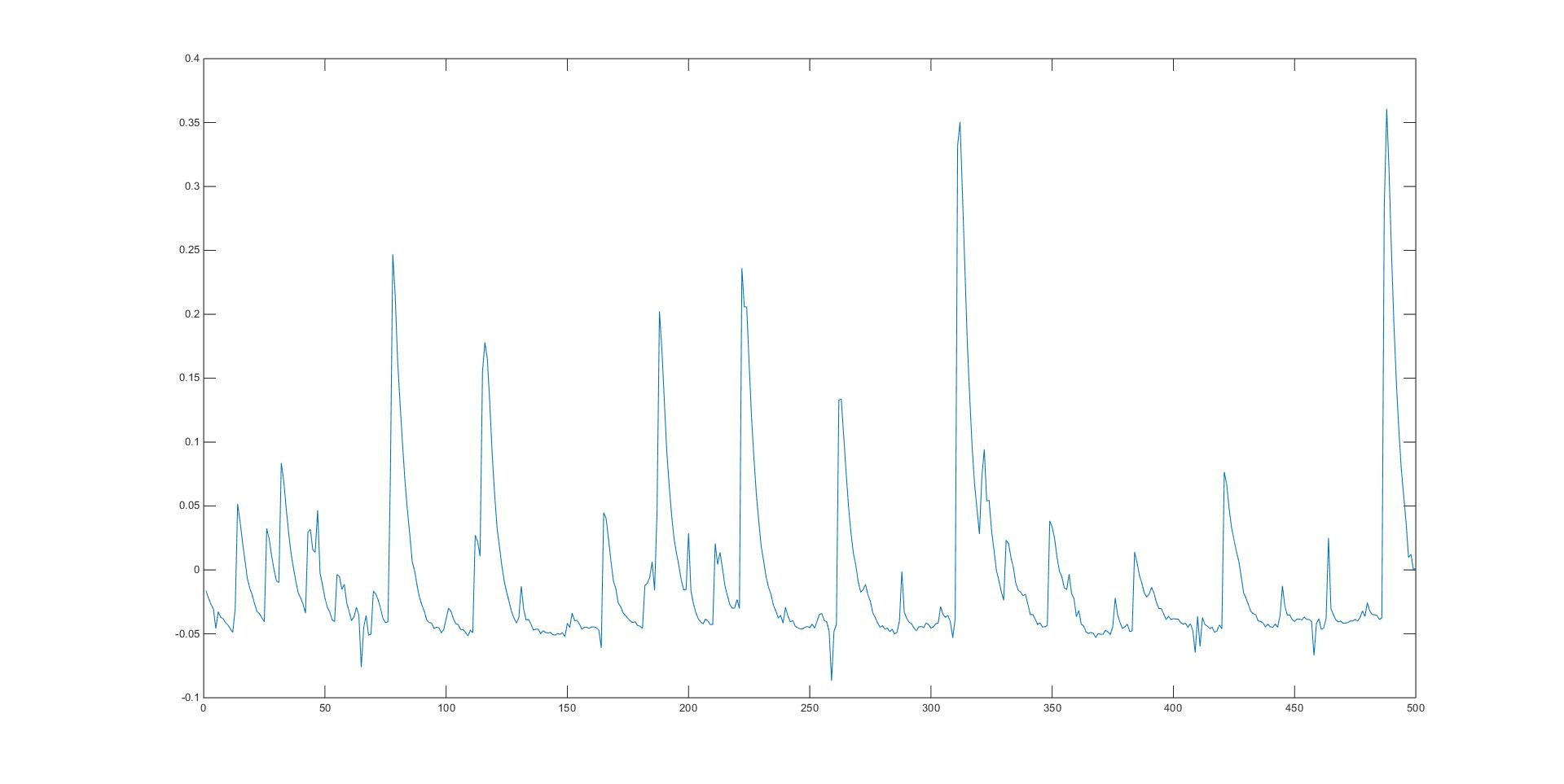
现有的数据是有探测器测得的脉冲信号,需要对其发生时间进行一个估计。
主要思想是,通过hist方法将不同时间间隔出现的次数进行一个计数。
经过统计可以得到
[1.4000000e+013.2000000e+01,7.8000000e+01,1.1600000e+02,1.8800000e+02,2.2200000e+02,2.6300000e+02,3.1200000e+02,3.2200000e+02,4.2100000e+02,4.8800000e+02,5.0400000e+02,5.1900000e+02,5.7200000e+02,7.2600000e+02,9.4500000e+02,1.0100000e+03,1.0650000e+03,1.1900000e+03]
这些位置出现了脉冲峰,需要验证它们之间出现的间隔分布。
第一步,读取脉冲位置并计算脉冲间时间间隔
def read_diff():
d = pd.read_table('data/peaks.csv', names=['pks', 'locs', 'None'], delim_whitespace=True)
time = d['locs']
dif = []
for i, ele in enumerate(time[1:]):
dif.append(ele - time[i])
return dif使用pandas的read_table方法,由于是在win平台下,各种格式问题,导致读入后会出现三列(应该为峰值一列,位置一列),最后一列应该为win下的’\t’,想着不碍事,就没仔细研究。
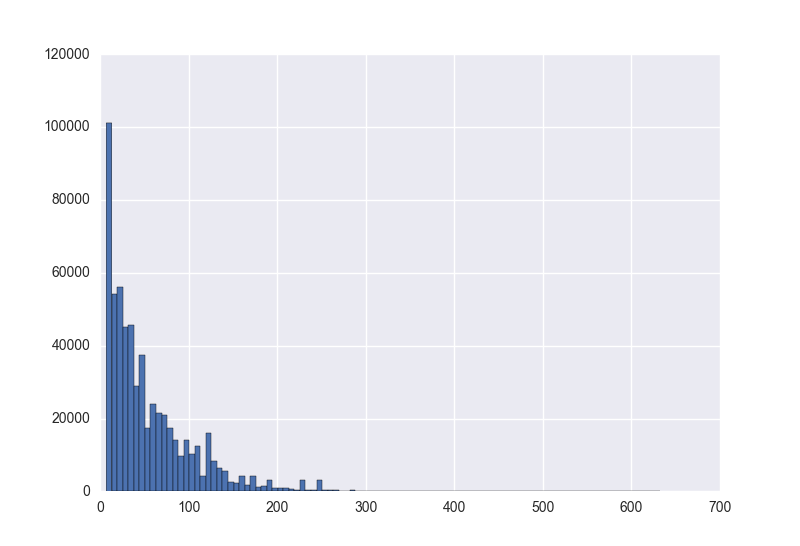
第二步,对间隔频率进行统计
对时间间隔进行统计可以直接使用Pandas.Series的的hist方法,也可以使用pylab中的hist方法。
其实Pandas中的画图方法也是调用的matplotlib,都可以在画出直方图的同时进行密度估计,但是这两个方法有一个最大的区别就是,pylab中的hist可以指定一个range参数.
```matplotlib.pyplot.hist(x, bins=10, range=None, normed=False, weights=None, cumulative=False, bottom=None, histtype='bar', align='mid', orientation='vertical', rwidth=None, log=False, color=None, label=None, stacked=False, hold=None, data=None, **kwargs)
range : tuple or None, optional
The lower and upper range of the bins. Lower and upper outliers are ignored. If not provided, range is (x.min(), x.max()). Range has no effect if bins is a sequence.
If bins is a sequence or range is specified, autoscaling is based on the specified bin range instead of the range of x.
Default is None```
import matplotlib.pylab as plt
cnt = plt.hist(dif, bins=bin)其中cnt[0]为计数值y,cnt[1]为坐标x
第三步,对已得的频率分布做概率密度估计
Plan A
使用scipy.optimize中的最小二乘拟合
import numpy as np
from scipy.optimize import leastsq
def func_n(x, a, b, c):
return a * np.square(x) + b * x + c
def residuals(p, x, y, reg):
regularization = 0.1 # 正则化系数lambda
ret = y - func_n(x, p)
if reg == 1:
ret = np.append(ret, np.sqrt(regularization) * p)
return ret
def diff_time(bin=50, reg=1):
d = pd.read_table('data/peaks.csv', names=['pks', 'locs', 'None'], delim_whitespace=True)
time = d['locs']
dif = []
for i, ele in enumerate(time[1:]):
dif.append(ele - time[i])
plt.figure()
cnt = plt.hist(dif, bins=bin)
x = cnt[1]
y = cnt[0]
try:
r = leastsq(residuals, [1, 1, 1], args=(x, y, reg))
except:
print("Error - curve_fit failed")
y2 = [func(i, r[0]) for i in x]
plt.plot(x, y2)因为之前用过该方法,所以想用使用二次多项函数来拟合,结果总是抛出异常Error - curve_fit failed。
不过也是,别人明明是一个类指数函数,你非要哪个二次多项函数来拟合=。=
Plan B
在查阅一番以后,发现,对于这类函数拟合的话,from scipy.optimize import curve_fit这个对于高斯型、指数型函数拟合效果比较好
[curve_fit]
def kde_sim(bins=150):
dif = read_diff()
plt.figure()
cnt = plt.hist(dif, bins=bins)
x = cnt[1]
y = cnt[0]
popt, pcov = curve_fit(func, x[1:], y)
y2 = [func(i, popt[0], popt[1], popt[2]) for i in x]
plt.figure()
plt.plot(x, y2, 'r--')
return popt然而效果也不是很好。。。
Plan C
正在我踌躇之际,发现了一个新大陆,Seaborn,这模块简直叫个好用,图画出来好看不说,速度还很快,还简单,对于画这种概率分布的图简直不要太爽。displot
sns.distplot(data)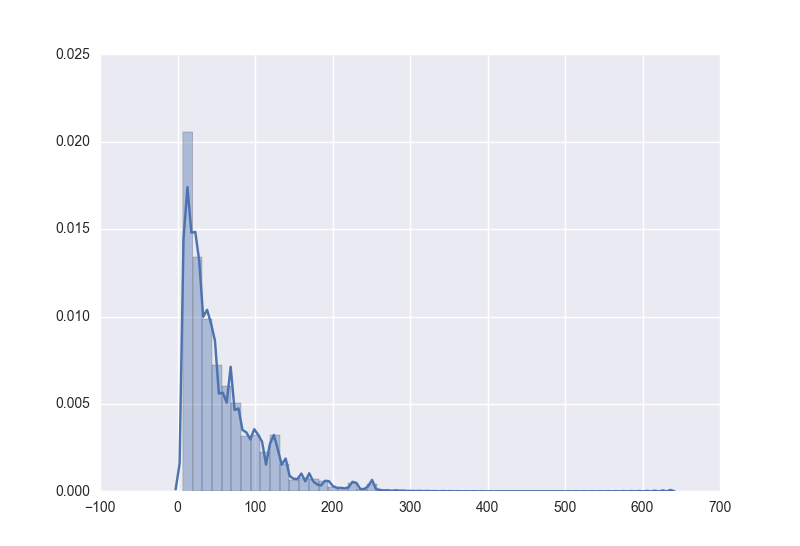
除了可以对曲线概率密度进行估计外,还可以使用指定函数进行拟合
from scipy import stats
sns.distplot(d,kde=False, fit=stats.expon)第四步 得到其概率密度函数
Plan A 使用scipy.stats模块
scipy.stats
在该模块中有两大通用分布类应用在连续随机分布变量和离散随机分布变量。
超过80种连续分布和10中离散分布。在这之外,可以由用户自己创建新的分布
针对连续变量的主要方法有:
Rvs:随机变量
Pdf:概率密度函数
Cdf:累计分布函数
Sf:残差函数
Ppf:百分点函数,cdf/1
Isf:1/sf
不过..首先其文档对我这种六级低空飘过的人来说读着好烦恼,所以,对其参数设置什么的不是很理解,从而导致得到的pdf(概率密度函数)效果不是很好。
Plan B 继续使用Seaborn模块
后来我转念一想,seaborn返回的图中,拟合的函数都很好的,seaborn内部肯定有估计后的函数模型,我直接加一个模型输出不就好了,于是我就从github上把源码下了下来。
在displot模块中,对matplotlib做了很多的加工,在函数拟合方面使用的是
statsmodels和scipy.stats.gaussian_kde这两个模块,优先使用的是statsmodels
distplot里关于拟合的代码如下
if fit is not None:
fit_color = fit_kws.pop("color", "#282828")
gridsize = fit_kws.pop("gridsize", 200)
cut = fit_kws.pop("cut", 3)
clip = fit_kws.pop("clip", (-np.inf, np.inf))
bw = stats.gaussian_kde(a).scotts_factor() * a.std(ddof=1)
x = _kde_support(a, bw, gridsize, cut, clip)
params = fit.fit(a) #stats中分布具有fit方法
pdf = lambda x: fit.pdf(x, *params) #由参数得到概率密度函数
y = pdf(x) #得到y向量
if vertical:
x, y = y, x
ax.plot(x, y, color=fit_color, **fit_kws)
if fit_color != "#282828":
fit_kws["color"] = fit_color通过该模块调用得到的概率密度obj有以下方法
Methods
cdf() Returns the cumulative distribution function evaluated at the support.
cumhazard() Returns the hazard function evaluated at the support.
entropy() Returns the differential entropy evaluated at the support
evaluate(point) Evaluate density at a single point.
fit([kernel, bw, fft, weights, gridsize, ...]) Attach the density estimate to the KDEUnivariate class.
icdf() Inverse Cumulative Distribution (Quantile) Function
sf() Returns the survival function evaluated at the support.通过scipy.stats.gaussian_kde调用得到的kde对象有以下属性和方法(这里我就不翻译了)
Attributes
dataset (ndarray) The dataset with which gaussian_kde was initialized.
d (int) Number of dimensions.
n (int) Number of datapoints.
factor (float) The bandwidth factor, obtained from kde.covariance_factor, with which the covariance matrix is multiplied.
covariance (ndarray) The covariance matrix of dataset, scaled by the calculated bandwidth (kde.factor).
inv_cov (ndarray) The inverse of covariance.
Methods
kde.evaluate(points) (ndarray) Evaluate the estimated pdf on a provided set of points.
kde(points) (ndarray) Same as kde.evaluate(points)
kde.integrate_gaussian(mean, cov) (float) Multiply pdf with a specified Gaussian and integrate over the whole domain.
kde.integrate_box_1d(low, high) (float) Integrate pdf (1D only) between two bounds.
kde.integrate_box(low_bounds, high_bounds) (float) Integrate pdf over a rectangular space between low_bounds and high_bounds.
kde.integrate_kde(other_kde) (float) Integrate two kernel density estimates multiplied together.
kde.resample(size=None) (ndarray) Randomly sample a dataset from the estimated pdf.
kde.set_bandwidth(bw_method=’scott’) (None) Computes the bandwidth, i.e. the coefficient that multiplies the data covariance matrix to obtain the kernel covariance matrix. .. versionadded:: 0.11.0
kde.covariance_factor (float) Computes the coefficient (kde.factor) that multiplies the data covariance matrix to obtain the kernel covariance matrix. The default is scotts_factor. A subclass can overwrite this method to provide a different method, or set it through a call to kde.set_bandwidth.所以,如果想获取概率分布,直接return pdf
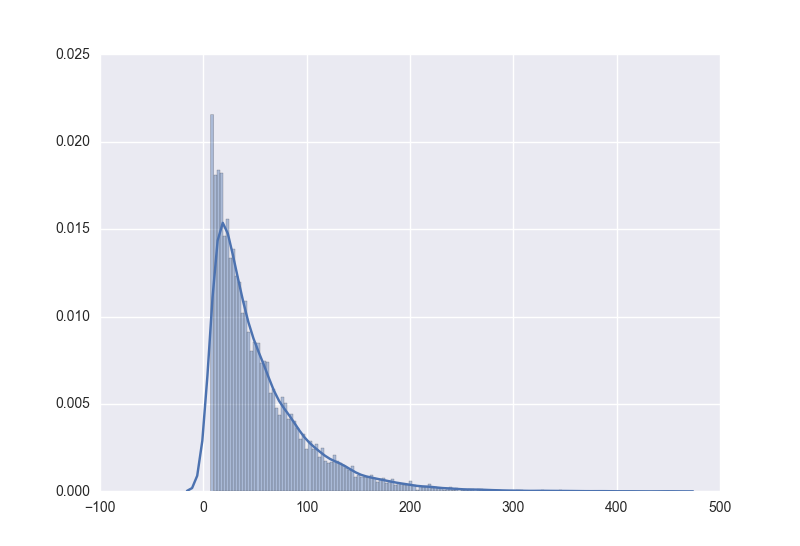
其中,使用
sns.distplot(data, bins=150, kde=True)时得到的模型进行resample同样数据量得到的hist图形为
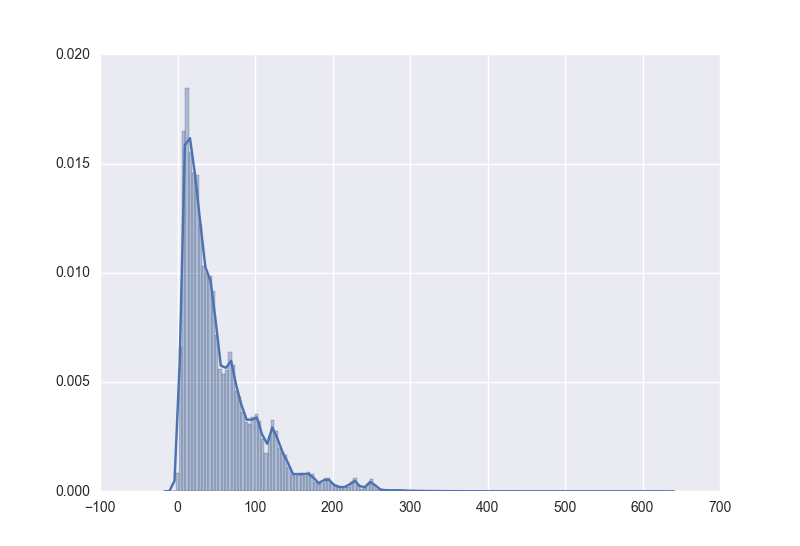
当resample的数量较小时,因为噪声的缘故反而比较接近原始分布
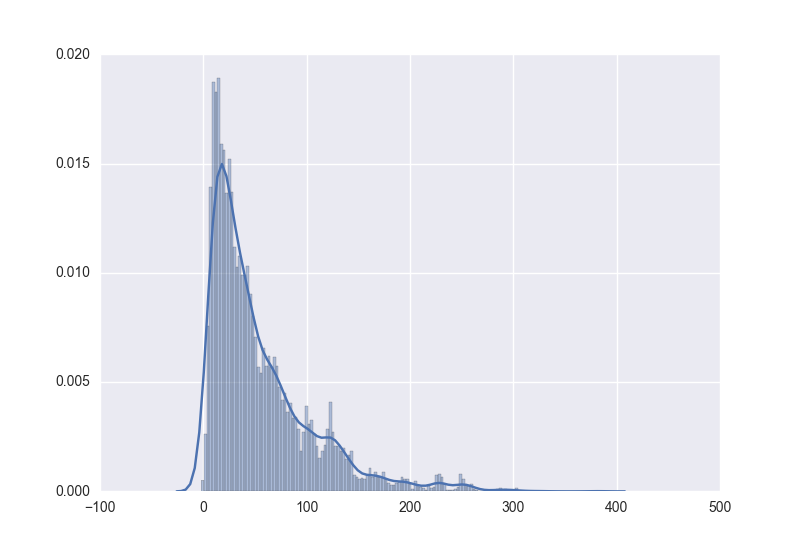
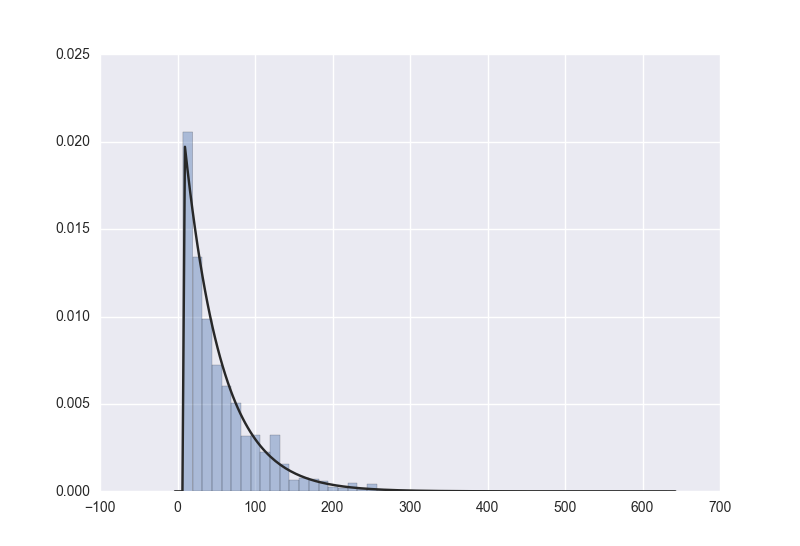
而使用
from scipy import stats
sns.displot(data, bins=150, kde=False, fit=stats.expon)时,是将数据拟合成一个指数函数,运用该模型resample同样数据得到的数据hist图形为
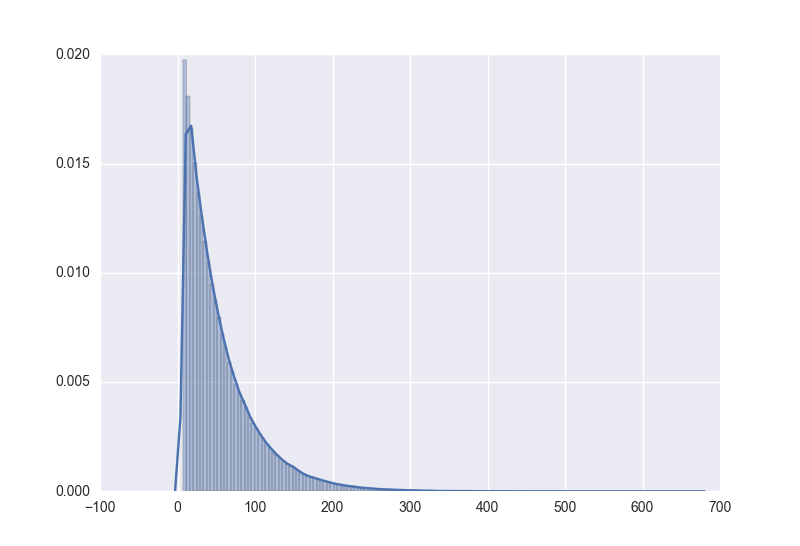
fit后使用较少数量的样本值同样也是
有一个问题就是,在原数据中,是从大于0的某个值开始hist的,但在resample的数据中,出现了一个较小的值甚至是负值,这个还不知道是否会给接下来的工作造成影响….先这样吧,如果要求比较严的话,就只能回来再改动了。
























 4409
4409











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








