结构的艺术：模糊查询

系统的学过编程的人应该都知道，有一门基础课：《数据结构与算法》，这门课很重要，但是许多人却不怎么重视，导致后来算法学习频频碰壁。我不会给大家系统的讲数据结构，但是我会给大家讲一些很有趣的结构，下来的学习还是得靠大家自己努力啦。
这次讲的是模糊查询，在模糊查询之前，我们先看一下如何精确查询。
比如我想要在一堆(n个)字符串里查找我的名字‘liuruiyang’，那么我需要和这堆(n个)字符串里的每个字符串作比较，而每次比较时间复杂度都是O(len)，所以总的时间复杂度就是O(n*len)；
既然精确查询如此，模糊查询也不会差太多，模糊查询，当你查询‘liu’时，会出现所有开头为‘liu’的字符串，既然这样，我依然要跟每个字符串作比较，总的时间复杂度依然是O(n*len)；
我们知道，英文字母有26个，不考虑大小写和符号的话，我们使用26个字母就可以表示所有的单词，那么对于一个单词而言，这个单词由字母组成，那么每个单词就由两部分组成：
①：单词的长度；
②：每个位置的字母。
单词的长度很容易，一个计数器就可以搞定了，而每个位置的字母却比较麻烦，因为每个字母都要保存下来，这样会大大增加操作的复杂程度，其实我们可以注意到，一共有26个字母，并且这些字母是连续的，这样我们就可以创建一个长度为26的数组，用这个数组的下标可以和字母形成一一对应的关系，0~25分别对应a~z。

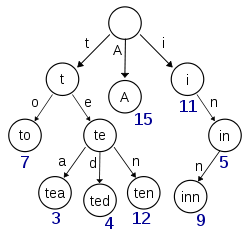
这张图里的树结构，每条边代表一个字母，而一个节点对应的就是该节点的路径，而我们将数组下标和字母组成了一一对应的关系，字母对应的下标是该字母的字符值减去字母a的字符值，例：t对应的下标是’t’-‘a’；
上面的图里，有一点还没有表示清楚，那就是如何判断一个单词是否存在，其实很简单，我们只需要增加一个标记位，对单词的存在与否进行标记就好了。那么来看结构体吧：

typedef struct TrieTree
{
    int isStr;    //标记这个单词是否存在
    struct TrieTree * next[N];//N为26
}Trie;

举个例子吧，比如我已经在树中插入了”liuruiyang”,”liuyufu”,”lijing”这三条记录，由于字母表示边，单词本身表示路径，那么可以肯定，这三条记录的公共边一定有”l”，”i”两个字母，既然我们知道它们的公共边，那么就可以轻松的得到它们的