堆排序

 

堆排序与快速排序，归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。学习堆排序前，先讲解下什么是数据结构中的二叉堆。

堆排序是利用堆的特性对记录序列进行排序的一种排序方法。

即小顶堆：父结点的值小于左右孩子结点的值，大顶堆的相反

假设我们要排序的序列是{50,10,90,30,70,40,80,60,20}

堆排序分为两个步骤：

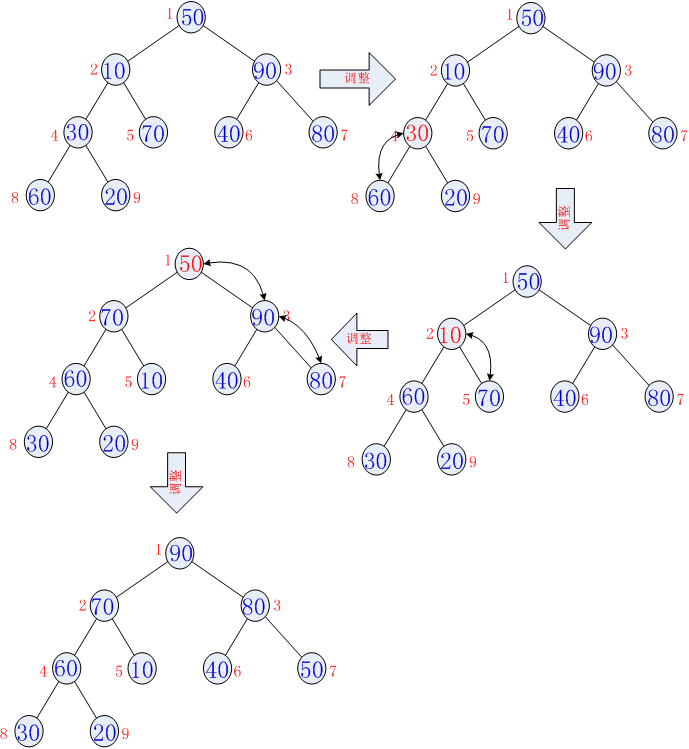
1.构造大顶堆(或者小顶堆)

如图所示：将输入的数组不断调整，使得其构成大顶堆

void HeapAjust(int* arr,int start,int end)
{
	int temp,j;
	temp = arr[start];
	for (j = 2*s;j <= end;j*=2)
	{
		if(j < m && arr[j] < arr[j+1])//左孩子小于右孩子
			j++;
		if(temp >= arr[j])
			break;
		arr[start] = arr[j];
	    start = j;
	}
	arr[start] = temp;
}

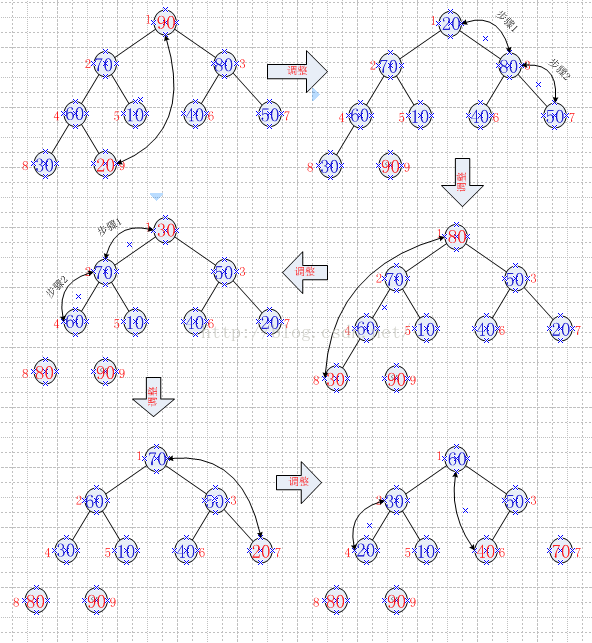
在这里我们使用大顶堆，依次输出元素如下图：

依次类推输出所有元素

程序如下：

void HeapSort(int* arr,int len)
{
	int i;
	for(i = len/2;i>= 0;i--)//构造大顶堆
		HeapAjust(arr,i,len-1);

	for (i = len-1;i > 0;i--)
	{
		swap(arr[0],arr[i]);//取堆顶的记录和当前未经排序子序列的最后一个记录交换
		HeapAjust(arr,1,i-1);
	}
}

这里给出完整代码(仅供参考)：

#include <stdio.h>
#include <stdlib.h>

void swap(int& data1,int &data2)
{
	int temp = data1;
	data1 = data2;
	data2 = temp;
}

//返回i的父结点
int parent(int i)
{
	return (i-1)/2;
}

//返回i的左孩子结点
int leftchild(int i)
{
	return 2*i+1;
}

//返回i的右孩子结点
int rightchild(int i)
{
	return 2*i+2;
}

void MaxHeapify(int *arr,int len,int i)
{
	int lchild = leftchild(i);
	int rchild = rightchild(i);
	int nmax;

	if(lchild < len && arr[lchild] > arr[i])
		nmax = lchild;
	else
		nmax = i;

	if(rchild < len && arr[rchild] > arr[nmax])
		nmax = rchild;

	if (nmax != i)
	{
		swap(arr[nmax],arr[i]);
		MaxHeapify(arr,len,nmax);
	}
}

//堆排序
void HeapSort(int* arr,int len)
{
   for (int i = parent(len - 1);i >= 0;i--)
       MaxHeapify(arr,len,i);
   
   for (int j = len -1;j > 0;j--)
   {
	   swap(arr[j],arr[0]);
	   len--;
	   MaxHeapify(arr,len,0);
   }
}

void print(int* arr,int len)
{
	int i =0;
	while (i < len)
		printf("%d ",arr[i++]);
// 	for (int i = 0;i < len;i++)
// 	{
// 		printf("%d ",arr[i]);
// 	}

}
int main()
{
    int nArr[10] = {4,1,3,2,16,9,10,14,8,7};
    
	printf("排序前：");
    print(nArr, 10);
    HeapSort(nArr, 10);
	printf("\n排序后：");
    print(nArr, 10);
	
	system("pause");
    return 0;
}

复杂度分析：

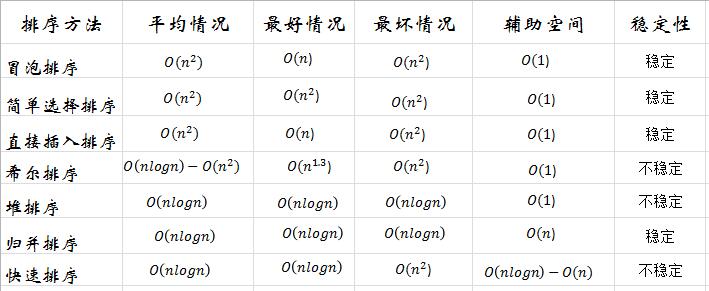
运行时间主要是消耗在初始建堆和重建堆时的反复筛选上，在构建堆的过程中，因为是完全二叉树最下层最右边的非终端结点开始构建，将它与其孩子比较若有必要进行交换，对于每个非终端结点来说，其实最多进行两次比较和呼唤操作，因此整个构建过程的时间复杂度为O(n)，在排序时，第i次取堆顶记录重建时需要使用O(logi)的时间，并需要取 n-1 次堆顶记录，因此重建堆时的时间复杂度为 O(nlogn).因此总体来说堆排序的时间复杂度为  O(nlogn)。由于堆排序对原始记录的排序状态并不敏感，因此他无论是最好、最坏和平均时间复杂度均为  O(nlogn)。这在性能是要超过 冒泡排序、简单选择排序、直接插入排序的 O(n^2) 的时间复杂度。空间复杂度上，他只有一个用来交换的暂存单元，也非常不错。但是由于记录的比较与交换是跳跃式进行，因此堆排序是一种不稳定的排序方法。