1.蛮力算法
核心思路
往往就是直接按照枚举等最基本的问题解决思路去做,其简单实用,适用范围广,但效率往往比较低,规模小或者速度要求低的问题比较适合。
NP问题(文心一言解答)
NP(Non-deterministic Polynomial)问题是计算机科学和数学中的一个重要概念,尤其在理论计算机科学和计算复杂性理论中。为了完全理解NP问题,我们需要先了解几个相关的概念:
- 多项式时间(Polynomial Time):如果一个算法的运行时间可以表示为输入大小n的多项式函数,则称该算法在多项式时间内运行。例如,O(n), O(n^2), O(n^3)等都是多项式时间。
- P问题(Polynomial-time problems):能在多项式时间内找到解决方案的问题被称为P问题。例如,排序、搜索和图的某些基本算法(如广度优先搜索和深度优先搜索)都在多项式时间内运行。
- NP问题(Non-deterministic Polynomial problems):NP问题是这样一类问题,对于给定的一个答案,我们可以在多项式时间内验证这个答案是否正确。但请注意,“非确定性”并不意味着问题实际上不能在确定性机器上解决,而是说存在一个非确定性的算法(即允许猜测或分支的算法)可以在多项式时间内找到解决方案。
一个常见的NP问题的例子是“旅行商问题”(Traveling Salesman Problem, TSP):给定一系列城市和每对城市之间的距离,找出访问每个城市一次并返回原点的最短可能路线。虽然我们可以很容易地验证一个给定的路线是否是最短路线(只需计算总距离并比较即可),但找到这样的路线本身可能是一个复杂的问题,特别是当城市数量增加时。
NP完全问题(NP-complete problems)是NP问题的一个子集,它们具有特殊的性质:如果一个NP完全问题有一个多项式时间的算法,那么所有的NP问题也都有多项式时间的算法。换句话说,NP完全问题是NP问题中最难的一类,因为解决它们需要解决所有NP问题的能力。
NP完全问题有几个关键的特征:
- 它是NP问题:即我们可以在多项式时间内验证一个给定的解是否正确。
- 它具有“多项式时间归约性”:这意味着任何其他的NP问题都可以在多项式时间内转化为这个NP完全问题。
现在,让我们举几个NP完全问题的例子:
-
旅行商问题(Traveling Salesman Problem, TSP):给定一系列城市和每对城市之间的距离,找出访问每个城市一次并返回原点的最短可能路线。
-
顶点覆盖问题(Vertex Cover Problem):给定一个无向图,找出图中的最小顶点集合,使得图中的每一条边都至少与这个集合中的一个顶点相连。
-
子集和问题(Subset Sum Problem):给定一个正整数的集合和一个目标数,判断是否存在集合的一个子集,使得子集内所有数的和等于目标数。
-
哈密顿回路问题(Hamiltonian Cycle Problem):给定一个图,判断是否存在一个回路,它恰好经过图中的每个顶点一次。
-
3-SAT问题(3-Satisfiability Problem):这是一个逻辑问题,给定一组布尔变量和一组子句(每个子句是三个变量的析取式),判断是否存在一种变量的赋值方式,使得所有的子句都为真。
由于NP完全问题的这些性质,它们经常被用作基准问题来评估其他NP问题的难度。如果某个NP问题能够证明是NP完全的,那么我们就可以认为这个问题在多项式时间内没有已知的解决方案,除非P=NP(这是一个未解决的数学问题)。
在实际应用中,由于NP完全问题的难度,我们通常使用近似算法、启发式方法或随机算法来找到“足够好”的解决方案,而不是寻找最优解。
【这里可以发现举出的几个完全NP问题的例子,第一想法都会是用蛮力算法枚举解决,但毫无疑问这些问题哪怕规模不大也会因为问题设置而使得计算量巨大,很好的说明了蛮力算法的特点,简单但效率低】
2.分治算法
核心思路
分而治之,将大问题分解成小问题来处理解决(毫无疑问,看到这里第一想法就是递归,非常典型的分治思路)。但是这样做有个前提条件:求解问题所需的计算时间都与其规模有关,越小的
适用条件
求解过程
应用实例
1.L形骨牌覆盖棋盘(后续补)
题目描述
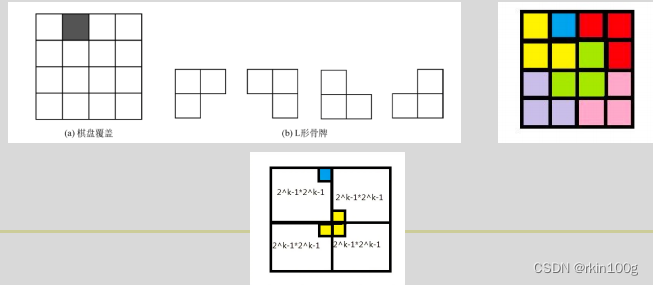
核心思路
每次都将L形骨牌没有的一角放在已经存在一格的方向,这样问题可以继续分解为四个小区域的L形骨牌覆盖棋盘问题,最后就会不断分解到2x2的棋盘里有一个角已经有特殊方格,再放入一个L形骨牌补全的问题,此时再按照将L形骨牌没有的一角放在已经存在一格的方向的思路放L形骨牌就能够填满这个2x2的棋盘,然后不断填满小棋盘就可以了。
2.归并排序、快速排序
3.汉诺塔
4.二分搜索
3.贪心算法
核心思路
适用条件
1. 贪心选择性质
所谓贪心选择性质,是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到 。这是贪心算法可行的第一个基本要素,也是贪心法与动态规划法的主要区别。如活动安排问题、背 包问题、单源最短路径问题等。(每⼀步贪⼼选出来的⼀定是原问题的最优解的⼀部分)
基本步骤
应用实例(后续补)
1.Huffman code
2.最小生成树:Prim算法和Kruskal算法
3. 最短路径:Dijkstra算法
4.作业调度问题

5.找零钱问题
题目描述
6.活动选择

(来自课堂课件)
7.背包问题
①分数背包
②0/1背包问题
4.动态规划算法
核心思路
→备忘录说明
- 备忘录是一种优化技术,用于存储子问题的解,以便在需要时直接查找,而不是重新计算。
- 当再次遇到相同的子问题时,可以直接从备忘录中取出答案,从而避免了不必要的计算。
应用实例
1.斐波那契数列求解问题
很多调用过程都是重复的,所以可以用备忘录把之前已经调用过的数据记录下来。
2.最大连续子序列和问题
不考虑最大的情况下,如果让第i个元素分别作序列的最后一个元素,则可以发现从i=0,到i=n-1,下一次i的这些子序列实在上一个i的这些子序列的基础上都加上一个第i个元素,其最大值也与上一层高度相关,得出了定性关系之后,因为要求最大值,所以我们可以发现,如果上一层各个子序列中最大值是正值,则下一层就在此基础上加上第i个元素,但如果上一层最大值本身就已经是负值,则无需“继承”,直接从第i个元素开始。
例子在相册里
同时我们可以通过mark标记记录从上到下是否继承,最后连续的序列就是最后一个不继承的元素开始,连到下一个不继承的元素(即最后一段跳变的序列,因为每一次跳变都代表着序列大小在变大)
int findmax(int arr[], int n)
{
int maxvalue = -200, temp = 0;
for(int i=0; i<n; i++)
{
if(temp > 0)
{
temp += arr[i];
}
else temp = arr[i];
if(temp > maxvalue) maxvalue = temp;
}
return maxvalue;
}最后来看,它本质仍然是穷举,但是它通过自底向上(从一个元素到全部元素),把大问题拆解成了一层层的小问题,同时最后最大只有与这些小问题的最优解高度相关,而且略过了重复的过程,比如每次到下一层的时候没有全部重新算一遍,而是直接判断加上这一个元素后最大值会怎么变来优化了穷举过程,而且
3.最长公共子序列
最长公共(相对顺序不变不要求完全顺序一样)
首先来推理出最长公共子序列的结构特征尤其是跟上一层下一层(即长度为n和长度为n-1时之间的关系),然后进一步建立两者之间的递归结构(状态转移方程)【要往找长度为n和长度为n-1两者最长公共子序列关系的方向上去想,从而来看是否能够满足最优子结构,把大问题拆解成小问题】



(图片来自课堂课件,截图下来方便后续复习而已)





















 2712
2712











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








