数据结构——树

基本概念

结点的度：结点拥有的子树的数目

树的度：树中结点度的最大值

分支结点（非终端结点）：度不为0

叶子（终端结点）：度为0

结点的层次：从根结点开始定义，为第一层，其孩子为第二层

树的高度/深度：树中结点的最大层次值

有序树：树中结点的各子树看成是从左至右是有次序的（即不可互换），否则为无序树，最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子

森林：m棵互不相交的树的集合，对树中每个结点，其子树的集合即为森林

存储方式：孩子兄弟链式存储（二叉树表示法）

typedef struct CSNode{
    TElemType data;
    struct CSNode *firstchild,*nextsibling;
} CSNode, *CSTree;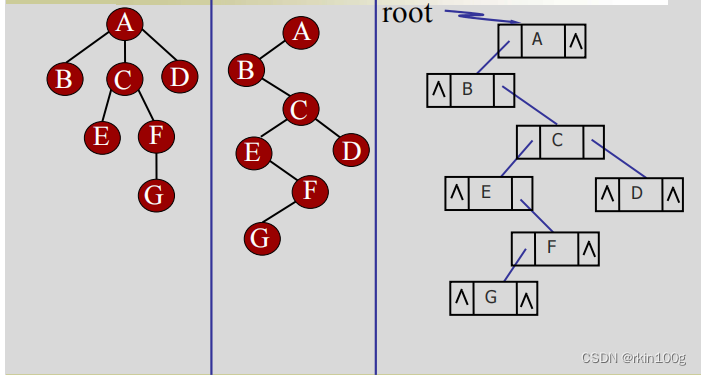

（来自课堂课件）

应用场景

具有层次的集合，如社会组织机构、互联网域名、系统的进程管理

特殊的树：二叉树

基本概念

定义：有一个特定的称之为根的结点，其余结点都分别由两棵互不相交的称之为左子树和右子树的二叉树组成。（非空的情况下）

满二叉树：深度为k且含有2k－1个结点的二叉树为满二叉树

完全二叉树：深度为k，含有n个结点的二叉树，当且仅当每个结点的编号与相应满二叉树结点顺序号从1到n相对应时，则称此二叉树为完全二叉树（？）

特点

可以为空树；

度不大于2，即每个结点至多只有两棵子树；

是有序树，左子树和右子树严格区分且不能随意颠倒

性质

性质1 二叉树第i(i≥1)层上至多有2^i-1个结点。

【至多是q=2的等比数列】

性质2 深度为k(k≥1)的二叉树至多有2^ k －1个结点

【各层结点最多数目之和为2^0 +2^ 1 +2^ 2 +…+2^( k-1)】

性质3 在任意二叉树中，若叶子结点(即度为零的结点)个数为n 0 ， 度为1的结点个数为n1 ，度为2的结点个数为n 2 ，那么n 0 =n 2 +1

（来自课堂课件）

性质4 具有n个结点的完全二叉树深度为[log2 n]+1

【用深度为k和k+1的最大结点树列不等式即可】

存储

1.顺序存储结构

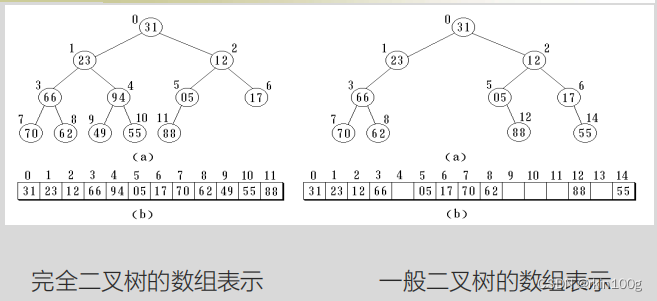
（来自课堂课件）

一般的二叉树必须仿照完全二叉树那样存储，可能会浪费很多存储空间（比如单支树就是一个极端情况），另外就是通过编号来表示各结点之间的连接关系并不直接了当，对程序员理解会造成一定的麻烦。

2.链式存储结构

typedef struct CSNode{
    DataType data;
    struct CSNode *lch,*rch;//用指针记录左子树，右子树
    //struct CSNode *parent;可以根据需要选择是否需要再记录父结点
} CSNode, *CSTree;

遍历

遍历是按某种次序访问树中的结点，且要求每个结点访问一次且仅访问一次。根据访问根结点的顺序分为以下三种遍历方式，都利用递归来实现：

1.先序（先根）遍历

先访问根结点，接着访问左子树，最后访问右子树。

int PreOrder(BiTree T){
    if(T!=NULL){
        printf("%c\n",T->data); /*访问根结点*/
        PreOrder(T->lchild); /*按先根次序遍历左子树*/
        PreOrder(T->rchild); /*按先根次序遍历右子树*/
    }
    return 0;
}

2.中序（中根）遍历

先访问左子树，然后访问根节点，最后访问右子树

3.后序（后根）遍历

先访问左子树，然后访问右子树，最后再访问根结点

遍历复杂度分析

时间复杂度：O(n)

空间复杂度：为二叉树的深度，即O(log2n)

应用案例

1.利用二叉树前序遍历建立二叉树

int CreateBiTree(BiTree* T)
{
    char ch;
    scanf("%c",&ch);//通过输入字符串，每个字符代表结点数据或者空来创建
    if(ch=='@')//代表此处结点为空
    {
        T=NULL;
    }
    else
    {
        T=(BiTNode*)malloc(sizeof(BiTNode));
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
    return 0;
}

2.利用二叉树后序遍历计算二叉树结点个数

int CountBiTree(BiTree T)
{
    if (T == NULL) 
    return 0;
    else
    return (1 + CountBiTree (T->lchild) + CountBiTree (T->rchild));
}

3.利用二叉树后序遍历计算二叉树高度

int DepthBiTree(BiTree &T)
{
    if (T == NULL) 
    return 0;
    else
    return (1 + max( DepthBiTree (T->lchild), DepthBiTree (T->rchild) ));
}

二叉树的应用——霍夫曼树

1.相关概念

结点间路径长度：连接两个结点的路径上的分支数

树的路径长度：各个结点到根结点的路径长度之和

树的带权路径长度：树的各叶结点所带的权值与该结点到根的路径长度的乘积的和

霍夫曼树：带权路径长度最小的二叉树，其表现为权值大的叶结点离根最近

2.构造过程

基本流程

1.根据给定的n个权值{w1,w2,…,wn}构成n棵二叉树（F={T1，T2,…,Tn}），每棵二叉树Ti只有一个带权值为wi的根结点，其左右子树均空。

2. 从F中选取两棵根结点权值最小的树作为左右子树构造一颗新的二叉树，且置新的二叉树的根结点的值为其左右子树上根结点的权值之和。

3. 在F中删除这两颗树，同时将新得到的二叉树加入F中。

4. 重复2、3步骤，直到F只含一颗树为止。这棵树即是霍夫曼树。

代码实现（后序补）

应用

1.编码问题（霍夫曼编码）

给出现频率高的字符编码较短，出现频率低的编码较长