在统计计算中,最大期望(EM,Expectation–Maximization)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Latent Variabl)。最大期望经常用在机器学习和计算机视觉的数据集聚(Data Clustering)领域。最大期望算法经过两个步骤交替进行计算,第一步是计算期望(E),也就是将隐藏变量象能够观测到的一样包含在内从而计算最大似然的期望值;另外一步是最大化(M),也就是最大化在 E 步上找到的最大似然的期望值从而计算参数的最大似然估计。M 步上找到的参数然后用于另外一个 E 步计算,这个过程不断交替进行。
最大期望过程说明
我们用 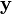 表示能够观察到的不完整的变量值,用
表示能够观察到的不完整的变量值,用  表示无法观察到的变量值,这样
表示无法观察到的变量值,这样  和
和 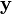 一起组成了完整的数据。
一起组成了完整的数据。 可能是实际测量丢失的数据,也可能是能够简化问题的隐藏变量,如果它的值能够知道的话。例如,在混合模型(Mixture Model)中,如果“产生”样本的混合元素成分已知的话最大似然公式将变得更加便利(参见下面的例子)。
可能是实际测量丢失的数据,也可能是能够简化问题的隐藏变量,如果它的值能够知道的话。例如,在混合模型(Mixture Model)中,如果“产生”样本的混合元素成分已知的话最大似然公式将变得更加便利(参见下面的例子)。
估计无法观测的数据
让  代表矢量 θ:
代表矢量 θ: 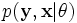 定义的参数的全部数据的概率分布(连续情况下)或者概率集聚函数(离散情况下),那么从这个函数就可以得到全部数据的最大似然值,另外,在给定的观察到的数据条件下未知数据的条件分布可以表示为:
定义的参数的全部数据的概率分布(连续情况下)或者概率集聚函数(离散情况下),那么从这个函数就可以得到全部数据的最大似然值,另外,在给定的观察到的数据条件下未知数据的条件分布可以表示为:







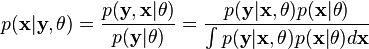














 967
967

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








