期望最大化算法(The EM algorithm)

在上一章中，我们为了解决拟合混合高斯模型的拟合问题已经接触了EM算法。这一章里，我们会进一步扩展EM算法的应用，你会发现它可以用于解决一大类包含隐参数的估计问题。让我们从Jensen不等式开始我们的讨论。

1 Jensen 不等式

设$f$是一个定义域为实数的函数，回忆前面的内容，当$f^{"}(x) \ge 0$是函数$f$就是一个凸函数（下凸）。而当$f$的输入是一个向量时，当它的海森矩阵是一个半正定矩阵时，我们可以说函数$f$是一个严格凸函数。Jensen不等式的表述如下：

定理. 设$f$是一个凸函数，$X$是一个随机变量。那么：

$$E[f(X)] \ge f(EX).$$

不仅如此，若$f$为严格凸时，那么$E[f(X)] = f(EX)$当且仅当$X = E[X]$的概率为1时发生。关于定理的阐述我们可以看看下面这张图片：

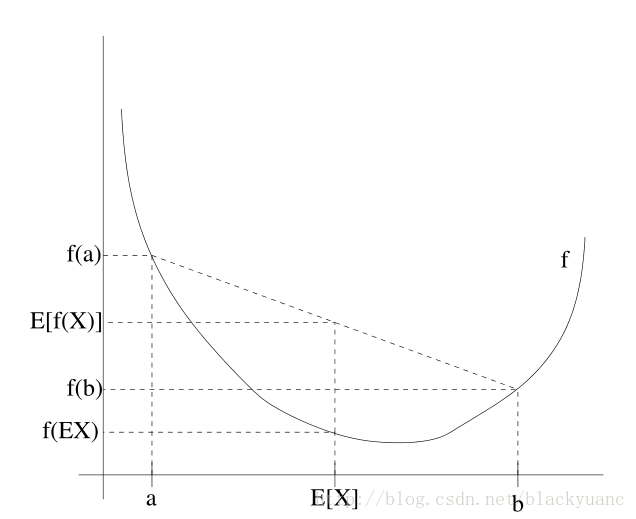
图中凸函数f是实线绘制的曲线，随机变量$X$有50%的概率是a，50%的概率是b，所以$X$的期望是a,b的中点。从这个例子可以看到，只要$f$是凸函数，必有$E[f(X)] \ge f(EX)$。

---

2 EM算法

设某估计问题中有m个独立的样本$\{ x^{(1)}, \ldots, x^{(m)} \}$。我们希望使模型$p(x,z)$的参数和数据拟合，则对数似然函数写成如下形式：

$$\begin{align} \ell(\theta) &= \sum_{i=1}^m \text{log} \ p(x; \theta)\\ &= \sum_{i=1}^m \text{log} \sum_z p(x,z; \theta).\\ \end{align}$$

由于无法直接求解参数$\theta$的极大似然估计，引入隐参数$z^{(i)}$，如果假设隐参数的值已知，那么求解极大似然估计就会变得很容易。

这时求最大似然估计，EM算法是一个行之有效的方法。直接最大化$\ell(\theta)$很困难，但我们的策略是先构造$\ell$的下界(E步骤)，再最优化其下界(M步骤)。过程如下图所示

对每一个$i$，设$z$服从$Q_i$分布($\sum_z Q_i(z) = 1, Q_i(z) \ge 0$)，则下式成立：

$$\begin{align} \sum_i \text{log} p(x^{(i)}; \theta) &= \sum_i \text{log} \sum_{z^{(i)}} p(x^{(i)}, z^{(i)}; \theta) &(1)\\ &= \sum_i \text{log} \sum_{z^{(i)}} Q_i(z^{(i)}) \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} \qquad \qquad &(2)\\ &= \sum_i \text{log} \ \text{E}_{z^{(i)} \sim Q_i} \left[ \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} \right] \\ &\ge \sum_i \text{E}_{z^{(i)} \sim Q_i} \ \left[\text{log} \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} \right]\\ &\ge \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) \ \text{log} \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} &(3)\\ \end{align}$$

因为$f^{"}(x) = -1/x^2 \lt 0$，$f(x) = \text{log}\ x$是一个凹函数。第四步可以根据Jensen不等式求得。

对于任意的分布$Q_i$，方程(3)给出了对数似然函数$\ell(\theta)$的下界。这时$Q_i$分布有很多可能的选择，我们应该如何决定呢？如果我们现在有关于参数$\theta$的假设值，那么很自然下界的选择要和$\theta$相关。
要使下界的选择与$\theta$相关，我们需要推导中使用Jensen不等式的地方变为相等。为此期望值需要是一个常数变量。则有：

$$\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} = c$$

为使常数c不依赖$z^{(i)}$的取值。我们需要$Q_i(z^{(i)})$与$p(x^{(i)}, z^{(i)}; \theta)$成比例。

实际上因为$\sum_z Q_i(z^{(i)}) = 1$，这进一步告诉我们：

$$\begin{align} Q_i(z^{(i)}) &= \frac{p(x^{(i)}, z^{(i)}; \theta)}{\sum_z p(x^{(i)}, z^{(i)}; \theta)} \\ &= \frac{p(x^{(i)}, z^{(i)}; \theta)}{p(x^{(i)}; \theta)} \\ &= p(z^{(i)} | x^{(i)}; \theta) \\ \end{align}$$

我们令$Q_i$为给定$x^{(i)}$与参数$\theta$关于$z^{(i)}$的后验概率。

通过选择$Q_i$，我们求对数似然函数的最大下界，这是E阶段。通过改变参数$\theta$，我们求方程(3)中的最大值。重复执行一上两个步骤就是EM算法：

循环至收敛 {

(E步骤)对每个i，令：

$$Q_i(z^{(i)}) = p(z^{(i)} | x^{(i)}; \theta).$$
(M步骤) 令：
$$\theta := \text{arg}\ \max_\theta \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) \ \text{log} \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}$$

}
EM算法是一个一致收敛的算法。我们在算法描述时说循环至收敛。实际情况下判断收敛的方式一般为，当对数函数的增长小于某一设定值时，我们认为EM算法继续改善的能力已经很小了，即认为其收敛。