译者序
本篇blog实际上是Bob大叔对xreborner的一连串的发贴给于的回复(xreborner在上篇blog中对Bob大叔提出了一系列犀利的维护C++权益的观点)。
正文
我在最近的一篇blog中对比了C++、Java和Ruby的时间消耗,其中一个参与者(xreborner)提交了一个convex hull的凸包算法代码。我花了好久来研究其中的蹊跷,直到把算法绘制于图上,才发现自己是蒙在鼓里了。
xreborner用的算法像是一种Graham Scan算法,它的复杂度呈O(nLogn)级别。实际上,这个算法的时间主要是消耗在其中的快速排序上了。
还有一个算法叫做Jarvis March,也称作giftwrapping算法。它的复杂度呈O(kn)级别,k代表了凸包顶点的数目。
我非常好奇这两个算法哪个会更快些,显然,只有在logn < k的时候,O(nLogn)才会比O(kn)的快。不过也有另一种考量,因为Jarvis March比Graham Scan简单的多,所以我认为在绝大多数情况下,Jarvis March算法都会是个更优的选择,因为只有在凸包顶点数目非常大的情形下Graham算法的效率才会反超。于是我自己编写了Jarvis March算法,并且和xreborner的Graham Scan做了比较,结果如下:
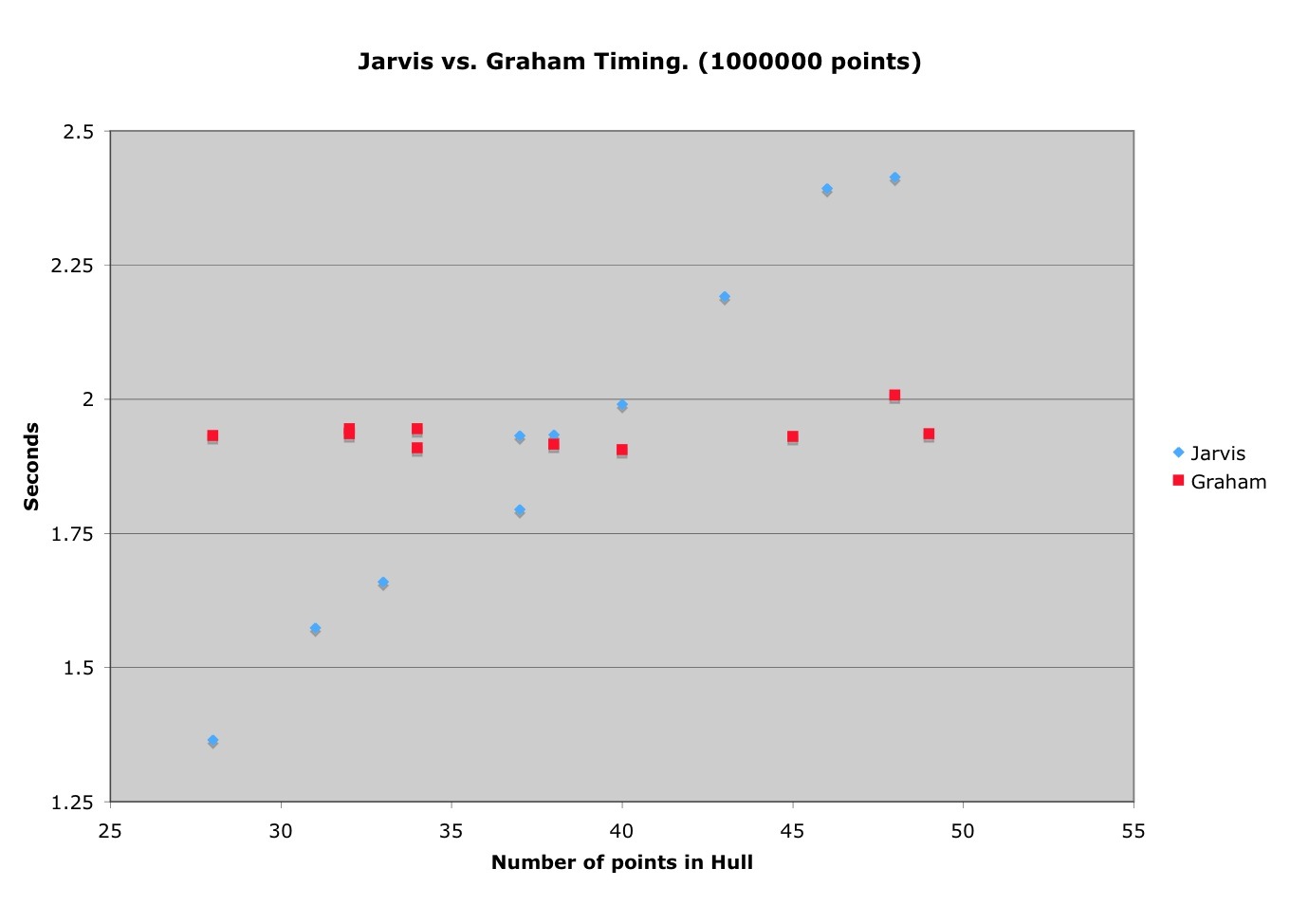 |
是不是很有趣?我构造了1000个随机点并绘制了时间和凸包顶点数量的曲线。交叉点看起来正好位于这些随机的凸包顶点数量的中间位置,而且大概是在37点位!我猜想这是个巧合,不过也够神奇的啊。
噢,作为一个锻炼,看看你们是不是能读懂Jarvis March,也再看看能不能弄明白Graham Scan。
import java.util.*;
public class JarvisMarch {
Points pts;
private Points hullPoints = null;
private List<Double> hy;
private List<Double> hx;
private int startingPoint;
private double currentAngle;
private static final double MAX_ANGLE = 4;
public JarvisMarch(Points pts) {
this.pts = pts;
}
/**
* The Jarvis March, sometimes known as the Gift Wrap Algorithm.
* The next point is the point with the next largest angle.
* <p/>
* Imagine wrapping a string around a set of nails in a board. Tie the string to the leftmost nail
* and hold the string vertical. Now move the string clockwise until you hit the next, then the next, then
* the next. When the string is vertical again, you will have found the hull.
*/
public int calculateHull() {
initializeHull();
startingPoint = getStartingPoint();
currentAngle = 0;
addToHull(startingPoint);
for (int p = getNextPoint(startingPoint); p != startingPoint; p = getNextPoint(p))
addToHull(p);
buildHullPoints();
return hullPoints.x.length;
}
public int getStartingPoint() {
return pts.startingPoint();
}
private int getNextPoint(int p) {
double minAngle = MAX_ANGLE;
int minP = startingPoint;
for (int i = 0; i < pts.x.length; i++) {
if (i != p) {
double thisAngle = relativeAngle(i, p);
if (thisAngle >= currentAngle && thisAngle <= minAngle) {
minP = i;
minAngle = thisAngle;
}
}
}
currentAngle = minAngle;
return minP;
}
private double relativeAngle(int i, int p) {return pseudoAngle(pts.x[i] - pts.x[p], pts.y[i] - pts.y[p]);}
private void initializeHull() {
hx = new LinkedList<Double>();
hy = new LinkedList<Double>();
}
private void buildHullPoints() {
double[] ax = new double[hx.size()];
double[] ay = new double[hy.size()];
int n = 0;
for (Iterator<Double> ix = hx.iterator(); ix.hasNext();)
ax[n++] = ix.next();
n = 0;
for (Iterator<Double> iy = hy.iterator(); iy.hasNext();)
ay[n++] = iy.next();
hullPoints = new Points(ax, ay);
}
private void addToHull(int p) {
hx.add(pts.x[p]);
hy.add(pts.y[p]);
}
/**
* The PseudoAngle is a number that increases as the angle from vertical increases.
* The current implementation has the maximum pseudo angle < 4. The pseudo angle for each quadrant is 1.
* The algorithm is very simple. It just finds where the angle intesects a square and measures the
* perimeter of the square at that point. The math is in my Sept '06 notebook. UncleBob.
*/
public static double pseudoAngle(double dx, double dy) {
if (dx >= 0 && dy >= 0)
return quadrantOnePseudoAngle(dx, dy);
if (dx >= 0 && dy < 0)
return 1 + quadrantOnePseudoAngle(Math.abs(dy), dx);
if (dx < 0 && dy < 0)
return 2 + quadrantOnePseudoAngle(Math.abs(dx), Math.abs(dy));
if (dx < 0 && dy >= 0)
return 3 + quadrantOnePseudoAngle(dy, Math.abs(dx));
throw new Error("Impossible");
}
public static double quadrantOnePseudoAngle(double dx, double dy) {
return dx / (dy + dx);
}
public Points getHullPoints() {
return hullPoints;
}
public static class Points {
public double x[];
public double y[];
public Points(double[] x, double[] y) {
this.x = x;
this.y = y;
}
// The starting point is the point with the lowest X
// With ties going to the lowest Y. This guarantees
// that the next point over is clockwise.
int startingPoint() {
double minY = y[0];
double minX = x[0];
int iMin = 0;
for (int i = 1; i < x.length; i++) {
if (x[i] < minX) {
minX = x[i];
iMin = i;
} else if (minX == x[i] && y[i] < minY) {
minY = y[i];
iMin = i;
}
}
return iMin;
}
}
}
(原文链接网址:http://www.butunclebob.com/ArticleS.UncleBob.ConvexHullTiming; Robert C. Martin的英文blog网址: http://www.butunclebob.com/ArticleS.UncleBob)
作者简介:Robert C. Martin是Object Mentor公司总裁,面向对象设计、模式、UML、敏捷方法学和极限编程领域内的资深顾问。他不仅是Jolt获奖图书《敏捷软件开发:原则、模式与实践》(中文版)(《敏捷软件开发》(英文影印版))的作者,还是畅销书Designing Object-Oriented C++ Applications Using the Booch Method的作者。Martin是Pattern Languages of Program Design 3和More C++ Gems的主编,并与James Newkirk合著了XP in Practice。他是国际程序员大会上著名的发言人,并在C++ Report杂志担任过4年的编辑。
























 238
238











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








