ZCMU1934: ly的二叉树（卡特兰数算法+快速幂+逆元的求法）

最新推荐文章于 2024-03-24 23:00:01 发布

rnzhiw

最新推荐文章于 2024-03-24 23:00:01 发布

阅读量766

点赞数

分类专栏： acm 文章标签： acm c 快速幂求逆元卡特兰数算法

本文链接：https://blog.csdn.net/rnzhiw/article/details/81166964

版权

acm 专栏收录该内容

54 篇文章 1 订阅

订阅专栏

ly的二叉树：

Description

某一天，ly正在上数据结构课。老师在讲台上面讲着二叉树，ly在下面发着呆。
突然ly想到一个问题：对于一棵n个无编号节点的有根二叉树，有多少种形态呐？你能告诉她吗？

Input

多组输入，处理到文件结束
每一组输入一行，一个正整数n(1≤n≤1000000),意义如题目所述。

Output

每组数据输出一行，包含一个正整数表示答案，由于数字可能非常大，你只需要把最后的结果对1000000007取模即可。

Sample Input

Sample Output

在做这道关于有n个结点的二叉树的多种形态的问题的时候，这个曾经也是阿里的面试题，经过分析这道题后输入的正整数可能会非常大，所以依靠单纯的卡特兰数算法可能会超时，先讲一下卡特兰数算法吧：

卡特兰数算法：

在维基百科上显示的资料：

卡塔兰数是组合数学中一个常出现在各种计数问题中出现的数列。

卡塔兰数的一般项公式为 $C_n = \frac{1}{n+1}{2n \choose n} = \frac{(2n)!}{(n+1)!n!}$ 另类递归式： h(n)=((4*n-2)/(n+1))*h(n-1);

这个其实非常好用，我总结了他的几个应用：

1.Cn表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串，且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:

XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY

2.将上例的X换成左括号，Y换成右括号，Cn表示所有包含n组括号的合法运算式的个数:

((())) ()(()) ()()() (())() (()())

3.Cn表示所有在n × n格点中不越过对角线的单调路径的个数。一个单调路径从格点左下角出发，在格点右上角结束，每一步均为向上或向右。计算这种路径的个数等价于计算Dyck word的个数： X代表“向右”，Y代表“向上”。下图为n = 4的情况：

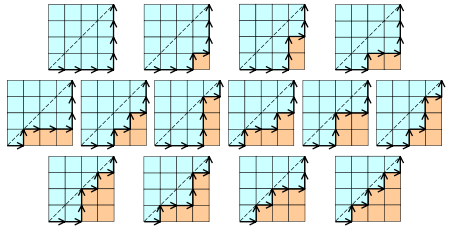
4.Cn表示通过连结顶点而将n + 2边的凸多边形分成三角形的方法个数。下图中为n = 4的情况：

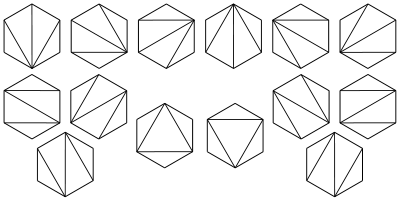
5.出栈次序问题。
一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
　　类似：
　　(1)有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)
　　(2)在圆上选择2n个点,将这些点成对连接起来，使得所得到的n条线段不相交的方法数。
3.将多边行划分为三角形问题。

　　将一个凸多边形区域分成三角形区域的方法数?
　　类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她
　　从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？
　　类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?

6.给顶节点组成二叉树的问题。

　　给定N个节点，能构成多少种形状不同的二叉树？
　　(一定是二叉树!
　　先去一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) + + h(n-1)h(0)=h(n))
　　（能构成h（N）个）

快速求幂：

转自：https://www.cnblogs.com/lca1826/p/6748372.html

快速幂这个东西比较好理解，但实现起来到不老好办，记了几次老是忘，今天把它系统的总结一下防止忘记。

首先，快速幂的目的就是做到快速求幂，假设我们要求a^b,按照朴素算法就是把a连乘b次，这样一来时间复杂度是O(b)也即是O(n)级别，快速幂能做到O(logn)，快了好多好多。它的原理如下：

　　假设我们要求a^b，那么其实b是可以拆成二进制的，该二进制数第i位的权为2^(i-1)，例如当b==11时，a^11=a^(2^0+2^1+2^3)

　　11的二进制是1011，11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1，因此，我们将a¹¹转化为算 a^(2^0)*a^(2^1)*a^(2^3) ，看出来快的多了吧原来算11次，现在算三次，但是这三项貌似不好求的样子....不急，下面会有详细解释。

因为十进制数b可以用二进制表示为： $b=b_{0}*2^{^{0}}+b_{1}*2^{^{1}}+b_{2}*2^{^{2}}+b_{3}*2^{^{3}}+...+b_{n}*2^{^{n}}$ 其中bn表示b的二进制形式中的第n位。（其实就是个二进制转十进制公式）

故a的b次方可以表示为 $a^{b}=a^{b_{0}*2^{^{0}}+b_{1}*2^{^{1}}+b_{2}*2^{^{2}}+b_{3}*2^{^{3}}+...+b_{n}*2^{^{n}}}=a^{b_{0}*2^{0}}*a^{b_{1}*2^{1}}*a^{b_{2}*2^{2}}*a^{b_{4}*2^{4}}*...*a^{b_{n}*2^{n}}$

这就是快速幂算法的理论公式了。

　　由于是二进制，很自然地想到用位运算这个强大的工具： & 和 >> ，&运算通常用于二进制取位操作，例如一个数 & 1 的结果就是取二进制的最末位。还可以判断奇偶x&1==0为偶，x&1==1为奇。>>运算比较单纯,二进制去掉最后一位，不多说了，先放代码再解释。

long long int quickpow(long long int a,long long int b)//快速幂运算 
{
	a=a%mod;//取模 
	long long int res=1;//res用于记录结果 
	for(;b;b>>=1)
	{
		if(b&1)//如果二进制末尾是奇数，则执行下面的操作 
		{
			res=(res*a)%mod;
		}
		a=(a*a)%mod;//每次进行记录，用于下一个循环的累乘 
	}
	return res;//求好的幂 
}

代码很短，死记也可行，但最好还是理解一下吧，其实也很好理解，以b==11为例，b=>1011,二进制从右向左算，但乘出来的顺序是 a^(2^0) * a^(2^1) * a^(2^3)，是从左向右的。我们不断的让base*=base目的即是累乘，以便随时对ans做出贡献。

　　其中要理解base*=base这一步，看：：：base*base==base^2,下一步再乘，就是base^2*base^2==base^4,然后同理 base^4 * base4 = base^8 ,,,,, see?是不是做到了base-->base^2-->base^4-->base^8-->base^16-->base^32.......指数正是 2^i 啊，再看上面的例子，a¹¹ = a^(2^0) * a^(2^1) * a^(2^3)，这三项是不是完美解决了，，嗯，快速幂就是这样。

　　顺便啰嗦一句，由于指数函数是爆炸增长的函数，所以很有可能会爆掉int的范围，根据题意决定是用 long long啊还是unsigned int啊还是mod某个数啊自己看着办。

　　还有，矩阵快速幂的求法唯一的区别就是*换成矩阵中的乘法，写个函数代换嘛，思想一毛一样。

求逆元：

可将对商取模转换为对被除数和其除数关于1000000007的逆元，即：

(a / b) % p = (a % p * inv(b) % p) % p

将除数用其逆元替换，将除法转为乘法可得出不爆表的结果。

求逆元的公式为：

a关于b的逆元等于a^(b-2)，（一般都是在普通求逆元会超范围的情况下会引入快速幂算法）。

下面代码片段：

long long int inv(long long int a,long long int b)//求逆元 
{
	return quickpow(a,b-2);
}

接下来展示该题的代码：

/**********************
此题求有n个结点的树有多少种的形态
（大数取模求逆元） 
1.运用卡特兰数的递归算法
2.运用快速幂求逆元 
**********************/
#include<bits/stdc++.h>
using namespace std;
#define mod 1000000007//在输出大数的时候就要取模 
int ans[1000000];//定义一个输出数组 
long long int quickpow(long long int a,long long int b)//快速幂运算 
{
	a=a%mod;//取模 
	long long int res=1;//res用于记录结果 
	for(;b;b>>=1)
	{
		if(b&1)//如果二进制末尾是奇数，则执行下面的操作 
		{
			res=(res*a)%mod;
		}
		a=(a*a)%mod;//每次进行记录，用于下一个循环的累乘 
	}
	return res;//求好的幂 
}
long long int inv(long long int a,long long int b)//求逆元 
{
	return quickpow(a,b-2);
}	
int main()
{
	long long int n, i;//n是输入的数 
	ans[0] = 0; ans[1] = 1;//ans数组进行统计 
	for (i = 2; i <= 1000000; i++)
	{
		ans[i]=ans[i-1] * (4 * i-2) % mod*inv(i+1, mod) % mod;//卡特兰数的递归表示 
	}
	while(scanf("%lld",&n)!=EOF)//输入n个结点，直接输出二叉树的多种形态 
	{
		printf("%d\n", ans[n]);
	}
	return 0;
}

如有错误，请帮忙指出，谢谢！

rnzhiw

关注

0
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
ZCMU1934: ly的二叉树（卡特兰数算法+快速幂+逆元的求法）

ly的二叉树：Description某一天，ly正在上数据结构课。老师在讲台上面讲着二叉树，ly在下面发着呆。突然ly想到一个问题：对于一棵n个无编号节点的有根二叉树，有多少种形态呐？你能告诉她吗？Input多组输入，处理到文件结束每一组输入一行，一个正整数n(1≤n≤1000000),意义如题目所述。Output每组数据输出一行，包含一个正整数表示答案，由于数字可能非...
复制链接

扫一扫