Zernike矩

http://blog.csdn.net/wrj19860202/article/details/6334275

Zernike在1934年引入了一組定義在單位圓 上的復值函數集{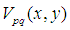 }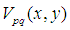，{ }具有完備性和正交性，使得它可以表示定義在單位圓盤內的任何平方可積函數。其定義為：

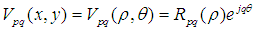
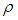 表示原點到點 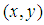的矢量長度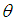； 表示矢量 與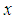 軸逆時針方向的夾角。

 是實值徑向多項式：

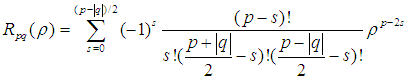
稱為Zernike多項式。

Zernike多項式滿足正交性：

其中

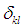 為克羅內克符號，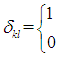 

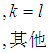
 是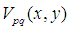 的共軛多項式。

由於Zernike多項式的正交完備性，所以在單位圓內的任何圖像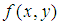 都可以唯一的用下面式子來展開：

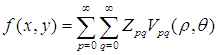
式子中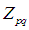 就是Zernike矩，其定義為：

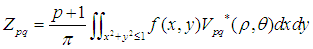
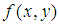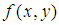注意式子中 和 采用的是不同的坐標系（ 采用直角坐標，而 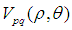采用的極坐標系，在計算的時候要進行坐標轉換）

對於離散的數字圖像，可將積分形式改為累加形式：

 

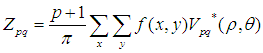
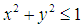
我們在計算一副圖像的Zernike矩時，必須將圖像的中心移到坐標的原點，將圖像的像素點映射到單位圓內，由於Zernike矩具有旋轉不變性，我們可以將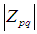 作為圖像的不變特征，其中圖像的低頻特征有p值小的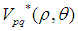提取，高頻特征由p值高的 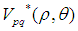提取。從上面可以看出，Zernike矩可以構造任意高階矩。

由於Zernike矩只具有旋轉不變性，不具有平移和尺度不變性，所以要提前對圖像進行歸一化，我們采用標准矩的方法來歸一化一副圖像，標准矩定義為：

 ，

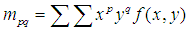由標准矩我們可以得到圖像的"重心"，

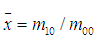
我們將圖像的"重心"移動到單位圓的圓心（即坐標的原點），便解決了平移問題。

我們知道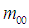 表征了圖像的"面積"，歸一圖像的尺度無非就是把他們的大小變為一致的，（這裡的大小指的是圖像目標物的大小，不是整幅圖像的大小，"面積"也是目標物的"面積"）。

所以，對圖像進行變換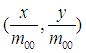 就可以達到圖像尺寸一致的目的。

綜合上面結果，對圖像進行 變換，最終圖像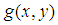 的Zernike矩就是平移，尺寸和旋轉不變的。

<![endif]-->

Zernike 不變矩相比 Hu 不變矩識別效果會好一些，因為他描述了圖像更多的細節內容，特別是高階矩，但是由於Zernike 不變矩計算時間比較長，所以出現了很多快速的算法，大家可以 google 一下。

用 Zernike 不變矩來識別手勢輪廓，識別率大約在 40%~50% 之間，跟 Hu 不變矩一樣， Zernike 不變矩一般用來描述目標物形狀佔優勢的圖像，不適合用來描述紋理豐富的圖像，對於紋理圖像，識別率一般在 20%~30% 左右，很不佔優勢。