打卡信奥刷题（2203）用C++实现信奥 P12717 [Algo Beat Contest 002 D] Distance of Trip

Loge编程生活

于 2025-10-11 14:45:55 发布

阅读量550

点赞数 9

CC 4.0 BY-SA版权

分类专栏： C++ 文章标签： c++ 开发语言算法青少年编程数据结构

本文链接：https://blog.csdn.net/rogeliu/article/details/153030667

C++ 专栏收录该内容

2230 篇文章

订阅专栏

P12717 [Algo Beat Contest 002 D] Distance of Trip

题目背景

Problem	Score	Idea	Std	Data	Check	Solution
$\text{D - Distance of Trip}$	$400$	zhoumurui	zhoumurui	joe_zxq	joe_zxq	Link by zhoumurui

题目描述

在和小伙伴们一起玩耍了几天后，Cirno 开始觉得没日没夜地玩冻青蛙的游戏对她而言已经有些无聊了。她悄无声息地离开了雾之湖，她要出去走走。

第二天早上，Cirno 发现自己身处于草木繁茂的森林中，她不知道她是怎么走到这个地方来的，但好在她还随身携带了指南针。她决定一直往一个方向走，这样一定能够离开森林。

接下来的 $T$ 秒，每一秒 Cirno 会从以下 $3$ 个选项中等概率随机选择一项：

向东移动 $1$ 米。
向南移动 $1$ 米。
先向东移动 $1$ 米，然后向南移动 $1$ 米。

现在告诉你 $T$ ，请你计算 Cirno 在 $T$ 秒内的位移大小的期望值。

Cirno 一段时间内的位移大小定义为这段时间结束前 Cirno 的位置和结束后 Cirno 的位置的直线距离。

输入格式

输入一行一个整数 $T$ ，表示 Cirno 移动的时间。

输出格式

输出一行一个实数，表示 $T$ 秒内移动的距离的期望值。

本题使用 SPJ，你的代码获得一个测试点的分数当且仅当你的代码对于该测试点的输入数据输出的答案与该测试点的输出数据的差不大于 $10^{-6}$ 。

输入输出样例 #1

输入 #1

输出 #1

2.06679179

说明/提示

【样例解释 #1】

有以下 $9$ 种可能：

Cirno 在第一秒向东移动了 $1$ 米，在第二秒向东移动了 $1$ 米。Cirno 移动的距离是 $2$ 米。
Cirno 在第一秒向东移动了 $1$ 米，在第二秒向南移动了 $1$ 米。Cirno 移动的距离是 $\sqrt2$ 米。
Cirno 在第一秒向东移动了 $1$ 米，在第二秒向东移动了 $1$ 米又向南移动 $1$ 米。Cirno 移动的距离是 $\sqrt5$ 米。
Cirno 在第一秒向南移动了 $1$ 米，在第二秒向东移动了 $1$ 米。Cirno 移动的距离是 $\sqrt2$ 米。
Cirno 在第一秒向南移动了 $1$ 米，在第二秒向南移动了 $1$ 米。Cirno 移动的距离是 $2$ 米。
Cirno 在第一秒向南移动了 $1$ 米，在第二秒向东移动了 $1$ 米又向南移动 $1$ 米。Cirno 移动的距离是 $\sqrt5$ 米。
Cirno 在第一秒向东移动了 $1$ 米又向南移动 $1$ 米，在第二秒向东移动了 $1$ 米。Cirno 移动的距离是 $\sqrt5$ 米。
Cirno 在第一秒向东移动了 $1$ 米又向南移动 $1$ 米，在第二秒向南移动了 $1$ 米。Cirno 移动的距离是 $\sqrt5$ 米。
Cirno 在第一秒向东移动了 $1$ 米又向南移动 $1$ 米，在第二秒向东移动了 $1$ 米又向南移动 $1$ 米。Cirno 移动的距离是 $2\sqrt2$ 米。

以上 $9$ 种可能发生的概率均为 $1/9$ ，因此 Cirno 移动的距离的期望值为 $\displaystyle \frac{1}{9} \times (2+\sqrt2+\sqrt5+\sqrt2+2+\sqrt5+\sqrt5+\sqrt5+2\sqrt2) = \frac{4+4\sqrt2+4\sqrt5}{9}$ ，约等于 $2.06679179$ 。

【数据范围】

$\le T \le 200$ 。

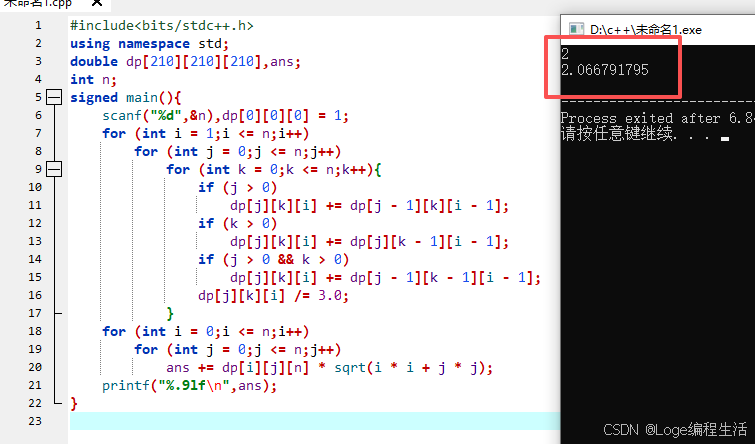
C++实现

#include<bits/stdc++.h>
using namespace std;
double dp[210][210][210],ans;
int n;
signed main(){
	scanf("%d",&n),dp[0][0][0] = 1;
	for (int i = 1;i <= n;i++)
		for (int j = 0;j <= n;j++)
			for (int k = 0;k <= n;k++){
				if (j > 0) 
					dp[j][k][i] += dp[j - 1][k][i - 1];
				if (k > 0) 
					dp[j][k][i] += dp[j][k - 1][i - 1];
				if (j > 0 && k > 0) 
					dp[j][k][i] += dp[j - 1][k - 1][i - 1];
				dp[j][k][i] /= 3.0;
			}
	for (int i = 0;i <= n;i++)
		for (int j = 0;j <= n;j++) 
			ans += dp[i][j][n] * sqrt(i * i + j * j);
	printf("%.9lf\n",ans);
}