[图解]建模相关的基础知识-09

1
00:00:01,350 --> 00:00:03,780
首先，我们来看一下什么叫关系

2
00:00:05,370 --> 00:00:08,990
这个关系跟下面说的这些关系

3
00:00:09,000 --> 00:00:10,390
它不是一个东西

4
00:00:11,110 --> 00:00:14,950
比如说，我们UML类图上，类有关系

5
00:00:15,740 --> 00:00:19,080
还有，用例跟用例有关系等等

6
00:00:21,650 --> 00:00:25,760
里面说的关系就是图上那根线

7
00:00:26,890 --> 00:00:30,610
图上的连接符，两个结点

8
00:00:32,450 --> 00:00:34,850
不管这结点是类还是用例还是什么

9
00:00:35,100 --> 00:00:37,370
还是一个执行者一个用例之类的

10
00:00:37,790 --> 00:00:39,460
中间有根线

11
00:00:39,820 --> 00:00:41,190
线有时还带一个箭头

12
00:00:42,210 --> 00:00:43,250
这个叫关系

13
00:00:46,250 --> 00:00:51,800
但是这里说的关系跟这个不是一个东西

14
00:00:53,550 --> 00:00:55,550
跟UML的类关系

15
00:00:56,200 --> 00:00:58,070
用例关系不是一个意思

16
00:00:58,520 --> 00:01:00,080
也跟实体关系图

17
00:01:00,090 --> 00:01:01,490
那个关系

18
00:01:01,500 --> 00:01:02,610
不是一个

19
00:01:02,620 --> 00:01:05,550
实体关系图的关系跟我们类图上面的类关系

20
00:01:05,560 --> 00:01:06,790
是差不多的

21
00:01:10,250 --> 00:01:11,160
关系是什么

22
00:01:11,680 --> 00:01:15,280
我们前面讲了集合

23
00:01:15,600 --> 00:01:21,180
然后集合A乘B，就是笛卡尔积

24
00:01:22,960 --> 00:01:25,790
关系就是从A×B里面

25
00:01:26,840 --> 00:01:27,840
挑出一些

26
00:01:28,490 --> 00:01:29,910
挑出一些来

27
00:01:31,990 --> 00:01:35,350
挑出一些AB的对应关系来

28
00:01:37,160 --> 00:01:39,830
这样的子集，就叫一个关系

29
00:01:39,840 --> 00:01:47,100
也就是说，关系里面的任何一个元素

30
00:01:47,720 --> 00:01:54,040
它都属于A乘B这个里面的元素

31
00:01:54,860 --> 00:02:00,370
比如说，刚才我们讲集合

32
00:02:00,380 --> 00:02:04,250
集合A是xyz，集合B，12 

33
00:02:04,980 --> 00:02:07,290
如果笛卡尔积应该有6个

34
00:02:08,130 --> 00:02:11,030
3×2=6个，x1

35
00:02:12,360 --> 00:02:14,830
应该是这样，X→1，X→2

36
00:02:15,530 --> 00:02:16,730
Y→1，Y→2

37
00:02:17,260 --> 00:02:17,730

38
00:02:18,250 --> 00:02:21,840
然后Z→1、Z→2这样的，应该有6个

39
00:02:25,220 --> 00:02:26,730
这6个是不是关系，是的

40
00:02:27,910 --> 00:02:31,780
但是只要你是在从这6个里面

41
00:02:31,790 --> 00:02:35,580
挑出任何1个或几个来

42
00:02:37,690 --> 00:02:43,160
都算是A到B的关系

43
00:02:44,750 --> 00:02:50,150
比如说，这里面就挑了4个

44
00:02:50,960 --> 00:02:53,340
1个2个3个4个

45
00:02:53,990 --> 00:02:59,650
这就是其中的1个关系

46
00:03:07,430 --> 00:03:09,870
或者说，R是从集合A到

47
00:03:09,880 --> 00:03:12,500
集合B的一种二元关系

48
00:03:15,450 --> 00:03:19,360
你看，上面这个，它是A乘B的子集

49
00:03:19,970 --> 00:03:23,300
我们前面讲了幂集，实际上就等价于什么

50
00:03:24,740 --> 00:03:28,840
R是A乘B的幂集的元素

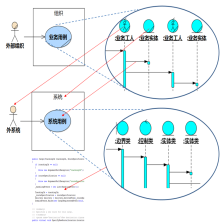
51
00:03:29,580 --> 00:03:30,940
我是你的子集

52
00:03:30,950 --> 00:03:35,380
我是你的幂集的元素，一样的

53
00:03:39,750 --> 00:03:42,090
这是关系的概念

54
00:03:47,500 --> 00:03:55,290
我们来看，这个映射

55
00:03:55,380 --> 00:04:03,040
我们看另外一种更特别的关系

56
00:04:03,290 --> 00:04:04,760
比关系要特别一点的

57
00:04:06,680 --> 00:04:11,480
没有两个元素有相同第1坐标的二元关系

58
00:04:15,460 --> 00:04:22,880
就是说，左边这个第1坐标一旦定了

59
00:04:23,240 --> 00:04:25,810
右边只能有一个

60
00:04:27,300 --> 00:04:29,800
所以，像这个就不是

61
00:04:29,810 --> 00:04:33,720
你看，X这个地方它有两个对应值

62
00:04:34,780 --> 00:04:41,360
一个1个2，也就是说，集合有X，1

63
00:04:41,370 --> 00:04:41,760
X，2

64
00:04:41,770 --> 00:04:44,580
这两个是同一个第1坐标的

65
00:04:45,860 --> 00:04:46,270

66
00:04:48,390 --> 00:04:49,570
第1坐标是一样的

67
00:04:51,230 --> 00:04:56,260
所以这个就不叫函数

68
00:04:56,270 --> 00:04:59,850
函数就是没有两个元素有相同

69
00:04:59,860 --> 00:05:01,170
第1坐标的二元关系

70
00:05:01,790 --> 00:05:02,980
所以这个不是函数

71
00:05:03,440 --> 00:05:05,590
什么才是，把其中一个删掉

72
00:05:06,200 --> 00:05:08,760
比如说，这里，不要这个了

73
00:05:11,060 --> 00:05:12,260
这就行，对不对

74
00:05:12,270 --> 00:05:14,300
把X，2这个删掉

75
00:05:15,190 --> 00:05:16,020
这个就可以

76
00:05:24,870 --> 00:05:28,450
那么如果在图上来表达，意思是什么

77
00:05:28,460 --> 00:05:31,380
就是集合上的每个元素

78
00:05:32,950 --> 00:05:39,060
都恰好有一条出发的箭头

79
00:05:39,070 --> 00:05:44,930
有而且恰好有一条，必须要有

80
00:05:45,140 --> 00:05:47,490
因为你要是没有，意味着什么

81
00:05:48,340 --> 00:05:50,130
给定你一个这个值

82
00:05:50,910 --> 00:05:53,240
你这边找不到对应的

83
00:05:53,250 --> 00:05:56,950
问你，当这个是Z的时候，这边是多少

84
00:05:57,280 --> 00:05:57,910
没有

85
00:05:58,300 --> 00:05:58,610

86
00:06:02,460 --> 00:06:04,250
显然那就不符合我们刚才讲的

87
00:06:04,260 --> 00:06:06,250
从这里面挑的都有

88
00:06:06,510 --> 00:06:07,980
那就不是从这里面挑了

89
00:06:09,190 --> 00:06:11,710
从笛卡尔积里面挑了

90
00:06:12,250 --> 00:06:14,170
肯定有

91
00:06:14,490 --> 00:06:16,080
而且恰好只有一条

92
00:06:18,920 --> 00:06:23,340
那么二元关系就可以叫做该集合上的函数

93
00:06:23,550 --> 00:06:25,460
比如说，这个就可以叫集合A上

94
00:06:25,710 --> 00:06:30,670
如果把这个删掉，抹掉的话

95
00:06:31,120 --> 00:06:33,760
那么这个就可以叫集合A上的一个函数

96
00:06:34,050 --> 00:06:38,760
函数就是一个特殊的关系

97
00:06:41,950 --> 00:06:43,950
那么这个函数，后面我们还会看到

98
00:06:44,120 --> 00:06:46,950
很多地方还会再出现的

99
00:06:46,960 --> 00:06:49,310
包括我们讲的什么函数依赖

100
00:06:50,500 --> 00:06:53,460
x→y，意味着什么

101
00:06:54,080 --> 00:06:57,020
x定了

102
00:06:57,030 --> 00:06:58,020
y就定了

103
00:06:59,550 --> 00:07:05,630
x决定y，y依赖于

104
00:07:05,640 --> 00:07:10,410
依赖于x，或者x决定了y 

105
00:07:10,420 --> 00:07:13,090
函数决定了y，一会还会再说到

106
00:07:17,820 --> 00:07:22,790
在说我们怎样建模的规范化的时候

107
00:07:23,000 --> 00:07:24,350
还会再说到这个问题

108
00:07:26,540 --> 00:07:31,240
或者说，形式上定义得严格一点

109
00:07:31,250 --> 00:07:33,940
就是这个，F是A上的函数

110
00:07:34,680 --> 00:07:36,780
当且仅当

111
00:07:38,220 --> 00:07:44,470
F是这个A乘B幂集的元素

112
00:07:44,480 --> 00:07:46,950
就是F是A乘B的子集了

113
00:07:46,960 --> 00:07:49,870
意思这个就是关系了

114
00:07:50,350 --> 00:07:54,050
这就是关系

115
00:07:55,700 --> 00:07:56,970
这是第一个条件

116
00:07:57,220 --> 00:07:58,810
下面就是后面的条件

117
00:07:59,870 --> 00:08:01,690
这是关系

118
00:08:02,590 --> 00:08:09,310
任意的p1、p2

119
00:08:10,450 --> 00:08:12,660
F里面挑两个p1p2

120
00:08:13,610 --> 00:08:15,090
如果p1不等于p2

121
00:08:16,130 --> 00:08:16,770
意味着什么

122
00:08:17,640 --> 00:08:19,700
π1(p1)不等于π1（p2），也就是说

123
00:08:21,720 --> 00:08:24,260
两根不同的线的话

124
00:08:25,790 --> 00:08:30,200
它不应该有同样的第1坐标

125
00:08:30,210 --> 00:08:32,520

126
00:08:38,640 --> 00:08:40,110
如果p1、p2不相同

127
00:08:40,370 --> 00:08:42,280
第1坐标应该不同

128
00:08:43,700 --> 00:08:46,070
如果相同，那就是刚才那个了

129
00:08:46,790 --> 00:08:52,230
X，1、X，2，就出现这个了

130
00:08:52,240 --> 00:08:53,470
那就不是函数了

131
00:08:54,440 --> 00:08:58,020
那么这个时候，给你个x的值

132
00:08:58,030 --> 00:08:59,220
你到底值是多少

133
00:08:59,230 --> 00:09:01,000
是1是2

134
00:09:01,010 --> 00:09:01,760
那就不定了

135
00:09:04,660 --> 00:09:06,300
这是第一个条件

136
00:09:06,310 --> 00:09:07,420
第二个条件

137
00:09:07,430 --> 00:09:08,740
这是与

138
00:09:09,080 --> 00:09:11,450
都是与，同时成立的

139
00:09:12,050 --> 00:09:14,730
第三个条件，第1坐标

140
00:09:19,650 --> 00:09:24,260
π1(p)，第1坐标

141
00:09:24,270 --> 00:09:31,530
它是组成了A这个集合

142
00:09:31,540 --> 00:09:35,120
也就是说，这个第1坐标是在A里面的

143
00:09:36,060 --> 00:09:37,370
第1坐标的集合

144
00:09:37,380 --> 00:09:40,460
合并起来

145
00:09:40,470 --> 00:09:42,670
刚好就是A，第1坐标集合

146
00:09:42,680 --> 00:09:44,600
就是A，也就是说

147
00:09:44,610 --> 00:09:46,160
A的每个元素

148
00:09:46,170 --> 00:09:48,670
都必须作为第1坐标出现

149
00:09:48,680 --> 00:09:56,330
这样来通过比较形式化的方式来表达它

150
00:10:02,940 --> 00:10:07,610
我们看，下面哪些是函数

151
00:10:07,780 --> 00:10:11,420
大家可以看一眼，函数是什么

152
00:10:11,430 --> 00:10:14,030
我们刚才讲了，第1坐标定了

153
00:10:14,040 --> 00:10:17,030
第2坐标就定下来

154
00:10:36,940 --> 00:10:40,620
好，我们来看哪些是，这里

155
00:10:41,360 --> 00:10:42,640
F1就不是，为什么

156
00:10:42,650 --> 00:10:48,170
你看，X，1、X，2这个地方不是

157
00:10:48,180 --> 00:10:50,820
X有两个对应的，不对

158
00:10:51,900 --> 00:10:54,920
F2是，F3是

159
00:10:55,270 --> 00:10:56,340
为什么F3是

160
00:10:56,920 --> 00:11:01,350
虽然这里有两个一模一样的

161
00:11:02,400 --> 00:11:06,590
有两个X好像有两个有序对

162
00:11:06,600 --> 00:11:09,310
但实际上这两个在集合里面是一个元素

163
00:11:10,160 --> 00:11:14,070
我们前面讲集合的一个特点是什么

164
00:11:14,080 --> 00:11:16,110
没有相同的元素

165
00:11:16,650 --> 00:11:19,150
所以这两个就是一个

166
00:11:23,420 --> 00:11:25,650
所以F3也是函数

167
00:11:26,120 --> 00:11:27,330
F4是函数

168
00:11:31,060 --> 00:11:40,030
只有一个有序对

169
00:11:40,740 --> 00:11:43,670
F5，空集也是函数为什么

170
00:11:45,690 --> 00:11:47,100
刚才讲什么叫函数

171
00:11:48,530 --> 00:11:49,440
什么叫关系

172
00:11:50,300 --> 00:11:52,920
关系是A乘B的子集

173
00:11:53,210 --> 00:11:54,800
空集肯定是关系了

174
00:11:57,430 --> 00:12:03,040
那么它是笛卡尔积的子集

175
00:12:04,110 --> 00:12:04,720
第二个

176
00:12:05,110 --> 00:12:09,250
它们存在不存在第1坐标相同

177
00:12:09,260 --> 00:12:10,090
第2坐标不相同

178
00:12:10,100 --> 00:12:12,530
不存在，它就是函数，只不过这个函数是什么

179
00:12:12,540 --> 00:12:13,250
就是空的

180
00:12:13,810 --> 00:12:15,360
空对空而已

181
00:12:18,360 --> 00:12:19,480
F6是函数

182
00:12:22,990 --> 00:12:26,400
你看，这个没有同样的第1坐标

183
00:12:26,410 --> 00:12:27,960
后面第2个不同，没有的