B树 B+树

1.前言
动态查找树主要有：二叉查找树，平衡二叉查找树，红黑树，B树/B+树。

实际问题：大规模数据存储中，实现索引查询的背景下，树节点存储的元素数量有限，导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁。因此采用多叉树来减少树的深度

B树就是是平衡多路查找树结构

2 外存储器-磁盘
2.1 磁盘构造

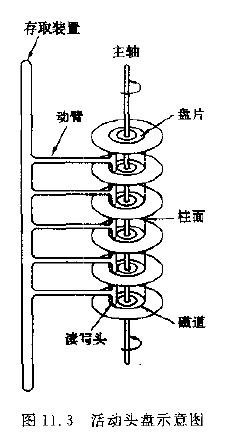
当盘片绕主轴旋转的时候，磁头与旋转的盘片形成一个圆柱体，各个盘面上半径相同的磁道组成了一个圆柱面，称之为柱面。因此，柱面的个数也就是盘面上的磁道数
2.2磁盘的读写原理和效率
读/写磁盘上某一指定数据需要下面3个步骤：
(1) 首先移动臂根据柱面号使磁头移动到所需要的柱面上，这一过程被称为定位或查找 。
(2) 如上图11.3中所示的6盘组示意图中，所有磁头都定位到了10个盘面的10条磁道上(磁头都是双向的)。这时根据盘面号来确定指定盘面上的磁道。
(3) 盘面确定以后，盘片开始旋转，将指定块号的磁道段移动至磁头下。

访问具体信息的时间组成：
● 查找时间(seek time) Ts: 完成上述步骤(1)所需要的时间。这部分时间代价最高，最大可达到0.1s左右。
● 等待时间(latency time) Tl: 完成上述步骤(3)所需要的时间。由于盘片绕主轴旋转速度很快，一般为7200转/分(电脑硬盘的性能指标之一, 家用的普通硬盘的转速一般有5400rpm(笔记本)、7200rpm几种)。因此一般旋转一圈大约0.0083s。
● 传输时间(transmission time) Tt: 数据通过系统总线传送到内存的时间，一般传输一个字节(byte)大概0.02us=2*10^(-8)s

所以尽量把相关信息存在同一盘块，同一磁盘或者至少放在同一柱面或相邻磁道上，以求再读写信息时尽量减少磁头来回移动的次数，避免过多的查找时间Ts。

在大规模数据存储在外存磁盘中，而外存磁盘中读取和读写数据时，先定位到磁盘的某块，如果找到一种合理高效的外存数据结构有效地查找磁盘中的数据？

3 B树
1 B树的定义
B-tree树就是B树

B树与红黑树最大的不同在于，B树的结点可以有许多子女，从几个到几千个。那为什么又说B树与红黑树很相似呢?因为与红黑树一样，一棵含n个结点的B树的高度也为O（lgn），但可能比一棵红黑树的高度小许多，应为它的分支因子比较大。所以，B树可以在O（logn）时间内，实现各种如插入（insert），删除（delete）等动态集合操作。

B 树又叫平衡多路查找树。一棵m阶的B 树的性质如下：

1)树中每个结点最多含有m个孩子（m>=2）；

2)除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；

3)若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；

4)所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null)；

5)每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，……，Kn，Pn)。其中：
a) Ki (i=1…n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。

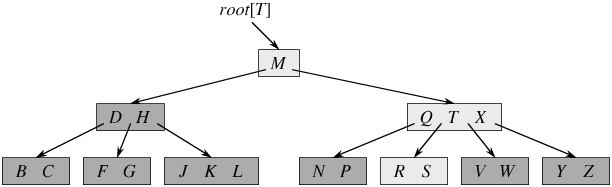
2 B树的类型和节点定义:

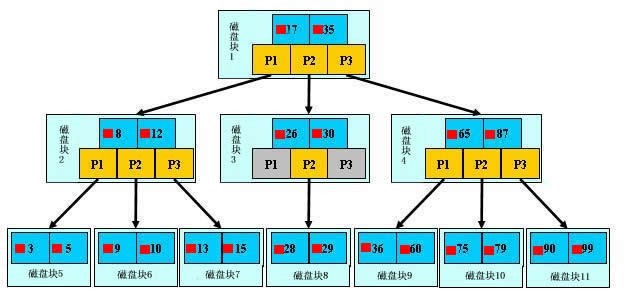
3 文件查找过程
查找文件29的过程：

1)根据根结点指针找到文件目录的根磁盘块1，将其中的信息导入内存。【磁盘IO操作 1次】

2)此时内存中有两个文件名17、35和三个存储其他磁盘页面地址的数据。根据算法我们发现：17<29<35，因此我们找到指针p2。

3)根据p2指针，我们定位到磁盘块3，并将其中的信息导入内存。【磁盘IO操作 2次】

4)此时内存中有两个文件名26，30和三个存储其他磁盘页面地址的数据。根据算法我们发现：26<29<30，因此我们找到指针p2。

5)根据p2指针，我们定位到磁盘块8，并将其中的信息导入内存。【磁盘IO操作 3次】

6)此时内存中有两个文件名28，29。根据算法我们查找到文件名29，并定位了该文件内存的磁盘地址。

总共需要3次磁盘IO操作和3次内存查找，内存中的文件可以使用折半查找提高效率。

如果使用平衡二叉树进行查找，磁盘4次，最多五次，而且文件越多，B树比二叉树所用的磁盘IO次数越少，效率越高

4 树的高度
若B树某一非叶子节点包含N个关键字，则此非叶子节点含有N+1个孩子结点，而所有的叶子结点都在第I层，我们可以得出：

1. 因为根至少有两个孩子，因此第2层至少有两个结点。
2. 除根和叶子外，其它结点至少有┌m/2┐个孩子，
3. 因此在第3层至少有2*┌m/2┐个结点，
4. 在第4层至少有2*(┌m/2┐^2)个结点，
5. 在第 I 层至少有2*(┌m/2┐^(l-2) )个结点，于是有： N+1 ≥ 2*┌m/2┐I-2；
6. 考虑第L层的结点个数为N+1，那么2*(┌m/2┐^(l-2)）≤N+1，也就是L层的最少结点数刚好达到N+1个，即： I≤ log┌m/2┐((N+1)/2 )+2；

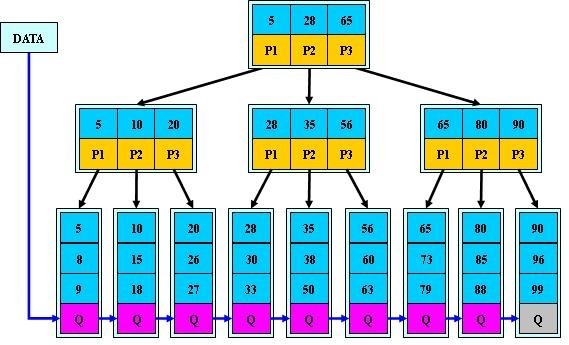
4 B+树
一棵m阶的B+树和m阶的B树的异同点在于：
1.有n棵子树的结点中含有n-1 个关键字； (此处颇有争议，B+树到底是与B 树n棵子树有n-1个关键字 保持一致，还是不一致：B树n棵子树的结点中含有n个关键字，待后续查证。)
2.所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3.所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B 树的非终节点也包含需要查找的有效信息)

为什么说B+树比B树更适合实际应用中操作系统的文件索引和数据索引？
B+树的内部节点没有指向关键字具体信息的指针。因此其内部节点相对B树更小。因此盘块所能容纳的关键字数量也越多，相对来说IO读写次数也就降低了。

举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+ 树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B 树就比B+ 树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

数据库索引采用B+树的主要原因是 B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。正是为了解决这个问题，B+树应运而生。B+树只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作（或者说效率太低）。