Chapter 6: Trees Part II

Chapter 6: Trees Part II

5. Generic Trees (N-ary Trees)

Representation

Parent - Children Representation

struct TreeNode{
	int data;
	int father;
	vector<int> children;
};

First Child - Next Sibling Representation

The main idea is if we have a link between children then we do not need extra links from parent to all children.

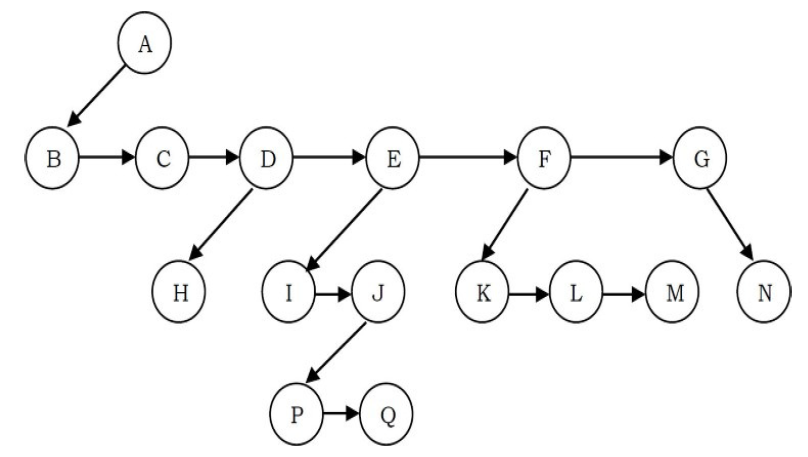
struct TreeNode{
	int data;
	struct TreeNode *firstChild;
	struct TreeNode *nextSibling;
};

Since we are able to convert any generic tree to binary representation; in practice we use binary trees. We can treat all generic trees with a first child / next sibling representation as binary trees.

Traversal

Depth First Search

/*root first traversal*/
void dfs(int root){
	/*1. process on the current node*/
	printf("%d", root.data);
	/*2. extend new node*/
	for(int i=0; i<tree[root].children.size(); i++)
		dfs(tree[root].children[i];
}

Breath First Search

/*level order traversal*/
void bfs(int root){
	queue<int> q;
	q.enqueue(root);
	while(!q.empty()){
		/*1. process on the current node*/
		int k=q.front();
		q.dequeue();
		/*2. extend new node*/
		for(int i=0; i<tree[k].children.size(); i++)
			q.enqueue(tree[k].children[i]);
	}
}	

---

6. Generic Trees: Problems & Solution

Pro 1: Find the Sum of All Elements

Solution :

int FindSum(struct TreeNode *root){
	if(!root) return 0;
	return root->data + FindSum(root->firstChild) + FindSum(root->nextSibling);
}

Pro 2: What’s the Minimum / Maximum Height

Solution :

For a 4-ary tree (each node can contain maximum of 4 children),

• The maximum possible height with n nodes is $n-4$. If we have a restriction at least one node has 4 children, then we keep one node with 4 children and the remaining nodes with one child.
• The maximum possible height with n nodes is $lo{g}_4(3n+1)-1$. For a given height h the maximum possible nodes are $n=\frac{4^{h+1}-1}{3}$, take logarithm on both sides.

Pro 3: Find the Height / Depth of Tree

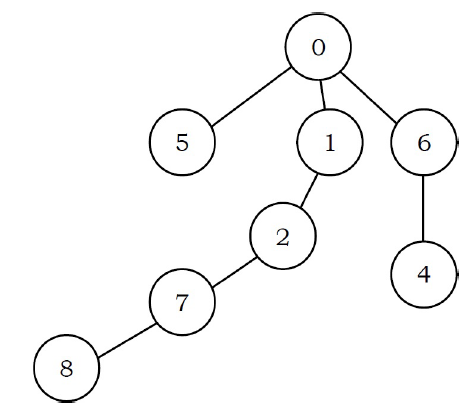
Given a parent array P, where P[i] indicates the parent of i^th node in the tree (assume parent of root node is indicated with -1).

If the P is

0	1	2	3	4	5	6	7	8
-1	0	1	6	6	0	0	2	7

Its corresponding tree is

Solution :

• Start at every node and keep going to its parent until we reach -1 and also keep track of the maximum depth among all nodes.

int FindDepth(int P[], int n){
	int maxDepth=-1, currDepth=-1, j;
	for(int i=0; i<n; ++i){
		currDepth=0;
		j=i;
		while(P[j]!=-1){
			currDepth++;
			j=P[j];
		}
		maxDepth=fmax(currDepth, maxDepth);
	}
	return maxDepth;
}

• Time Complexity: O(n²). For skew tree we will be re-calculating the same value. Space Complexity: O(1).
• We can store the previous calculated node’s depth in hash table or other array to reduce the time complexity but uses extra space.

Pro 4.1: Count the Number of Siblings

Solution :

int SiblingCount(struct TreeNode *node){
	int count=0;
	while(node){
		count++;
		node=node->nextSibling;
	}
	return count;
}

Pro 4.2: Count the Number of Children

Solution :

int ChildrenCount(struct TreeNode *node){
	int count=0;
	node=node->firstChild;
	while(node){
		count++;
		node=node->nextSibling;
	}
	return count;
}

Pro 5.1: Check Whether the Trees are Isomorphic

Two trees are isomorphic if they have the same structure and the values of the nodes does not affect whether two trees are isomorphic or not.

Solution :

int IsIsomorphic(struct TreeNode *root1, struct TreeNode *root2){
	if(!root1 &&! root2) 
		return 1;
	if((!root1 && root2) || (root1 && !root2))
		return 0;
	return(IsIsomprphic(root1->firstChild, root2->firstChild) && IsIsomorphic(root1->nextSibling, root2->nextSibling);
}

Pro 5.2: Check Whether the Trees are Quasi-isomorphic

Trees are quasi-isomorphic if root1 can be transformed into root2 by swapping the left and right children of some of the nodes of root1. Data are not important in determining quasi-isomorphic.

Solution :

int QuasiIsomorphic(struct TreeNode *root1, struct TreeNode *root2){
	if(!root1 && !root2) 
		return 1;
	if((!root1 && root2) || (root1 && !root2))
		return 0;
	return(QuasiIsomorphic(root1->firstChild, root2->firstChild) && QuasiIsomorphic(root1->nextSibling, root2->nextSibling) || QuasiIsomorphic(root1->nextSibling, root2->firstChild) && QuasiIsomorphic(root1->firstChild, root2->nextSibling));
}

Pro 6: Construct Full k-ay Tree

A full k-ary tree is a tree where each node has either 0 or k children. Given an array which contains the preorder traversal of full k-ary tree, give an algorithm for constructing the full k-ary tree.

Solution :

• In k-ary tree, for a node at i^th position its children will be at k*i+1 to k*i+k.
• To construct a full k-ary tree, we just need to keep on creating the nodes without bothering about the previous constructed nodes. We can use this trick to build the tree recursively by using one global index.

struct karyTreeNode{
	char data;
	struct karyTreeNode *child[];
};
int *Ind=0;																//global index
struct karyTreeNode *BuildKTree(char A[], int n, int k){
	if(n<=0) return NULL;
	struct KaryTreeNode *newNode=(struct karyTreeNode*)malloc(sizeof(struct karyTreeNode));
	if(!newNode) return; 								//memory error
	newNode->child=(struct karyTreeNode *)malloc(k * sizeof(struct karyTreeNode));
	if(!newNode->child) return ;						//memory error
	newNode->data=A[Ind];
	for(int i=0; i<k; i++){
		if(k*Ind+i<n){
			Ind++;
			newNode->child[i]=BuildKTree(A, n, Ind);					// n size of preorder array
		}
		else newNode->child[i]=NULL;
	}
	return newNode;
}

• Time Complexity: O(n). where n is the size of the pre-order array because we are moving sequentially and not visiting the already constructed nodes.

---

7. Threaded Binary Tree Traversal

In the previous sections we have seen that, preorder, inorder, postorder used stacks and level order traversals used queues as auxiliary data structure.This section we will discuss threaded binary tree traversals or stack/queue–less traversals.

Issues with Binary Tree Traversals

• The storage space required for the stack and queue is large.
• The majority of pointers in any binary tree are NULL. For example, a binary tree with n nodes has n+1 NULL pointers and these were wasted.
• It is difficult to find successor node for a given node.

Threaded Binary Tree Structure

The common convention is to store predecessor / successor information in NULL pointers which called threads. If we store predecessor information in NULL left pointers and successor information in NULL right pointers, then we can call such binary trees fully threaded binary trees or simply threaded binary tree. We can also only store either predecessor information in NULL left pointers (left threaded binary trees) or successor information in NULL right pointers (right threaded binary trees). Two additional fields (Ltag and Rtag) in each node are used for differentiating between a regular left/right pointer and a thread.

struct ThreadedBinaryTreeNode{
	struct ThreadedBinaryTreeNode *left;
	struct ThreadedBinaryTreeNode *right;
	int Ltag;								//if ltag==1, left child; if ltag==0, inorder predecessor
	int Rtag;								//if rtag==1, right child; if rtag==0, inorder successor 
	int data;
};
/*also can define preorder or postorder*/

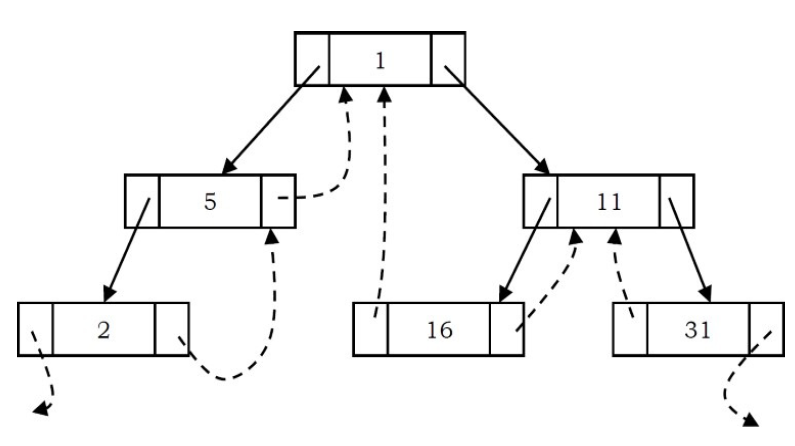
What should leftmost and rightmost pointers point to?

In the representations of a threaded binary tree, it is convenient to use a special node Dummy which is always present even for an empty tree. Node that right tag of Dummy node is 1 and its right child points to itself.

Operations

Find Inorder Successor in Inorder Threaded Binary Tree

struct ThreadedBinaryTreeNode *InorderSuccessor(struct ThreadedBinaryTreeNode *p){
	struct ThreadedBinaryTreeNode *pos;
	if(p->Rtag==0)							//has no right subtree
		return p->right;				
	else{									//has right subtree
		pos=p->right;
		while(pos->Ltag==1)					//the LEFT OF the nearest node whose left subtree contains p 
			pos=pos->left;					//in other word, the leftmost node in the right subtree of p
		return pos;
	}
}

Find PreOrder Successor in Inorder Threaded Binary Tree

struct ThreadedBinaryTreeNode *PreorderSuccessor(struct ThreadedBinaryTreeNode *p){
	struct ThreadedBinaryTreeNode *pos;
	if(p->Ltag==1)							//has left subtree
		return p->left;
	else{									//has no left tree
		pos=p;
		while(pos->Rtag==0)					//eg:find node2's successor in previous figure
			pos=pos->right;
		return pos->right;      			//the Right child of the nearest node whose right subtree contains p
	}										//in short right child 
}

Inorder Traversal in Inorder Threaded Binary Tree

void InorderTravesal(struct ThreadedBinaryTreeNode *dummy){			//start with dummy node and call InorderSuceesor() 
	struct ThreadedBinaryTreeNode *p=InorderSuccessor(dummy);		//*p=root	
	while(p!=dummy){												//loop until reach dummy node
		p=InorderSuccessor(p);
		printf("%d", p->data);
	}
}

PreOrder Traversal of InOrder Threaded Binary Tree

void PreoederTraversal(struct ThreadedBinaryTreeNode *dummy){
	struct ThreadedBinaryTreeNode *p;
	p=PreorderSuccessor(dummy);
	while(p!=dummy){
		p=PreorderSuccessor(p);
		printf("%d", p->data);
	}
}

Note

Inorder and Preorder successor finding is easy with threaded binary trees. But finding Postorder successor is very difficult if we do not use stack.

Insertion of Nodes in InOrder Threaded Binary Trees

Assume we want to attach Q to right of P.

• Case 1: Node P has no right child
  Just attach Q to P and change its left and right pointers.
  
• Case 2: P has right child
  Traverse R’s subtree and find the leftmost node and then update the left and right pointer of that node.
  

void InsertRightInInorderTBT(struct ThreadedBinaryTreeNode *p, struct ThreadedBinaryTreeNode *Q){
	struct ThreadedBinaryTreeNode *temp;
	Q->right=P->right; Q->Rtag=P->Rtag;
	Q->left=P; Q->Ltag=0;
	P->right=Q;	P->Rtag=1;
	if(Q->Rtag==1){
		temp=Q->right;
		while(Temp->Ltag)
			temp=temp->left;
		temp->left=Q;
	}
}

---

8. Threaded Binary Trees: Problems & Solutions

Pro 1: Find the PreOrder Successor without Thread

Solution : auxiliary stack

• On the first call, the parameter node is a pointer to the root of the tree, and thereafter its value is NULL. Since we are simply asking for the successor of the node we got the last time we called the function.
• It is necessary that the contents of the stack S and the pointer P to the last node “visited” are preserved from one call of the function to the next; they are defined as static variables.

/*PreOrder successor for an unthreaded binary tree*/
static struct BinaryTreeNode *p;
static Stack *s=CreateStack();		
struct BinaryTreeNode *PreorderSuccessor(struct BinaryTreeNode *node){
	if(node!=NULL)
		p=node;
	if(p->left!=NULL){					//has left subtree
		Push(s, p);
		p=p->left;
	}
	else{								//has no left subtree
		while(p->right==NULL)
			p=Pop(s);				
		p=p->right;
	}
	return p;
}
/*the function is a loop form implement by such call
while(node)
	PreorderSuccessor(node);
it traverse the tree like recursion but implement by a stack and loop
*/

Pro 2. Find the InOrder Successor without Thread

Solution :

static struct BinaryTreeNode *p;
static Stack *s=CreateStack();
struct BinaryTreeNode *InorderSuccessor(struct BinaryTreeNode *node){
	if(node!=NULL)
		p=node;
	if(p->right==NULL)
		p=Pop(s);
	else{
		p=p->right;
		while(p->left!=NULL)
			Push(s, p);
		p=p->left;
	}
	return p;
}

---

9. Expression Trees

A tree representing an expression is called an expression tree and its leaf nodes are operands and non-leaf nodes are operators.

Build Expression Tree from Postfix Expression

struct BinaryTreeNode *BuildExprTree(char postfixExpr[], int size){
	struct Stack *s=Stack(size);
	for(int i=0; i<size; i++){
		if(postfixExpr[i] is an operand){
			struct BinaryTreeNode *newNode=(struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
			if(!newNode) return NULL; 			//memory error
			newNode->data=postfixExpr[i];
			newNode->left=newNode->right=NULL;
			Push(s, newNode);
		}
		else{
			struct BinaryTreeNode *t2=Pop(s), *t1=Pop(s);
			struct BinaryTreeNode *newNode=(struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
			if(!newNode) return NULL; 			//memory error
			newNode->data=postfixExpr[i];
			newNode->left=t1;
			newNode->right=t2;
			Push(s, newNode);
		}
	}
	return s;
}		

---

10. XOR Trees

Like threaded binary trees XOR tree does not need stacks or queues for traversing the tree. This representation is used for traversing back (to parent) and forth (to children) using $\oplus$ operation.

• Each nodes left / right will have the $\oplus$ of its parent and its left / right children.
• The root nodes parent is NULL and also leaf nodes children are NULL nodes.

The major objective of its presentation is the ability to move to parent by perform $\oplus$ on its child and corresponding pointer’s information, as well to children by perform $\oplus$ on its parent and corresponding pointer’s information.