tan (pi/4) = 1
pi/4 = arctan 1
pi = 4arctan 1
反三角函数的定积分
积分其导数并固定在一点上的值给出反三角函数作为定积分的表达式:
当 x 等于 1 时,在有极限的域上的积分是瑕积分,但仍是良好定义的。
一个看起来很牛的计算Pi的程序:
int a=10000,b,c=2800,d,e,f[2801],g;
main() {
for(;b-c;)
f[b++]=a/5;
for(;d=0,g=c*2;c -=14,printf("%.4d",e+d/a),e=d%a)
for(b=c; d+=f[b]*a,f[b]=d%--g,d/=g--,--b; d*=b);
}
这还不是最牛的,源码所在的这个网站里牛程序多的是:
http://numbers.computation.free.fr/Constants/TinyPrograms/tinycodes.html
下面是用C写的Pi计算程序:
The following tiny C code computes digits of p. Boris Gourevitch kindly sent me the information that this program is from Dik T. Winter (cwi institute, Holland).
int a=10000,b,c=8400,d,e,f[8401],g;main(){
for(;b-c;)f[b++]=a/5;
for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)
for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);}
The program has 158 characters long. Finding the algorithm used is not so easy. Sebastian Wedeniws worked hard to find a shorter program (142 characters) :
main(){int a=1e4,c=3e3,b=c,d=0,e=0,f[3000],g=1,h=0;
for(;b;!--b?printf("%04d",e+d/a),e=d%a,h=b=c-=15:f[b]=
(d=d/g*b+a*(h?f[b]:2e3))%(g=b*2-1));}
Jean-Charles Meyrignac pointed me out a tiny code from the page http://www.isr.umd.edu/~jasonp/pigjerr. The program is by Gjerrit Meinsma, of 141 characters long, and computes 1000 digits of pi.
long k=4e3,p,a[337],q,t=1e3;
main(j){for(;a[j=q=0]+=2,--k;)
for(p=1+2*k;j<337;q=a[j]*k+q%p*t,a[j++]=q/p)
k!=j>2?:printf("%.3d",a[j-2]%t+q/p/t);}
二、矩阵拟合法计算Pi - 可用OpenMP并行
Sequetial Version:
#include <stdio.h>
#include <time.h>
void main ()
{
time_t start, finish;
static long num_steps = 1000000000;
double step;
int i;
double x, pi, sum = 0.0;
step = 1.0/(double) num_steps;
start = clock();
for (i=0;i < num_steps; i++)
{
x = (i+0.5)*step;
sum = sum + 4.0/(1.0+x*x);
}
pi = step * sum;
finish = clock();
printf( "Pi = %16.15f (%d steps), %ld ms\n ", pi, num_steps, finish-start );
return;
}
--------------------------------------------------------------------------------------------
Parallel Version:
#include <stdio.h>
#include <time.h>
#include <omp.h>
void main ()
{
time_t start, finish;
static long num_steps = 1000000000;
double step;
int i;
double x, pi, sum = 0.0;
step = 1.0/(double) num_steps;
start = clock();
#pragma omp parallel for reduction(+:sum) private(x) /*只加了这一句,其他不变*/
for (i=0;i < num_steps; i++)
{
x = (i+0.5)*step;
sum = sum + 4.0/(1.0+x*x);
}
pi = step * sum;
finish = clock();
printf( "Pi = %16.15f (%d steps), %ld ms\n ", pi, num_steps, finish-start );
return;
}
result:
Sequential version:
Pi = 3.141592653589792 (1000000000 steps), 13900000 ms
Parallel version for 8 threads:
Pi = 3.141592653589794 (1000000000 steps), 1820000 ms
从结果可以看到8线程的speedup=7.64,接近线性。因为这个程序本身具有良好的并发性,循环间几乎没有数据依赖,除了sum,但是用reduction(+:sum)把对于sum的相关也消除了。而且实验平台本身就有8个处理器核。
三、概率方法
Name: 蒙特卡罗法求解 pi
Description:
边长为r的正方形,内接1/4圆周,半径也为r.
正方形面积s1 = r*r
1/4圆周面积s2 = pi*r*r / 4
假设在正方形中随机选择许多点,那么这些点中有一部分也落在1/4圆周内。
如果所选择的点是均匀分布的,那么我们可以期望落于1/4圆周内的点的概率是:
f = s2 / s1 = pi / 4
因此,通过测定f , 就可以计算出 pi = 4*f .
程序如下:
#include<iostream.h>
#define for if(0);else for
static long int seed = 1L;
static long int const a =16807L, m = 2147483647L, q = 127773L, r = 2836L;
double Rondom()
{
seed = a*(seed%q) - r*(seed/q);
if( seed < 0 )
seed += m;
return (double) seed / (double) m;
}
double Pi(unsigned int trials)
{
unsigned int hits = 0;
for(unsigned int i=0;i<trials;++i)
{
double const x = Rondom();
double const y = Rondom();
cout<<x<<' '<<y<<endl;
if(x*x+y*y<1.0)
++hits;
}
return 4.0 * hits / trials;
}
int main()
{
unsigned int t;
while(cin>>t){
double pi = Pi(t);
cout.precision(20);
cout<< pi <<endl;
}
}
忘记注释下!
就是输入的t 就是trials 越大,越准确,当然时间也越长了!
输出7位,还是要耗点时间的!
这个方法比较慢,用于测试计算性能应该还不错。
四、数学公式
数学家们研究了数不清的方法来计算PI,这个程序所用的公式如下:
1 2 3 k
pi = 2 + --- * (2 + --- * (2 + --- * (2 + ... (2 + ---- * (2 + ... ))...)))
3 5 7 2k+1
就是
Pi/2 = Sum{k!/(2k+1)!!, k=0,1,2,...}
五、级数
还有使用级数的:
其中有些计算起来很复杂, 我们可以选用第三个, 比较简单, 并且收敛的非常快。
因为计算π值, 而这个公式是计算π/2的, 我们把它变形:
π = 2 + 2/3 + 2/3*2/5 + 2/3*2/5*3/7 + ...
对于级数, 我们先做个简单测试, 暂时不要求精度:
用 C++ Builder 新建一个工程, 在 Form 上放一个 Memo1 和 一个 Button1, 在 Button1 的 OnClick 事件写:
| void __fastcall TForm1::Button1Click(TObject *Sender) { double x=2, z=2; int a=1, b=3; while(z>1e-15) { z = z*a/b; x += z; a++; b+=2; } Memo1->Text = AnsiString().sprintf("Pi=%.13f", x); } |
按Button1在Memo1显示出执行结果:
Pi=3.1415926535898
这个程序太简单了, 而且 double 的精度很低, 只能计算到小数点后 10 几位。
把上面的程序改造一下, 让它精确到小数点后面 1000 位再测试一下:
在 Form 上再放一个按钮 Button2, 在这个按钮的 OnClick 事件写:
| void __fastcall TForm1::Button2Click(TObject *Sender) { const ARRSIZE=1010, DISPCNT=1000; //定义数组大小,显示位数 char x[ARRSIZE], z[ARRSIZE]; //x[0] x[1] . x[2] x[3] x[4] .... x[ARRSIZE-1] int a=1, b=3, c, d, Run=1, Cnt=0; memset(x,0,ARRSIZE); memset(z,0,ARRSIZE); x[1] = 2; z[1] = 2; while(Run && (++Cnt<200000000)) { //z*=a; d = 0; for(int i=ARRSIZE-1; i>0; i--) { c = z[i]*a + d; z[i] = c % 10; d = c / 10; } //z/=b; d = 0; for(int i=0; i<ARRSIZE; i++) { c = z[i]+d*10; z[i] = c / b; d = c % b; } //x+=z; Run = 0; for(int i=ARRSIZE-1; i>0; i--) { c = x[i] + z[i]; x[i] = c%10; x[i-1] += c/10; Run |= z[i]; } a++; b+=2; } Memo1->Text = AnsiString().sprintf("计算了 %d 次\r\n",Cnt); Memo1->Text = Memo1->Text + AnsiString().sprintf("Pi=%d%d.\r\n", x[0],x[1]); for(int i=0; i<DISPCNT; i++) { if(i && ((i%100)==0)) Memo1->Text = Memo1->Text + "\r\n"; Memo1->Text = Memo1->Text + (int)x[i+2]; } } |
按 Button2 执行结果:
Pi=03.
1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
4428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273
7245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094
3305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912
9833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132
0005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235
4201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859
5024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303
5982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989
这下心理有底了, 是不是改变数组大小就可以计算更多位数呢?答案是肯定的。
如果把定义数组大小和显示位数改为:
const ARRSIZE=10100, DISPCNT=10000; //定义数组大小,显示位数
执行结果精度可达 10000 位:
Pi=03.
1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
4428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273
7245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094
3305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912
9833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132
0005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235
4201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859
5024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303
5982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989
3809525720106548586327886593615338182796823030195203530185296899577362259941389124972177528347913151
... 限于篇幅, 这里就省略了, 还是留给你自己来算吧!
5020141020672358502007245225632651341055924019027421624843914035998953539459094407046912091409387001
2645600162374288021092764579310657922955249887275846101264836999892256959688159205600101655256375678
提高精度的原理:
以上程序的原理是利用数组把计算结果保存起来, 其中数组每一项保存10进制数的一位,
小数点定位在数组第1个数和第二个数之间, 即小数点前面2位整数, 其余都是小数位。
利用电脑模拟四则运算的笔算方法来实现高精度的数据计算,没想到最原始的方法竟然是精度最高的。











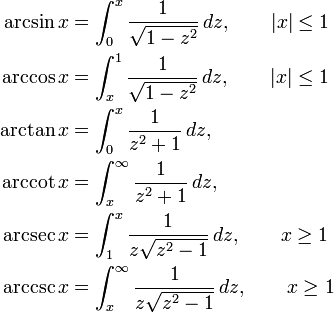

















 796
796

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








