机器学习算法系列（十）-线性判别分析算法（一）（Linear Discriminant Analysis Algorithm）

阅读本文需要的背景知识点：拉格朗日乘数法、一丢丢编程知识

一、引言

  前面学习了一种用回归的方式来做分类的算法——对数几率回归算法，下面再来学习另一种分类算法——线性判别分析算法¹（Linear Discriminant Analysis Algorithm / LDA），该算法由罗纳德·艾尔默·费希尔在1936年提出，所以也被称为费希尔的线性鉴别方法（Fisher’s linear discriminant）

二、模型介绍

  先来看下图，假设有二分类的数据集，“+”表示正例，“-”表示反例。线性判别分析算法就是要设法找到一条直线，使得同一个类别的点在该直线上的投影尽可能的接近，同时不同分类的点在直线上的投影尽可能的远。该算法的主要思想总结来说就是要“类内小、类间大”，非常类似于在软件设计时说的“低耦合、高内聚”。

来源：《机器学习》-周志华

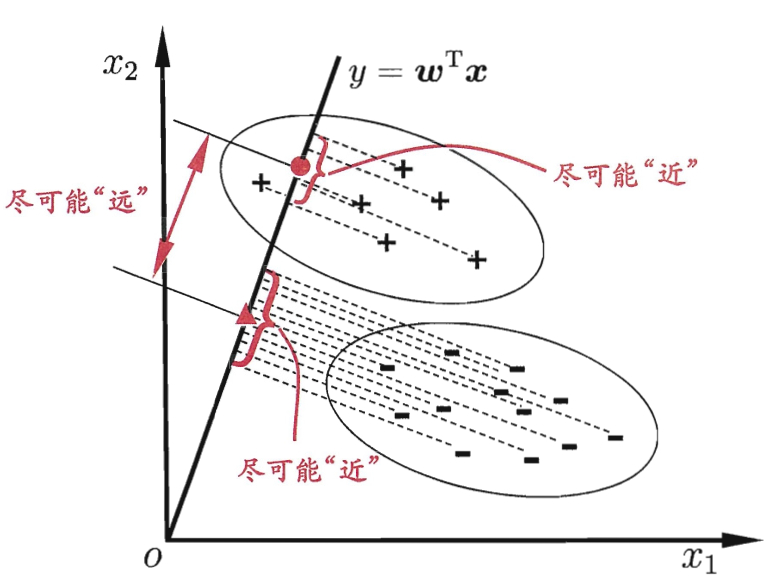
  当有新的样本点需要分类时，计算该点在直线上的投影，根据投影的位置来判断新样本点的分类。那么如何用数学公式来表示上述说法呢？

三、代价函数

  假设有样本数为 N 的数据集，$X_i$表示第i个样本点的特征向量，$y_i$表示第i个样本点的标签值，$w$ 表示直线的权重系数。

样本点到直线的投影向量

（1）投影向量为样本点乘以与直线夹角的余弦值
（2）带入夹角余弦值的公式
（3）由上图可以看到，我们只需要关系该直线的斜率即可，也就是 $w$ 的方向。不妨令w为单位向量，即$|w|=1$，带入后整理可得
（4）可以看到（3）式中的第一项即为单位向量，后两项乘积为实数。投影的方向必然与 $w$ 的方向相同，所以不妨将第一项用 $w$ 向量代替
$$\begin{array}{rlr}{p}_i& =X_i\cos \theta & (1)\\ & =X_i\frac{w^T{X}_i}{\mid w\mid \mid X_i\mid }& (2)\\ & =\frac{X_i}{\mid X_i\mid }{w}^T{X}_i& (3)\\ & =w^T{X}_{i}w& (4)\end{array}$$

均值向量与协方差矩阵

（1）样本为二分类，$N_1$表示第一类样本数量，$N_2$表示第二类样本数量
（2）第一类样本点投影的均值向量
（3）第一类样本点投影的协方差矩阵
（4）第二类样本点投影的均值向量
（5）第二类样本点投影的协方差矩阵
$$\begin{array}{rlr}N& =N_1+N_2& (1)\\ {\mu }_{p_1}& =\frac{1}{N_1}\sum _{i=1}^{N_1}{p}_i& (2)\\ {\sigma }_{p_1}& =\frac{1}{N_1}\sum _{i=1}^{N_1}\left(p_i-{\mu }_{p_1}\right){\left(p_i-{\mu }_{p_1}\right)}^T& (3)\\ {\mu }_{p_2}& =\frac{1}{N_2}\sum _{i=1}^{N_2}{p}_i& (4)\\ {\sigma }_{p_2}& =\frac{1}{N_2}\sum _{i=1}^{N_2}\left(p_i-{\mu }_{p_2}\right){\left(p_i-{\mu }_{p_2}\right)}^T& (5)\end{array}$$

代价函数

  我们知道样本点的协方差可以用于衡量两个变量的总体误差，那么可以使用协方差的大小来表示类内。而样本点的均值点可以用来表示相对位置，那么可以使用均值点来表示类间。我们的目标是让投影的“类内小、类间大”，那么可以写出对应的代价函数如下：
$$\mathrm{Cost}(w)=\frac{{\left(w^T{\mu }_{p_1}-w^T{\mu }_{p_2}\right)}^2}{w^T{\sigma }_{p_1}w+w^T{\sigma }_{p_2}w}$$

  分子为均值向量大小之差的平方，该值越大代表类间越大。分母为两类样本点的协方差之和，该值越小代表类内越小，我们的目标就是求使得该代价函数最大时的w：
$$w=\underset{w}{\mathrm{argmax}}\left(\frac{{\left(w^T{\mu }_{p_1}-w^T{\mu }_{p_2}\right)}^2}{w^T{\sigma }_{p_1}w+w^T{\sigma }_{p_2}w}\right)$$

  我们先来看下代价函数分子的部分：
（1）将投影的均值向量带入分子中
（2）可以将公共的 $w$ 的转置与$w$ 提出来，观察后可以写成两类样本点的均值向量之差
（3）中间两项为实数可以提到前面，$w$ 为单位向量，与自己相乘为1
（4）将平方写成向量乘积的形式
$$\begin{array}{rlr}{\left(w^T{\mu }_{p_1}-w^T{\mu }_{p_2}\right)}^2& ={\left(w^T\left(\frac{1}{N_1}\sum _{i=1}^{N_1}{w}^T{X}_{i}w\right)-w^T\left(\frac{1}{N_2}\sum _{i=1}^{N_2}{w}^T{X}_{i}w\right)\right)}^2& (1)\\ & ={\left(w^T\left(w^T\left({\mu }_1-{\mu }_2\right)w\right)\right)}^2& (2)\\ & ={\left(w^T\left({\mu }_1-{\mu }_2\right)\right)}^2& (3)\\ & =w^T\left({\mu }_1-{\mu }_2\right){\left({\mu }_1-{\mu }_2\right)}^{T}w& (4)\end{array}$$

  再来看下其中一类的协方差矩阵的部分：
（1）协方差矩阵的定义
（2）带入投影向量与投影的均值向量
（3）可以将公共的 $w$ 的转置与 $w$ 提出来，中间改写成样本点向量与样本点均值向量之差
（4）展开后一项的转置，将实数部分写到前面
（5）将两个实数相乘写成向量的乘法并将公共的 $w$ 的转置与 $w$ 提出来
（6）观察中括号中的部分，可以写成样本点的协方差矩阵的形式
$$\begin{array}{rlr}{\sigma }_{p_1}& =\frac{1}{N_1}\sum _{i=1}^{N_1}\left(p_i-{\mu }_{p_1}\right){\left(p_i-{\mu }_{p_1}\right)}^T& (1)\\ & =\frac{1}{N_1}\sum _{i=1}^{N_1}\left(w^T{X}_{i}w-\frac{1}{N_1}\sum _{j=1}^{N_1}{w}^T{X}_{j}w\right){\left(w^T{X}_{i}w-\frac{1}{N_1}\sum _{j=1}^{N_1}{w}^T{X}_{j}w\right)}^T& (2)\\ & =\frac{1}{N_1}\sum _{i=1}^{N_1}\left(w^T\left(X_i-{\mu }_1\right)w\right){\left(w^T\left(X_i-{\mu }_1\right)w\right)}^T& (3)\\ & =\frac{1}{N_1}\sum _{i=1}^{N_1}\left(w^T\left(X_i-{\mu }_1\right)\right)\left(w^T\left(X_i-{\mu }_1\right)\right)w{w}^T& (4)\\ & =\left(w^T\left(\frac{1}{N_1}\sum _{i=1}^{N_1}\left(X_i-{\mu }_1\right){\left(X_i-{\mu }_1\right)}^T\right)w\right)w{w}^T& (5)\\ & =w^T{\sigma }_{1}ww{w}^T& (6)\end{array}$$

  代价函数的分母部分：
（1）带入上式中协方差矩阵
（2）将实数部分提到前面，后面 $w$ 为单位向量，与自己相乘为 1
（3）化简可得
（4）提出公共部分
$$\begin{array}{rlr}{w}^T{\sigma }_{p_1}w+w^T{\sigma }_{p_2}w& =w^T\left(w^T{\sigma }_{1}ww{w}^T\right)w+w^T\left(w^T{\sigma }_{2}ww{w}^T\right)w& (1)\\ & =w^T{\sigma }_{1}w\left(w^{T}w\right)\left(w^{T}w\right)+w^T{\sigma }_{2}w\left(w^{T}w\right)\left(w^{T}w\right)& (2)\\ & =w^T{\sigma }_{1}w+w^T{\sigma }_{2}w& (3)\\ & =w^T\left({\sigma }_1+{\sigma }_2\right)w& (4)\end{array}$$

  代价函数：
（1）代价函数的定义
（2）带入上面推出的分子分母部分
（3）使用 $S_b$、$S_w$ 来代替中间部分，得到新的代价函数
（4）其中 $S_b$ 被称为"类间散度矩阵"（between-class scatter matrix）
（5）其中 $S_w$ 被称为"类内散度矩阵"（within-class scatter matrix）
$$\begin{array}{rlr}\mathrm{Cost}(w)& =\frac{{\left(w^T{\mu }_{p_1}-w^T{\mu }_{p_2}\right)}^2}{w^T{\sigma }_{p_1}w+w^T{\sigma }_{p_2}w}& (1)\\ & =\frac{w^T\left({\mu }_1-{\mu }_2\right){\left({\mu }_1-{\mu }_2\right)}^{T}w}{w^T\left({\sigma }_1+{\sigma }_2\right)w}& (2)\\ & =\frac{w^T{S}_{b}w}{w^T{S}_{w}w}& (3)\\ S_b& =\left({\mu }_1-{\mu }_2\right){\left({\mu }_1-{\mu }_2\right)}^T& (4)\\ S_w& ={\sigma }_1+{\sigma }_2& (5)\end{array}$$

代价函数最优化

（1）代价函数的新形式，为 $S_b$ 与 $S_w$ 的"广义瑞利商²（generalized Rayleigh quotient）"
（2）可以看到代价函数分子分母都是 $w$ 的二次项，所以代价函数与 $w$ 的长度无关，即缩放 $w$ 不影响代价函数，不妨令分母为 1。可以将问题转化为当分母为 1 时，求分子前面加一个负号的最小值。
（3）可以运用拉格朗日乘数法³，引入一个新的变量 $\lambda$，可以将（2）式改写成新的形式
（4）对（3）式求偏导并令其等于零向量
（5）观察后发现 $S_{b}w$ 的方向恒为两类样本点的均值向量之差的方向，不妨令其为 $\lambda$ 倍的两类样本点的均值向量之差
（6）这样就可以求出了 $w$ 的方向

$$\begin{array}{rlr}\mathrm{Cost}(w)& =\frac{w^T{S}_{b}w}{w^T{S}_{w}w}& (1)\\ \Rightarrow & \begin{array}{r}\underset{w}{\min }-w^T{S}_{b}w\\ s.t.w^T{S}_{w}w=1\end{array}& (2)\\ L(w,\lambda )& =-w^T{S}_{b}w+\lambda \left(w^T{S}_{w}w-1\right)& (3)\\ \frac{\partial L(w,\lambda )}{\partial w}& =-2S_{b}w+2\lambda S_{w}w=0& (4)\\ S_{b}w& =\lambda \left({\mu }_1-{\mu }_2\right)& (5)\\ w& =S_w^{-1}\left({\mu }_1-{\mu }_2\right)& (6)\end{array}$$

四、算法步骤

  线性判别分析的核心思想在前面也介绍过——“类内小、类间大”，按照最后求得的公式直接计算即可。
（1）分别计算每一类的均值向量
（2）分别计算每一类的协方差矩阵
（3）计算每类协方差矩阵之和的逆矩阵，可以使用 SVD 矩阵分解来简化求逆的复杂度
（4）带入公式求出权重系数 $w$
  求新样本的分类时，只需判断新样本点离哪一个分类的均值向量更近，则新样本就是哪个分类，如下所示：
$$k=\underset{k}{\mathrm{argmin}}\left|w^{T}x-w^T{\mu }_k\right|$$

五、代码实现

使用 Python 实现线性判别分析（LDA）：

def lda(X, y):
   """
   线性判别分析（LDA）
   args:
       X - 训练数据集
       y - 目标标签值
   return:
       w - 权重系数
   """
   # 标签值
   y_classes = np.unique(y)
   # 第一类
   c1 = X[y==y_classes[0]][:]
   # 第二类
   c2 = X[y==y_classes[1]][:]
   # 第一类均值向量
   mu1 = np.mean(c1, axis=0)
   # 第二类均值向量
   mu2 = np.mean(c2, axis=0)
   sigma1 = c1 - mu1
   # 第一类协方差矩阵
   sigma1 = sigma1.T.dot(sigma1) / c1.shape[0]
   sigma2 = c2 - mu2
   # 第二类协方差矩阵
   sigma2 = sigma2.T.dot(sigma2) / c2.shape[0]
   # 求权重系数
   return np.linalg.pinv(sigma1 + sigma2).dot(mu1 - mu2), mu1, mu2

def discriminant(X, w, mu1, mu2):
   """
   判别新样本点
   args:
       X - 训练数据集
       w - 权重系数
       mu1 - 第一类均值向量
       mu2 - 第二类均值向量
   return:
       分类结果
   """
   a = np.abs(X.dot(w) - mu1.dot(w))
   b = np.abs(X.dot(w) - mu2.dot(w))
   return np.argmin(np.array([a, b]), axis=0)

六、第三方库实现

scikit-learn⁴ 实现线性判别分析：

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# 初始化线性判别分析器
lda = LinearDiscriminantAnalysis()
# 拟合线性模型
lda.fit(X, y)
# 权重系数
w = lda.coef_
# 截距
b = lda.intercept_

  如果你使用 sklearn 提供的线性判别分析的方法，会发现求解出来的结果与上面自己实现的结果不同，这是因为 sklearn 使用的是另一种方法，并有没使用广义瑞利商的形式，而是从概率分布的角度来做分类，后面一节再来介绍该方法。

七、示例演示

  下图展示了存在二种分类时的演示数据，其中红色表示标签值为 0 的样本、蓝色表示标签值为 1 的样本：

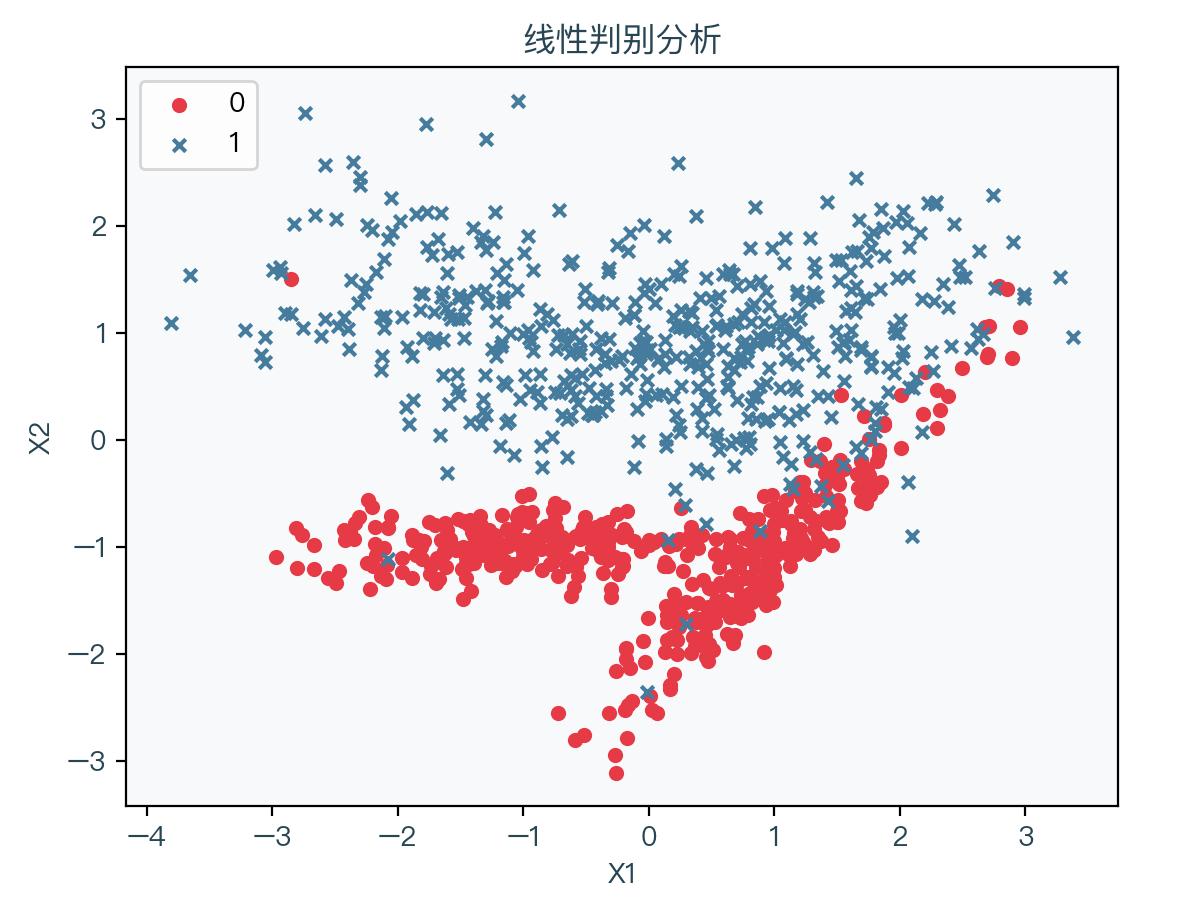
  下图为拟合数据的结果，其中浅红色表示拟合后根据权重系数计算出预测值为 0 的部分，浅蓝色表示拟合后根据权重系数计算出预测值为 1 的部分：

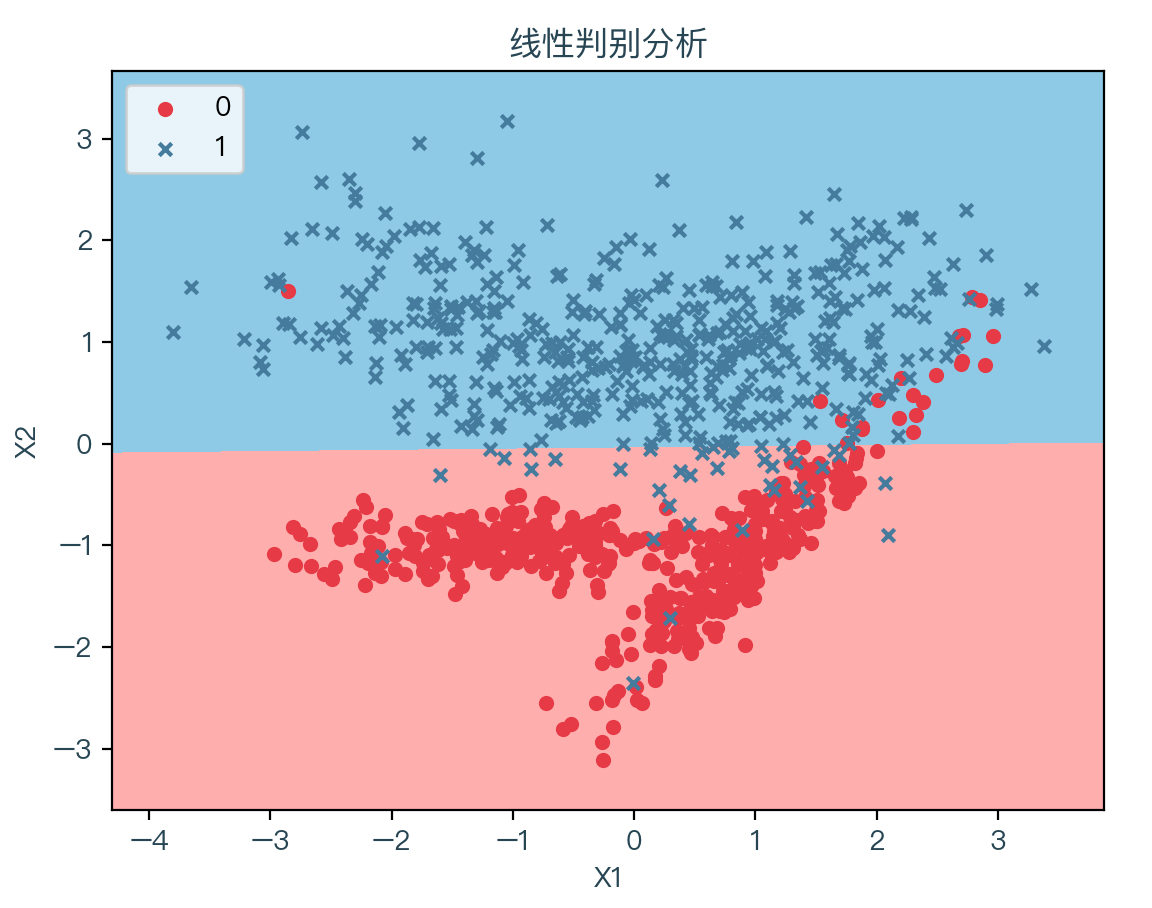
八、思维导图

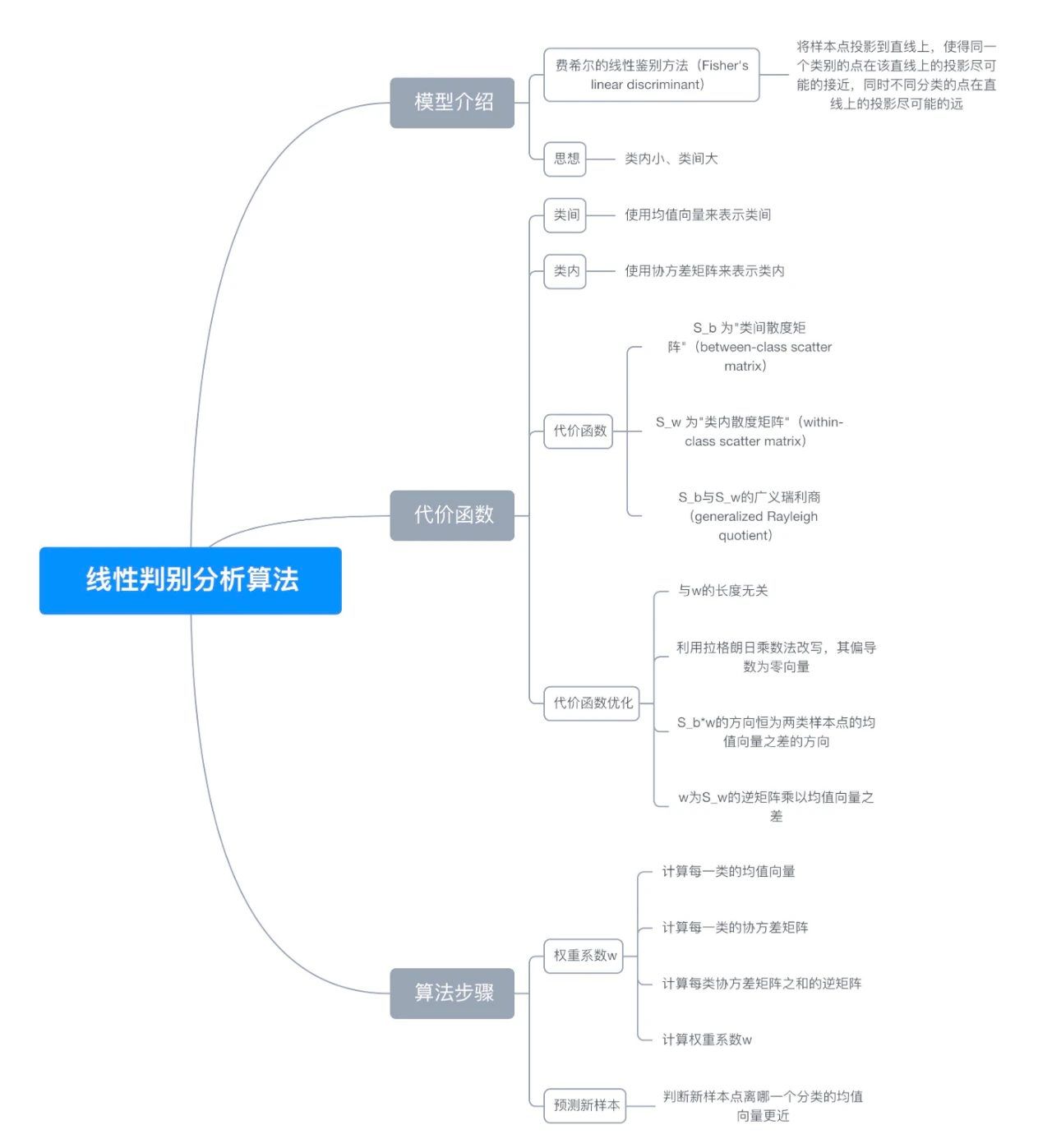
九、参考文献

1. https://en.wikipedia.org/wiki/Linear_discriminant_analysis
2. https://en.wikipedia.org/wiki/Rayleigh_quotient
3. https://en.wikipedia.org/wiki/Lagrange_multiplier
4. https://scikit-learn.org/stable/modules/generated/sklearn.discriminant_analysis.LinearDiscriminantAnalysis.html

完整演示请点击这里

注：本文力求准确并通俗易懂，但由于笔者也是初学者，水平有限，如文中存在错误或遗漏之处，恳请读者通过留言的方式批评指正

本文首发于——AI导图，欢迎关注