2017年11月12题训练日记

       发现博客10点以后提交不上，数论一会就结束 了，下面说一下部分知识点：

快速幂：

 

int pow_mod(int n,int k,int m) //快速幂求n^k余m的结果

{  
    int res=1;  
    n=n%mod;
    while(k>0)  
    {  
        if(k&1)  
            res=res*n%m;  
        n=n*n%m;  
        k>>=1;  
    }  
    return res;  
}  

经常会遇到求一个大数的前几位和后几位，快速幂是可以求后几位的，用log10函数求大数首部数，比如

 

n^k = X *10 ^(len-1)             //len是整数的长度,X是10整数位置只有一位的n^k值的浮点数表示
两边取对数：
K*log10(N)=(len-1)+log10( X )
double tmp=k*log10(n*1.0);  //temp等于左边
tmp=tmp-(long long)tmp;     //因为log(x)小于1，而（len-1）为整数，所以temp减去整数部分就只剩下log10（x）
tmp=pow(10.0,tmp);            //10^[log10（x）]==x
ans1=(ll)(tmp*100);            //x*100整数部分为3位

题目：UVA-11029-Leading and Trailing      UVa - 10692 - Huge Mods

 

 

唯一分解定理：

任意一个整数中可以写成x=(p1^a1)*(p2^a2).......(pi^ai) ,ai为一系列素数

这是解数论题时经常利用的一个性质，有题目：UVA 10791 Minimum Sum LCM  UVA 10539 Almost Prime Numbers

http://blog.csdn.net/sdau20163942/article/details/78450887

 

 

中国剩余定理：

牵扯到同余等等概念，所以其求解会用到下面的扩展欧几里得，是求解一次同余式组的方法，其定义如下

设正整数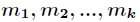两两互素，则同余方程组

 

                             

 

有整数解。并且在模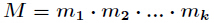下的解是唯一的，解为

 

                               

 

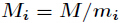
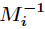
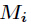
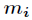
其中，而为模的逆元。

典型应用的题目有：poj-1006-Biorhythms

 

 

欧几里得与扩展欧几里得

扩展欧几里得是用来求ax+by=c的解，且如果c%gcd(a,b)!=0,则误解，用解出的（x0，y0）可以得到解系（x0+k*b',y0+ka'）,a'=a/gcd(a,b),b'=b/gcd(a,b);

 

int gcd(int a,int b)
{
    return b==0?a:gcd(b,a%b);
}

void extend_Euclide(ll a,ll b,ll &x,ll &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return;
    }
    extend_Euclide(b,a%b,x,y);
    int temp=x;
    x=y;
    y=temp-(a/b)*y;
}

 

 

void extend_Euclide(ll a,ll b,ll &d,ll &x,ll &y)
{
    if(b==0)
    {
        d=a;
        x=1;
        y=0;
        return;
    }
    extend_Euclide(b,a%b,d,y,x);
    y-=x*(a/b);
}

 

 

 

 

 

 

 

经常用到的比较优化的筛素数

 

void init()  
{  
    int m=sqrt(1000000+0.5);  
    int i,j;  
    c=0;  
    for(i=2;i<=m;i++)  
    {  
        if(!vis[i])  
        {  
            for(j=i*i;j<=1000000;j+=i)  
            {  
                vis[j]=true;  
            }  
        }  
    }
    for(i=2;i<=1000000;i++)  
    {  
        if(!vis[i])  
            prime[c++]=(ll)i;  
    }  
}

 

 

 

欧拉函数
求对于正整数n求小于n且与n互质的数的个数

 

ll euler_phi(ll n) //较快
{
    ll ans=n;
    for(ll i=2;i*i<=n;i++)
    if(n%i==0)
    {
        ans-=ans/i;
        while(n%i==0)
            n/=i;
    }
    if(n>1)
        ans-=ans/n;;
    return  ans;
}

 

 

 

 

 

 

int euler_phi(int n)  
{  
    int m=(int)sqrt(n+0.5);  
    int ans=n;  
    for(int i=2;i<=m;i++)  
    {  
        if(n%i==0)  
        {  
            ans=ans/i*(i-1);  
            while(n%i==0)  
                n/=i;  
        }  
    }  
    if(n>1)  
        ans=ans/n*(n-1);  
    return ans;  
}  

还可以直接求出所有的欧拉函数值

 

 

int phi[M];  
void init() //预先求出所有的欧拉函数  
{  
    int i,j;  
    for(i=2;i<M;i++)  
        phi[i]=0;  
    phi[1]=1;  
    for(i=2;i<M;i++)  
        if(!phi[i])  
    {  
        for(j=i;j<M;j+=i)  
        {  
            if(!phi[j])  
                phi[j]=j;  
            phi[j]=phi[j]/i*(i-1);  
        }  
    }  
}  

 

题目：UVa - 10692 - Huge Mods UVA - 10820 - Send a Table  uva-10299-Relatives

 

在数论中，欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则:

                                  a^(φ（n）)=1 （mod n）


其余内容以后再补充