B-树

B树

    它是多叉平衡树。

      我们知道二叉搜索树、平衡二叉树、红黑树都是动态查找树，典型的二叉搜索树结构，查找的时间复杂度和树的高度相关为O（log2N）。

       当我们查找时数据时一般可分为如下三情况：

             数据无序     ----->     线性搜索 O(n)

             有数数据     ----->     二分查找 O(log2n)

             二分搜索树 ----->    O(log2n)   （在最坏情况中为O(n)）

             AVL/红黑树  ----->   O(log2n)

         但是当我们用搜索树保存数据，搜索数据时，如果数据过多导致树高过高从而导致搜索效率降低。所以我们就引入了多叉搜索树，从而极大的降低树高来提高搜索效率。

B树定义

      7.有m个关键字必有m+1个节点由下面的分裂大家可以看出。

B树高度与查找速度

高度

h <= log┌m/2┐ (n+1)/2 

O(  log┌m/2┐ (n+1)/2  * m)

证明：

在高度为h的情况下，root至少有1个关键字与2个子节点。非root的情况下每个节点至少2/m个子节点与

2/m-1个关键字。那么节点个数推导如下

第一层  1 

第二层  2 

第三次 (2/m)*2

第四层 (2/m)^2 * 2

第h层  (2/m)^h-2  *2

                                                                                                  m/2^(h-1)-1

合并  1+2*{1+ (2/m) +(2/m)^2+...+(2/m)^(h-2)) }  = 1 + 2*(  --------------) = x 

                                                                                                      m/2 -1

又因为每个节点有 2/m-1个关键字，故一共有  

      (2/m-1)*x =  1+ 2*(m/2^(h-1) -1 )

设B树共有 N个关键字则h为

N >=  2*{m/2^(h-1)} -1 

h <= log┌m/2┐ (N+1)/2

查找

高度乘以每一次对应节点遍历其key数组的个数 。

O(  log┌m/2┐ (n+1)/2  * m)

B树规则

    由上述定义我们知道，当在一个节点中把关键字插满时，就需要做出改变，否则就违反B树性质，所以我们一般都是对其分裂，在关键字集合中，找到最中间的关键字，第一步把它右边的所以关键字移入新节点中，并把相应关键字对应的子节点也移入新节点中，第二步再把最中间的关键字提到父节点的关键字集合中。

     对应的图解如下：

     

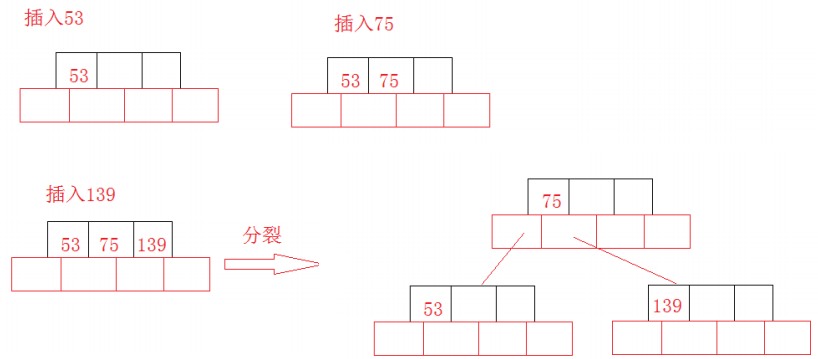
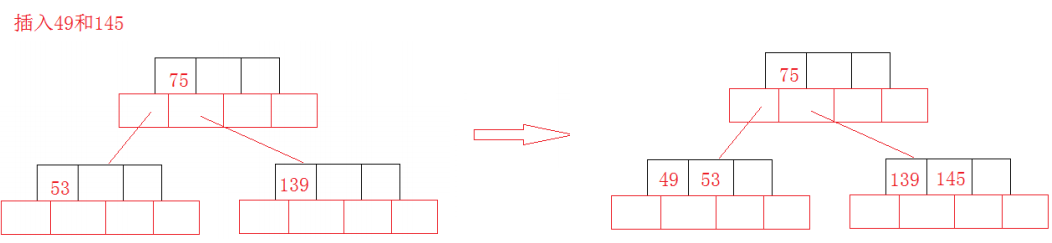
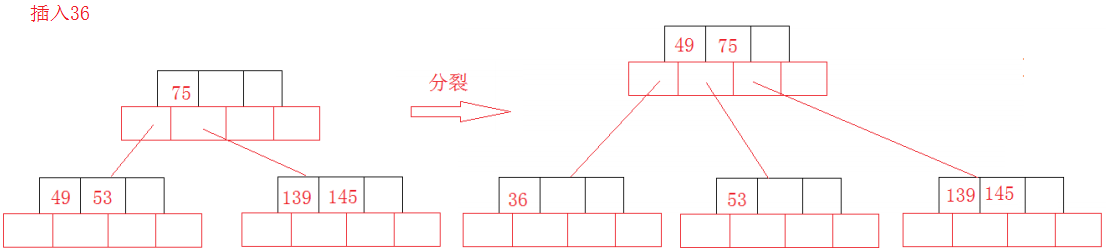
B树优缺点

优点

1.树高很低。（所以我们用在数据库引擎中可以减少I/O次数）

2.它是完全平衡的多叉树

3.查找效率可观

缺点

1.空间利用率低，非根节点，只能利用 [m/2,m) 之间。

2.查找效率相比红黑树相较更低。红黑树log2n ,及时10亿数据才比较30次。B树如果10亿数据，为了降低高度

我们会增加度数。当度数为100，树高大概都4~5层了(根算第一层)。那么它要比较 4*50=200次，效率明显不如

红黑树了。

B树代码

   

#include <iostream>
using namespace std;
template<class K, size_t M>
struct BTreeNode
{
	//K _keys[M-1];     // 关键字的集合
	//BTreeNode<K, M> _pSub[M];    // 孩子的集合

	// 多给一个关键字：为简化分裂的逻辑
	K _keys[M];     // 关键字的集合
	BTreeNode<K, M>* _pSub[M + 1];    // 孩子的集合
	BTreeNode<K, M>* _pParent;
	size_t _size; // 有效关键字的个数

	BTreeNode()
		: _size(0)
		, _pParent(NULL)
	{
		for (size_t idx = 0; idx < M + 1; ++idx)
			_pSub[idx] = NULL;

	}
};


template<class K, size_t M>
class BTree
{
	typedef BTreeNode<K, M> Node;
public:
	BTree()
		: _pRoot(NULL)
	{}

	pair<Node*, int> Find(const K& key)  //Node为 parent 
	{
		if (_pRoot == NULL)
		{
			return pair<Node*, int>((Node*)NULL, -1);
		}
		else
		{
			Node*pCur = _pRoot;
			Node*parent = NULL;
			while (pCur)
			{
				size_t idx = 0;;
				for (idx = 0; idx < pCur->_size; idx++)
				{
					if (key < pCur->_keys[idx])
					{
						break;
					}
					if (key == pCur->_keys[idx])
					{
						return pair<Node*, int>(pCur, idx);
					}
				}
				parent = pCur;
				pCur = pCur->_pSub[idx];
			}
			return pair<Node*, int>(parent, -1);
		}
	}
	bool Insert(const K& key)
	{
		if (_pRoot == NULL)
		{
			_pRoot = new Node;
			_pRoot->_keys[0] = key;
			_pRoot->_size++;
			//_InsertKey(_pRoot, key, NULL);
			return true;
		}
		pair<Node*, int> ret = Find(key);
		Node * pCur = ret.first;
		int  ICur = ret.second;
		if (ICur > 0) return false;  //节点已存在
		Node *pSub = NULL;
		Node * NewNode = NULL;
		size_t mid = 0;
		K _key = key;
		while (1)
		{
			mid = pCur->_size >> 1;
			_InsertKey(pCur, _key, pSub);
			if (pCur->_size < M)
			{
				return true;
			}
			else  
			{
				NewNode = new Node;
				for (size_t idx = mid + 1; idx < pCur->_size; idx++) //处理mid 右边的值
				{
					NewNode->_keys[NewNode->_size] = pCur->_keys[idx];
					NewNode->_pSub[NewNode->_size++] = pCur->_pSub[idx];
					if (pCur->_pSub[idx])
					{
						pCur->_pSub[idx]->_pParent = NewNode;
					}
				}
				NewNode->_pSub[NewNode->_size] = pCur->_pSub[pCur->_size];
				if (pCur->_pSub[pCur->_size])
				{
					pCur->_pSub[pCur->_size]->_pParent = NewNode;
				}
				pCur->_size = pCur->_size - NewNode->_size - 1;
				if (pCur->_pParent == NULL) // 处理上移的mid 当pCur为根时
				{
					Node*pRoot = new Node;
					pRoot->_keys[0] = pCur->_keys[mid];
					pRoot->_pSub[0] = pCur;
					pRoot->_pSub[1] = NewNode;
					NewNode->_pParent = pRoot;
					pCur->_pParent = pRoot;
					pRoot->_size++;
					_pRoot = pRoot;
					return true;
				}
				else
				{
					pSub = NewNode;
					_key = pCur->_keys[mid];
					pCur = pCur->_pParent;
				}
			}
		}
	}
	void InOrder()
	{
		cout << " InOrder:";
		_InOrder(_pRoot);
		cout << endl;
	}

private:
	void _InOrder(Node* pRoot)
	{
		if (pRoot)
		{
			for (size_t idx = 0; idx < pRoot->_size; idx++)
			{
				_InOrder(pRoot->_pSub[idx]);
				cout << pRoot->_keys[idx]<<"  ";
			}
			_InOrder(pRoot->_pSub[pRoot->_size]);
		}
	}
	void _InsertKey(Node* pCur, const K& key, Node* pSub)
	{
		size_t end = pCur->_size-1;
		for (int idx = end; idx >= 0; idx--)
		{
			if (key < pCur->_keys[idx])
			{
				pCur->_keys[idx+1] = pCur->_keys[idx];
				pCur->_pSub[idx+ 2] = pCur->_pSub[idx + 1];
			}
			else
			{
				pCur->_keys[idx + 1] = key;
				pCur->_pSub[idx+2] = pSub;  // [idx+1+1] 因为每个idx对应的指针域都为 idx+1 
				if (pSub) pSub->_pParent = pCur;
				break;
			}
			//if (pSub) pSub->_pParent = pCur;
		}
		pCur->_size++;
	}

private:
	Node* _pRoot;
};


void TestBTree()
{
	BTree<int, 3> t;
	t.Insert(10);
	t.Insert(30);
	t.Insert(20);
	t.Insert(40);
	t.Insert(50);
	t.Insert(38);
	t.Insert(35);
	t.InOrder();
}
int main()
{
	TestBTree();
	return 0;
}

      

又因为每个节点有 2/m