目录
1.递归实现:
1.递归实现:
1、二叉检索树的定义
对于查找问题,可分为静态查找与动态查找,静态查找即二分查找,对于给定的有序数组,不会再增加或删去元素;而动态查找则会在给定数组中增加或删减元素。对于动态查找,则需要使用二叉检索树。
二叉检索树(BST,Binary Search Tree),也称二叉排序树或二叉查找树。
一棵二叉树,可以为空;如果不为空,其根节点的关键之为k,且满足以下性质:
1. 非空左子树的所有键值小于其根结点的关键值k。
2. 非空右子树的所有键值等于其根结点的关键值k。
3. 左、右子树都是二叉搜索树。
2、二叉检索树结点的定义
链式二叉树的结点类,此处采用key-value模型:对于每一个key值都有与之对应的唯一的value值,即key,value是配对出现的。
这种做法在生活中也有类似的应用,例如:查找中英文字典时候,单词和其中文翻译就构成一种成对的结构;再比如统计某些情况单词字符的出现次数,也可以使用该模型。
public class BSTNode<Key extends Comparable<Key>, Value> { //泛型继承接口用的extends而不是 implements
private Key key;
private Value value;
private BSTNode<Key, Value> left;
private BSTNode<Key, Value> right;
//constructor部分
public BSTNode(Key key, Value value,BSTNode<Key, Value> left,BSTNode<Key, Value> right){
this.key=key;
this.value=value;
this.left=left;
this.right=right;
}
public boolean isLeaf() {
return left == null && right == null;
}
//getter与setter部分
public Key getKey() {
return key;
}
public void setKey(Key key) {
this.key = key;
}
public Value getValue() {
return value;
}
public void setValue(Value value) {
this.value = value;
}
public BSTNode<Key, Value> getLeft() {
return left;
}
public void setLeft(BSTNode<Key, Value> left) {
this.left = left;
}
public BSTNode<Key, Value> getRight() {
return right;
}
public void setRight(BSTNode<Key, Value> right) {
this.right = right;
}
}3、二叉检索树的实现
(1)查找
查找步骤:
查找从根结点开始
若树为空,返回NULL:没有找到要匹配的元素
若树非空,则将根结点关键字和要查找的元素的key值进行比较,并进行不同处理:
- 若要查找的元素的key值=根结点的key值,找到匹配元素,返回指向此结点的value值
- 若要查找的元素的key值<根结点key值,只需在左子树中继续搜索;
- 若要查找的元素的key值>根结点的key值,在右子树中进行继续搜索;
-
递归实现:
public Value find(Key key) {
try {
if (key == null)
throw new Exception("key is null");
} catch (Exception e) {
e.printStackTrace();
return null;
}
return findHelp(root, key);//调用findHelp,从root开始,把根结点传入参数root(指定的某树root)
}
private Value findHelp(BSTNode<Key, Value> rt, Key key) {
if (rt == null) return null;//查找失败,基准情形1
if(key.compareTo(rt.getKey())==0)
return rt.getValue();//找到值,基准情形2
else{
if (key.compareTo(rt.getKey()) < 0)
return findHelp(rt.getLeft(), key);//小于当前key值则往左子树查找
else
return findHelp(rt.getRight(), key);//大于当前key值则往右子树查找
}
}-
非递归实现:可将“尾递归”函数改为迭代函数
public Value find(Key key) {
try {
if (key == null)
throw new Exception("key is null");
} catch (Exception e) {
e.printStackTrace();
return null;
}
BSTNode<Key, Value> rootTemp = root;//需要用存下当前指向的结点,不能直接对root修改!
while(rootTemp!=null){
if(key.compareTo(rootTemp.getKey()) == 0)
return rootTemp.getValue();
else{
if(key.compareTo(rootTemp.getKey()) < 0)
rootTemp=rootTemp.getLeft();
else
rootTemp=rootTemp.getRight();
}
}
return null;//查找失败
}(2)查找与删除最小/最大元素

- 最大元素一定是在树的最右分枝的端结点上
- 最小元素一定是在树的最左分枝的端结点上
下文以最小元素为例说明该思想。
-
查找:
思想:
从根结点开始找,由于最小元素一定是在树的最左分枝的端结点上,因此一直向左走,直到当前结点的左子结点为空,当前结点元素即为最小元素,返回该结点。
代码实现:
1️⃣递归实现
public BSTNode getMinNode() {
if(rt == null)
return null;//空的二叉搜索树,返回null
else
return (getMinNodeHelp(root));//调用getMinNodeHelp,从root开始,把根结点传入参数root(指定的某树root)
}
private BSTNode getMinNodeHelp(BSTNode<Key, Value> rt) {
//最小元素一定是在树的最左分枝的端结点上,因此一直向左走,直到左子结点为空
if (rt.getLeft() == null)
return rt;//找到最左叶结点并返回
else
return getMinNodeHelp(rt.getLeft());//沿左分支继续查找
}2️⃣非递归实现
public BSTNode getMinNodeWithoutR(){
if(root == null)
return null;//空的二叉搜索树,返回null
BSTNode<Key, Value> rootTemp = root;//需要用存下当前指向的结点,不能直接对root修改!
while(rootTemp.getLeft()!=null)
rootTemp=rootTemp.getLeft();//沿左分支继续查找
return rootTemp;//找到最左叶结点,退出循环,并返回
}-
删除
思路:
- 从给定结点开始,一路向左找最小结点,直至当前结点无左子节点(基准情形)
- 将当前结点父结点的左子结点置为当前结点的右子结点
分析:
找到最小结点时,还需要对该位置的父结点的左子结点进行修改,因此,需要记忆父结点的位置。
同时需要考虑若最小结点在给定结点的位置时如何处理!1️⃣采用递归实现:
在非基准情形时做递归调用,期望子递归返回左子树在删除最小结点后的新树的根结点,将返回的根结点作为当前结点的左子结点。
可以注意到,修改子结点的操作仅对于最小结点的父结点有实际作用,对于上层结点并未修改其左子结点。由于使用递归操作的简便性,该操作冗余在可接受范围内。
2️⃣ 采用非递归实现:
分析:对于给定的结点分2种情况:
1.该结点就是根结点,此时parent=null。再分两种情况:1.没有左分支,故要删根结点,直接做root=root.getRight();
2.有左分支,与非根节点的操作相同,只需要依次遍历下去找最小结点即可;
2.非根结点,再分两种情况:1.该结点没有左分支,故要删该点,需要知道该结点的父结点;
2.该结点有左分支,无需知道该结点的parent,只需要依次遍历下去找最小结点即可。
步骤:因此,根据分析的情况可以将根结点+有左分支的情况与非根结点+有左分支的情况合并,算法步骤如下:
判断给定结点有无左分支,
1.若没有左分支则找该结点的父结点。根据父结点属性做如下操作:
1.若得到的父节点为null,表明给定结点为根结点,直接删除根结点即可;
2.若父结点存在,则将父节点的某子结点(根据查找时的方向)置为待删除结点的右节点。
2.若存在左分支,以给定结点出发,一路向左找最小值,并记录当前结点的父结点,直到当前遍历的结点无左分支,退出循环。再将当前的父结点的左子节点置为当前结点的右子结点。
返回当前结点。

1️⃣递归实现
private BSTNode<Key, Value> deleteMinNode(BSTNode<Key, Value> current) {
//递归写法,对于在给定结点为最小时需要修改父结点的操作,感觉不是很好,此写法参考非递归思路更清晰
if (current.getLeft() == null) {
BSTNode<Key, Value> rootTemp = root;
BSTNode<Key, Value> parent = null;
while (rootTemp != current) {
parent = rootTemp;
if (current.getKey().compareTo(rootTemp.getKey()) < 0)
rootTemp = rootTemp.getLeft();
else
rootTemp = rootTemp.getRight();
}
if (parent == null)
root = root.getRight();//若删除的是根结点
else {//非根节点
if (current.getKey().compareTo(parent.getKey()) < 0)
parent.setLeft(current.getRight());
else
parent.setRight(current.getRight());
}
return current.getRight();//返回给定子树更新以后的根结点
} else {
return deleteMinNodeR(current);//调用递归函数
}
}
private BSTNode<Key, Value> deleteMinNodeR(BSTNode<Key, Value> rt){
if (rt.getLeft() == null)
rt = rt.getRight();
else
rt.setLeft(deleteMinNode(rt.getLeft()));//冗余操作是可以接受的
return rt;
}2️⃣非递归实现
public BSTNode deleteMinNodeWithoutR(BSTNode<Key, Value> rt) {
//删除该结点下的最小结点,返回给定子树更新以后的根结点
BSTNode<Key, Value> current = rt;
BSTNode<Key, Value> parent;
if (current.getLeft() == null) {//若给定结点即为该树的最小结点,找其父结点
BSTNode<Key, Value> rootTemp = root;
parent = null;
while (rootTemp != current) {
parent = rootTemp;
if (current.getKey().compareTo(rootTemp.getKey()) < 0)
rootTemp = rootTemp.getLeft();
else
rootTemp = rootTemp.getRight();
}
if (parent == null)
root = root.getRight();//若删除的是根结点
else {
if (current.getKey().compareTo(parent.getKey()) < 0)
parent.setLeft(current.getRight());
else
parent.setRight(current.getRight());
}
return current.getRight();//返回给定子树更新以后的根结点
} else {
BSTNode<Key, Value> res=current;//临时保存cur的值,返回给定子树更新以后的根结点
while (current.getLeft() != null) {
parent = current;
current = current.getLeft();
}
parent.setLeft(current.getRight());
return res;
}
}同理,对于最大元素操作代码实现如下
public BSTNode getMaxNode() {
if(root == null)
return null;//空的二叉搜索树,返回null
else
return (getMaxNodeHelp(root));
}
private BSTNode getMaxNodeHelp(BSTNode<Key, Value> rt) {
if (rt.getRight() == null)
return rt;
else
return getMaxNodeHelp(rt.getRight());
}
private BSTNode<Key, Value> deleteMaxNode(BSTNode<Key, Value> rt) {
//此处为在给定结点为最大时,未修改父结点的代码
if (rt.getRight() == null)
rt = rt.getLeft();
else
rt.setRight(deleteMaxNode(rt.getRight()));
return rt;
}(3)插入元素
思路:
- 找应插入的位置(类似于find方法),即所属位置父结点的空子结点。
- 找到后用key值与value值创建结点(该结点无左右子树),返回一个结点的二叉搜索树
- 修改上一层父结点的某子结点
分析:
找到插入位置时,还需要对该位置的父结点的某子结点进行修改,因此,需要记忆父结点的位置
1️⃣采用递归实现:
在非基准情形时做递归调用,期望子递归返回子树在插入待插结点后的新树的根结点,将返回的根结点作为当前结点的某子结点(与调用时方向相同)可以注意到,修改子结点的操作仅对于插入位置的父结点有实际作用,对于上层结点并未修改其子结点值。由于使用递归操作的简便性,该操作冗余在可接受范围内。
2️⃣ 采用非递归实现:
若为空子树,直接插入当前元素作为根结点,退出。若为非空子树,需要设置parent与current指针,记录遍历到的父结点,寻找待插入位置:
1. 若存在相同key值的结点,则只需要更新value值,无需修改任何结点的子结点,退出即可。
2. 若不存在相同key值的结点,则继续找待插入位置,根据待插入结点的key值与当前current的key值的关系,确定向左向右查找,修改parent与current指针,直至找到待插入位置,此时current为null,退出循环。
退出循环后,在current位置生成一个结点的二叉搜索树。
修改父结点的某子结点,将current所在位置的二叉树设为parent的子结点,通过key值大小判断左右。

1️⃣ 递归实现:
public void insert(Key key, Value value) {
try { //检查传入的结点属性是否合法
if (key == null) throw new Exception("Key is null, insert fault!");
if (value == null) throw new Exception("Value is null, insert fault!.");
} catch (Exception e) {
e.printStackTrace();
}
调用insertHelp,从root开始,把根结点传入参数root(指定的某树root)
root = insertHelp(root, key, value);
}
private BSTNode<Key, Value> insertHelp(BSTNode<Key, Value> rt, Key key, Value value) {
//找到插入位置,生成并返回一个结点的二叉搜索树,作为上一层的子结点。基准情形1
if (rt == null)
return new BSTNode<Key, Value>(key, value, null, null);
//否则继续找要插入元素的位置
if (key.compareTo(rt.getKey()) < 0)
rt.setLeft(insertHelp(rt.getLeft(), key, value));
else if (key.compareTo(rt.getKey()) > 0)
rt.setRight(insertHelp(rt.getRight(), key, value));
else
rt.setValue(value);//如果key值相同则更新value值。基准情形2
return rt;
}2️⃣ 非递归实现:
public void insert(Key key, Value value) {
if (root == null) {
root = new BSTNode<Key, Value>(key, value, null, null);
return;//空子树,直接插入,退出
}
BSTNode<Key, Value> parent = null;
BSTNode<Key, Value> current = root;
while (current != null) {
if (key.compareTo(current.getKey()) == 0) {
current.setValue(value);
return;//如果key值相同则更新value值,无需修改任何结点的子结点,退出
} else {//继续找待插入位置
if (key.compareTo(current.getKey()) < 0) {
parent = current;
current = current.getLeft();
} else {
parent = current;
current = current.getRight();
}
}
}
//退出循环表示已经找到待插入位置,在current位置生成一个结点的二叉搜索树
current = new BSTNode<Key, Value>(key,value,null,null);
//修改父结点的某子结点,通过key值大小判断左右
if(key.compareTo(parent.getKey()) < 0)
parent.setLeft(current);
else
parent.setRight(current);
} 不同的插入顺序会生成不同的二叉树。
应尽可能保证二叉树的平衡性:任意结点的左右子树的高度之差( ,记为平衡因子BF,Balance Factor)的绝对值小于等于1,则说明这棵树是平衡的,称这种树为平衡二叉树(AVL树)。
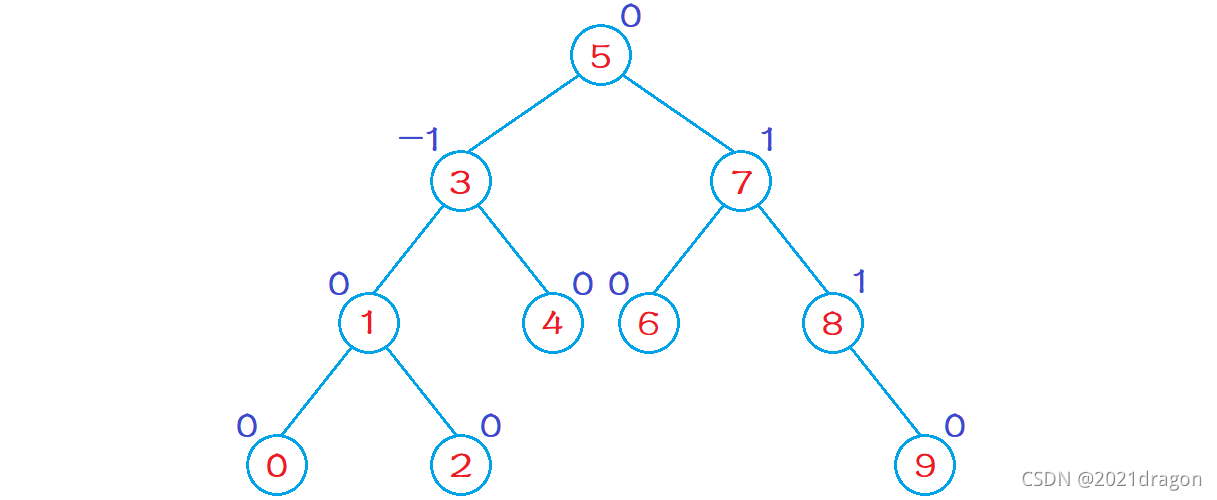
对于AVL树,有以下性质:给定结点数为n的AVL树的最大高度为ceil()。
(4)删除结点
分析:考虑三种情况:
1. 要删除的是叶结点:直接删除,并再修改其父结点的子结点(置为 null)
2. 要删除的结点只有一个孩子结点: 将其父结点的指针指向要删除结点的孩子结点
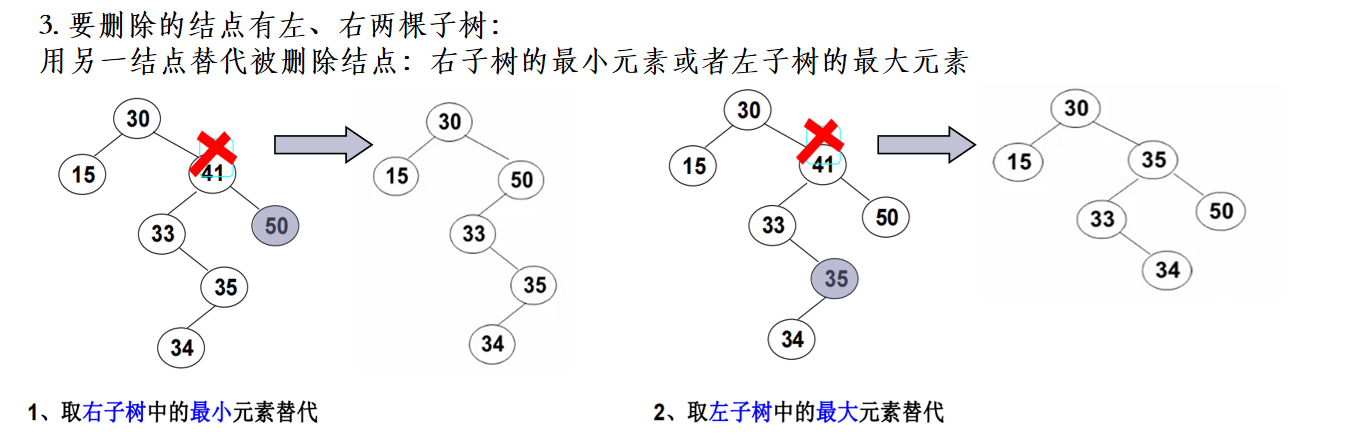
3. 要删除的结点有左、右两棵子树(包含了是根结点的情况,需要小心处理):用另一结点替代被删除结点:右子树的最小元素或者左子树的最大元素
找最接近待删除结点key值的结点,使得需要变化的结点数目最少。
由于待删除结点的左子树中所有结点的key值<待删除结点的key值<=待删除结点的右子树中所有结点的key值,可得到关系式:
待删除结点的左子树中所有结点的key值<=左子树中最大结点key值<待删除结点的key值<=右子树中最小结点key值<=待删除结点的右子树中所有结点的key值
故,找左子树上最大值/右子树上最小值结点,即可用于替代待删除的结点。由于左子树上最大值/右子树上最小值结点必定没有两个子结点,故替换后该问题转换为删除最小最大结点的问题
在存在重复值的问题中(重复值只能挂在右子树中),采用选择右子树的最小值替换更为合理。


步骤:
先找到要删除的结点。若当前结点为null,则表示不存在待删除元素,则返回null;否则继续向下查找
找到待删除元素后,根据该结点的度进行不同的处理:
1.若待删除结点不存在左子节点/右子节点:直接将右子结点/左子结点作为当前根结点
2.待删除结点有两个子结点:将当前结点的key和value更新为右子树中的最小结点的值,并将当前结点的右子结点进行更新,即删除右子树中的最小结点1️⃣采用递归实现:
将问题转化为删除右子树最小结点后,返回待删除结点删除后的二叉树的根结点,将返回的根结点作为当前结点的某子结点(与调用时方向相同),一直返回到根结点处。
故此时同样适用于删除根结点的操作,无需分类讨论修改根结点。
(该操作同插入操作存在可接受的冗余)
2️⃣ 采用非递归实现:
使用parent与current指针记录当前位置的父结点与结点,分2种情况讨论:
1.待删除结点为根结点时,对子结点个数不同情况做具体操作。
2.待删除结点非根节点时,对子结点个数不同情况做具体操作。
由于deleteHelp() 函数中已经有查找待删除结点的步骤,可记录其父结点,故若待删除结点的右子树中的最小值是该右子树的根结点时,在deleteMinNode()函数中无需修改其父结点的子结点值(常规操作中需要从根结点遍历到该结点的父结点),只需在deleteHelp() 函数中直接修改待删除结点的右子结点为deleteMinNode()函数的返回值(给定子树更新以后的根结点)即可。故对上述的deleteMinNode()函数做如下变式:
递归实现:
private BSTNode<Key, Value> deleteMinNode(BSTNode<Key, Value> rt) { //返回给定子树更新以后的根结点 if (rt.getLeft() == null) rt = rt.getRight(); else rt.setLeft(deleteMinNode(rt.getLeft()));//冗余操作是可以接受的 return rt; }非递归实现:
public BSTNode<Key, Value> deleteMinNode(BSTNode<Key, Value> rt) { //返回给定子树更新以后的根结点 BSTNode<Key, Value> current = rt; if (current.getLeft() == null) return current.getRight();//给定结点为最小结点,直接返回给定结点的右子结点即可 //若给定结点非最小结点 BSTNode<Key, Value> parent; BSTNode<Key, Value> res = current;//临时保存cur的值,返回给定子树更新以后的根结点 do { parent = current; current = current.getLeft(); } while (current.getLeft() != null); parent.setLeft(current.getRight()); return res; }
private BSTNode getMinNodeHelp(BSTNode<Key, Value> rt) {
if (rt.getLeft() == null)
return rt;//找到最左叶结点并返回
else
return getMinNodeHelp(rt.getLeft());//沿左分支继续查找
}1️⃣递归实现:
private Value removeValue;
public Value delete(Key key) {
removeValue = null;
try {
if (key == null)
throw new Exception("Key is null, delete failure");
} catch (Exception e) {
e.printStackTrace();
return null;
}
//调用deleteHelp,从root开始,把根结点传入参数root(指定的某树root)
root = deleteHelp(root, key);
return removeValue;
}
private BSTNode<Key, Value> deleteHelp(BSTNode<Key, Value> rt, Key key) {
//返回该层递归生成的新子树的根结点
if (rt == null) {
System.out.println("No Such key");//没找到待删除元素
return null;
}
if(key.compareTo(rt.getKey()) == 0){//找到待删除元素了
removeValue = rt.getValue();
if (rt.getLeft() == null)
rt = rt.getRight();//左子结点为空,直接将右子结点作为当前根结点
else if (rt.getRight() == null)
rt = rt.getLeft();//右子结点为空,直接将左子结点作为当前根结点
else {//待删除结点有两个子结点
rt.setKey((Key) getMinNodeHelp(rt.getRight()).getKey());
rt.setValue((Value) getMinNodeHelp(rt.getRight()).getValue());
//将当前结点的key和value更新为右子树中的最小结点的值
rt.setRight(deleteMinNode(rt.getRight()));
//将当前结点的右子结点进行更新,即删除右子树中的最小结点
}
}else{//继续找待删除元素
if (key.compareTo(rt.getKey()) < 0)
rt.setLeft(deleteHelp(rt.getLeft(), key));
else
rt.setRight(deleteHelp(rt.getRight(), key));
}
return rt;
}2️⃣ 非递归实现:
public Value deleteWithoutR(Key key) {
BSTNode<Key, Value> parent = null;
BSTNode<Key, Value> current = root;
while (current != null) {
if (key.compareTo(current.getKey()) == 0) {//找到待删除元素了
Value removeValue = current.getValue();
if (parent == null) {//等价于root == current,待删除的是根结点
if (root.getLeft() == null)
root = root.getRight();//根结点的左子结点为空,直接将右子结点作为当前根结点
else if (current.getRight() == null)
root = root.getLeft();//根结点右子结点为空,直接将左子结点作为当前根结点
else {//根结点有两个子结点
root.setKey((Key) getMinNodeHelp(root.getRight()).getKey());
root.setValue((Value) getMinNodeHelp(root.getRight()).getValue());
//将当前结点的key和value更新为右子树中的最小结点的值
root.setRight(deleteMinNode(root.getRight()));
//将当前结点的右子结点进行更新,即删除右子树中的最小结点
}
} else {
if (current.getLeft() == null) {//左子结点为空,直接将右子结点作为当前根结点
if (current.getKey().compareTo(parent.getKey()) < 0)
parent.setLeft(current.getRight());
else
parent.setRight(current.getRight());
} else if (current.getRight() == null) {//右子结点为空,直接将左子结点作为当前根结点
if (current.getKey().compareTo(parent.getKey()) < 0)
parent.setLeft(current.getLeft());
else
parent.setRight(current.getLeft());
} else {//待删除结点有两个子结点
current.setKey((Key) getMinNodeHelp(current.getRight()).getKey());
current.setValue((Value) getMinNodeHelp(current.getRight()).getValue());
//将当前结点的key和value更新为右子树中的最小结点的值
current.setRight(deleteMinNode(current.getRight()));
//将当前结点的右子结点进行更新,即删除右子树中的最小结点
if (current.getKey().compareTo(parent.getKey()) < 0)
parent.setLeft(current);
else
parent.setRight(current);
//更新父结点的某子结点
}
}
return removeValue;
} else {//继续找待删除元素
if (key.compareTo(current.getKey()) < 0) {
parent = current;
current = current.getLeft();
} else {
parent = current;
current = current.getRight();
}
}
}
System.out.println("No Such key");
return null;
}4、操作的时间代价分析
1.搜索、插入、删除的时间代价:
● 平衡二叉树的操作代价为O(logn)
● 非平衡的二又树最差的代价为O(n)
2.周游一个二叉树的代价为O(n)
使一个二叉树保持平衡才能真正发挥二叉树的作用,平衡的两种方法:
1. AVL平衡二叉树 (旋转)
2. 在对一组数据构建二叉树时先将数据随机打乱
5、AVL平衡二叉树
向AVL树插入结点或删除结点时可能会破坏树的平衡性,此时要调整树的结构,平衡化处理恢复平衡使之重新达到平衡且保持BST的结构性质,下文以插入操作为例分析。
用紫色方格表示新插入的结点,又称为“麻烦结点”,A表示离新插入结点最近的且平衡因子变为±2的祖先结点,又称为“发现者”。
在每插入/删除结点时均需要更新所有结点的BF值并判断当前结点是否平衡:新增结点在其父结点结点的右边,父结点BF值+1;否则-1。
依次往上更新,若当前结点的BF值为0则其上层结点必定平衡[分析:由于每次更新只会+1、-1或不操作,故对于该结点为根的树来说,插入或删除结点只会把空位填补或删除多余的结点,故趋于平衡,整体即平衡];
若该结点BF值为±1,有继续向上更新的必要;
若该结点BF值变为±2,则需要进行旋转处理。
因此,可以注意到,当平衡被破坏时,A结点在“麻烦结点”一侧子结点的BF值必定为±1,而不会为0。
因此,分析平衡打破的4种情况,可用4种旋转进行平衡化处理:
● LL型: 新结点被插入到 A 的左子树的左子树上,BF(curNode)=2,BF(curNode.left)=1→顺(左单旋)
● LR型:新结点被插入到 A 的左子树的右子树上,BF(curNode)=2,BF(curNode.left)=-1→先逆后顺(右左双旋)
● RR型:新结点被插入到 A 的右子树的右子树上,BF(curNode)=-2,BF(curNode.right)=-1 →逆(右单旋)
● RL型:新结点被插入到 A 的右子树的左子树上,BF(curNode)=-2,BF(curNode.right)=1 →先顺后逆(左右双旋)
1.LL型:
新结点被插入到 A 的左子树的左子树上,导致A结点的BF=A的左子树的高度-A的右子树的高度=2,且A的左子结点B的BF=1。
根据各结点的键值大小关系:B的左子树上所有结点<B<B的右子树上所有结点<A<A的右子树上所有结点
因此,可做下图所示的调整:以B结点为该树的根结点,构造[B的左子树] - B结点 - [ [B的右子树] - A结点 - [A的右子树] ]的结构。

此时可做顺时针旋转(左单旋):
先记录下当前根结点A的值(以原根结点的值创建新的结点);A新的左子结点为B结点的右子结点;右子树仍为A结点的右子树。
再将该树的根结点修改为B结点;新的左子树仍为B的左子树,一并旋转过去;新的右子结点为创建的新结点(修改后的A结点)。
注意!不可直接把传入的形参指向新的B结点!
(代码举例:rt=new AVLTNode(rt.left.key,rt.left.left,newNode))
如此操作只是把形参的指针指向了B结点,实际上不会修改传入的实参指向的结点内容。
2.LR型:
新结点被插入到 A 的左子树的右子树上(有两种可能的情形:①在C的左子树上,②在C的右子树上),导致A结点的BF=A的左子树的高度-A的右子树的高度=2,且A的左子结点B的BF=-1。
根据各结点的键值大小关系:B的左子树上所有结点<B<C的左子树上所有结点<C<C的右子树上所有结点<A<A的右子树上所有结点
因此,可做下图所示的调整:以C结点为该树的根结点,构造[ [B的左子树] - B结点 - [C的左子树] ] - C结点 - [ [C的右子树] - A结点 - [A的右子树] ]的结构。
此时可做先逆时针后顺时针的旋转(右左双旋),即先对B做逆时针旋转,后对A做顺时针旋转:
Step1.对B结点做逆时针旋转:对以B为根结点的树操作
先记录下当前根结点B的值(以原根结点的值创建新的结点);B左子树仍为B结点的左子树;新的右子结点为C结点的左子结点。
再将该树的根结点修改为C结点;新的左子结点为创建的新结点(修改后的B结点);新的右子树仍为C的右子树,一并旋转过去。
Step2.再对A结点做顺时针旋转:对以A为根结点的树操作
先记录下当前根结点A的值(以原根结点的值创建新的结点);A新的左子结点为C结点(A的新左子树)的右子结点;右子树仍为A结点的右子结点。
再将该树的根结点修改为C结点(A的新左子树的根结点);新的左子树仍为C的左子树,一并旋转过去;新的右子结点为创建的新结点(修改后的A结点)。
3.RR型:
新结点被插入到 A 的右子树的右子树上,导致A结点的BF=A的左子树的高度-A的右子树的高度=-2,且A的右子结点B的BF=-1。
根据各结点的键值大小关系:A的左子树上所有结点<A<B的左子树上所有结点<B<B的右子树上所有结点
因此,可做下图所示的调整:以B结点为该树的根结点,构造[ [A的左子树] - A结点 - [B的左子树] ] - B结点 - [B的右子树]的结构。
此时可做逆时针旋转(右单旋):
先记录下当前根结点A的值(以原根结点的值创建新的结点);A左子树仍为A结点的左子树;新的右子结点为B结点的左子结点。
再将该树的根结点修改为B结点;新的左子结点为创建的新结点(修改后的A结点);新的右子树仍为B的右子树,一并旋转过去。
4.RL型:
新结点被插入到 A 的右子树的左子树上(有两种可能的情形:①在C的左子树上,②在C的右子树上),导致A结点的BF=A的左子树的高度-A的右子树的高度=-2,且A的右子结点B的BF=1。
根据各结点的键值大小关系:A的左子树上所有结点<A<C的左子树上所有结点<C<C的右子树上所有结点<B<<B的右子树上所有结点
因此,可做下图所示的调整:以C结点为该树的根结点,构造[ [A的左子树] - A结点 - [C的左子树] ] - C结点 - [ [C的右子树] - B结点 - [B的右子树] ]的结构。
此时可做先顺时针后逆时针的旋转(左右双旋),即先对B做顺时针旋转,后对A做逆时针旋转:
Step1.对B结点做顺时针旋转:对以B为根结点的树操作
先记录下当前根结点B的值(以原根结点的值创建新的结点);B新的左子结点为C结点的右子结点;右子树仍为B结点的右子树。
再将该树的根结点修改为C结点;新的左子树仍为C的左子树,一并旋转过去;新的右子结点为创建的新结点(修改后的B结点)。
Step2.再对A结点做逆时针旋转:对以A为根结点的树操作
先记录下当前根结点A的值(以原根结点的值创建新的结点);A左子树仍为A结点的左子树;新的右子结点为C结点(A的新右子树的根结点)的左子结点。
再将该树的根结点修改为C结点(A的新右子树的根结点);新的左子结点为创建的新结点(修改后的A结点);新的右子树仍为C的右子树,一并旋转过去。
删除与插入操作是对称的(镜像,互逆的):
1.删除右子树结点导致失衡时,相当于在左子树插入导致失衡,即LL或LR;
2.删除左子树结点导致失衡时,相当于在右子树插入导致失衡,即RR或RL;
删除操作可能需要多次平衡化处理:由于平衡化不会增加子树的高度,但可能会减少子树的高度,所以在有可能使树增高的插入操作中,一次平衡化能抵消掉树增高;但在有可能使树减低的删除操作中,平衡化可能会带来祖先结点的不平衡。因此,删除操作可能需要多次平衡化处理。
源代码
● 结点的定义
public class AVLTNode {
int key;
AVLTNode left;
AVLTNode right;
public AVLTNode(int key,AVLTNode left,AVLTNode right) {
this.key = key;
this.left=left;
this.right=right;
}
public String toString() {
return "Node [key=" + key + "]";
}
}● 树的实现
public class AVLTree {
private AVLTNode root;
public AVLTNode getRoot() {
return root;
}
public void insert(int key) {
root = insertHelp(root, key);//调用insertHelp,从root开始,把根结点传入参数root(指定的某树root)
balanced(root);
}
private AVLTNode insertHelp(AVLTNode rt, int key) {
if (rt == null)
return new AVLTNode(key, null, null);//找到插入位置,生成并返回一个结点的二叉搜索树,作为上一层的子结点。基准情形1
//否则继续找要插入元素的位置
if (key < rt.key)
rt.left = insertHelp(rt.left, key);// 递归的向左子树添加
else if (key > rt.key)
rt.right = insertHelp(rt.right, key);// 递归的向右子树添加
//如果key值相同,无需操作。返回即可。基准情形2
balanced(rt);//添加结点之后做平衡调整
return rt;
}
public void delete(int key) {
//调用deleteHelp,从root开始,把根结点传入参数root(指定的某树root)
root = deleteHelp(root, key);
balanced(root);
}
private AVLTNode deleteHelp(AVLTNode rt, int key) {
//返回该层递归生成的新子树的根结点
if (rt == null) {
System.out.println("No Such key");//没找到待删除元素
return null;
}
if (key == rt.key) {//找到待删除元素了
if (rt.left == null)
rt = rt.right;//左子结点为空,直接将右子结点作为当前根结点
else if (rt.right == null)
rt = rt.left;//右子结点为空,直接将左子结点作为当前根结点
else {//待删除结点有两个子结点
rt.key = getMinNodeHelp(rt.right).key;
//将当前结点的key更新为右子树中的最小结点的值
rt.right = deleteMinNode(rt.right);
//将当前结点的右子结点进行更新,即删除右子树中的最小结点
}
} else {//继续找待删除元素
if (key < rt.key)
rt.left = deleteHelp(rt.left, key);
else
rt.right = deleteHelp(rt.right, key);
}
balanced(rt);
return rt;
}
private AVLTNode getMinNodeHelp(AVLTNode rt) {
//最小元素一定是在树的最左分枝的端结点上,因此一直向左走,直到左子结点为空
if (rt.left == null)
return rt;//找到最左叶结点并返回
else
return getMinNodeHelp(rt.left);//沿左分支继续查找
}
private AVLTNode deleteMinNode(AVLTNode rt) {
// 没有对父结点进行修改,和delete操作一起看是可以的
// 返回给定子树更新以后的根结点
if (rt.left == null)
rt = rt.right;
else
rt.left = deleteMinNode(rt.left);//冗余操作是可以接受的
return rt;
}
private void balanced(AVLTNode rt) {
//当添加或删除完一个结点后BF==2, 表明造成失衡是在当前结点的左侧,属于LL或LR的一种。
if (getBF(rt) >= 2) {
// 左子结点的BF值==1,则为LL型;左子结点的BF值==-1,为LR型
if (getBF(rt.left) >= 1) {//LL型
clockwiseRotate(rt);//直接对该结点进行顺时针旋转即可
} else {//LR型
counterclockwiseRotate(rt.left);//先对该结点的左子结点逆时针旋转
clockwiseRotate(rt);//再对该结点进行顺时针旋转
}
}
//当添加或删除完一个结点后BF==-2, 表明造成失衡是在当前结点的右侧,属于RR或RL的一种。
if (getBF(rt) <= -2) {
// 右子结点的BF值==1,则为RL型;右子结点的BF值==-1,为RR型
if (getBF(rt.right) >= 1) {//RL型
//rt.right != null && getHeight(rt.right.left) > getHeight(rt.right.right)这句有什么必要吗
clockwiseRotate(rt.right);//先对该结点的右子结点顺时针旋转
counterclockwiseRotate(rt); //再对该结点进行逆时针旋转
} else {//RR型
counterclockwiseRotate(rt);//直接对该结点进行逆时针旋转即可
}
}
}
private void counterclockwiseRotate(AVLTNode rt) {
//以原根结点的值创建新的结点,左子树不改变仍为原根结点的左子树,右子树修改为原根结点的右子结点(新根结点)的左子结点。
AVLTNode newNode = new AVLTNode(rt.key, rt.left, rt.right.left);
rt.key = rt.right.key; //新根结点为原根结点的右子结点
rt.left = newNode; //新根结点的左子结点为创建的新结点(键值为原根结点)
rt.right = rt.right.right; //新根结点的右子树仍为新根结点的右子树,一并旋转过去。
//不能写作rt=new AVLTNode(rt.right.key,rt.right.right,newNode)!rt是形参,此代码只是把形参的指针指向了B结点,实际上不会修改传入的实参指向的结点内容。
}
private void clockwiseRotate(AVLTNode rt) {
//以原根结点的值创建新的结点,左子树修改为原根结点的左子结点(新根结点)的右子结点,右子树不改变仍为原根结点的右子树。
AVLTNode newNode = new AVLTNode(rt.key, rt.left.right, rt.right);
rt.key = rt.left.key; //新根结点为原根结点的左子结点
rt.left = rt.left.left; //新根结点的左子树仍为新根结点的左子树,一并旋转过去。
rt.right = newNode; //新根结点的右子结点为创建的新结点(键值为原根结点)
//不能写作rt=new AVLTNode(rt.left.key,rt.left.left,newNode)!rt是形参,此代码只是把形参的指针指向了B结点,实际上不会修改传入的实参指向的结点内容。
}
public int getHeight(AVLTNode rt) {
// int height = 0;
// if (rt == null) return 0;
// height = Math.max(getHeight(rt.left), getHeight(rt.right)) + 1;
// return height;
if (rt==null) return 0;
return Math.max(rt.left == null ? 0 : getHeight(rt.left), rt.right == null ? 0 : getHeight(rt.right)) + 1;
}
public int getBF(AVLTNode rt) {
return getHeight(rt.left) - getHeight(rt.right);
}
void infixOrderByRecursion(AVLTNode root) {
if (root == null) return;//空树
infixOrderByRecursion(root.left);
System.out.println(root); //(访问)打印结点
infixOrderByRecursion(root.right);
}
}● 测试代码
public class TestAVLTree {
public static void main(String[] args) {
int[] arr = {25, 27, 30, 12, 11, 18, 14, 20, 15, 22};
//创建一个 AVLTree对象
AVLTree avlTree = new AVLTree();
for (int i = 0; i < arr.length; i++){
avlTree.insert(arr[i]);
}
//遍历
System.out.println("中序遍历");
avlTree.infixOrderByRecursion(avlTree.getRoot());
System.out.println("树的高度=" + avlTree.getHeight(avlTree.getRoot())); //3
System.out.println("树的左子树高度=" + avlTree.getHeight(avlTree.getRoot().left)); // 2
System.out.println("树的右子树高度=" + avlTree.getHeight(avlTree.getRoot().right)); // 2
System.out.println("当前的根结点=" + avlTree.getRoot());//8
avlTree.delete(100);//输出NoSuchKey
//遍历
System.out.println("中序遍历");
avlTree.infixOrderByRecursion(avlTree.getRoot());
System.out.println("树的高度=" + avlTree.getHeight(avlTree.getRoot())); //3
System.out.println("树的左子树高度=" + avlTree.getHeight(avlTree.getRoot().left)); // 2
System.out.println("树的右子树高度=" + avlTree.getHeight(avlTree.getRoot().right)); // 2
System.out.println("当前的根结点=" + avlTree.getRoot());//8
}
}6、红黑树(Red-Black Tree,RBT)
7、二叉检索树的应用举例
(1)判断某一序列是否生成同一棵二叉检索树
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。
例如,按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。
问题:对于输入的各种插入序列,需要判断它们是否能生成一样的二叉搜索树。
给出输入样例,第一行输入两个整数n和d,n表示树的结点个数,d表示待判断的序列个数。第二行输入基准的二叉检索树,后续d行输入需要和基准二叉树比较的序列。依次判断d个序列生成二叉检索树是否和基准序列相同。
例如:
4 2
3 1 4 2
3 4 1 2
3 2 4 1
思路:
解法1.不建树的判别方法:(使用递归的方式完成判断)
Step1 以第一个结点为基准结点,判断待比较的两序列基准节点是否相同,不同则表示生成的二叉检索树不同,返回;若相同则按照原序列顺序,将后续结点根据大于、小于基准结点分成两个子序列。
Step2 对于两个子序列,继续重复上一步,直到子序列中仅一个结点,返回。

解法2.建一棵树,再判别其他序列是否与该树一致
Step1 建树,树的参数有键值、左子结点、右子结点、判断是否被遍历过的flag标志
Step2 判别一序列是否与基准树一致
● 判别方法:在基准树中按顺序搜索待比较序列中的每个数
如果每次搜索所经过的结点在前面均出现过,则一致;
否则(某次搜索中遇到前面未出现的结点),则不一致,退出判断。
注意:在遍历下一序列时需要抹去基准树中被此次遍历的痕迹。
● 代码实现:构造judge方法,判断在搜索当前结点时所经过的结点是否在前面均出现过:
若遍历过当前结点(即该结点的flag为true),则值为key应该继续往下插入,判断key值与当前结点key值的关系
1.若相等,由于K型二叉检索树中不可能出现重复的结点,当前序列出错
2.若不相等,判断值为key的结点的插入方向
若当前结点没遍历过:要么是当前结点的插入位置,将该结点的flag置为true,要么是序列不同,返回false。
import java.util.Scanner;
public class BSTJudgeSame {
private class BSTNode {
int key;
BSTNode left;
BSTNode right;
boolean flag;
BSTNode(int key) {
this.key = key;
this.left = null;
this.right = null;
this.flag = false;
}
}
public static void main(String[] args) {
BSTJudgeSame bst = new BSTJudgeSame();
int n, d;
Scanner in = new Scanner(System.in);
do {
System.out.println("输入检索树结点数目:");
n = in.nextInt();
} while (n <= 0);
do {
System.out.println("输入需要与基准二叉树比较的二叉树序列数目:");
d = in.nextInt();
} while (d <= 0);
int[] baseNode = new int[n];
for (int i = 0; i < n; i++) {
baseNode[i] = in.nextInt();
}
BSTNode root = bst.makeTree(n, baseNode);
for (int i = 0; i < d; i++) {
int[] judgeNode = new int[n];
for (int j = 0; j < n; j++) {
judgeNode[j] = in.nextInt();
}
boolean isSame = true;
for (int j = 0; j < n && isSame; j++) {
if (!bst.judge(root, judgeNode[j])) isSame = false;
}
if (isSame)
System.out.println("is Same!");
else
System.out.println("not Same!");
bst.resetTree(root);//清除标记的flag
}
}
void preOrderByRecursion(BSTNode root) {
if (root == null) return;//空树
System.out.println(root.key);
preOrderByRecursion(root.left);
preOrderByRecursion(root.right);
}
private BSTNode makeTree(int nodeNum, int[] baseNode) {
BSTNode root = new BSTNode(baseNode[0]);
for (int i = 1; i < baseNode.length; i++) {
root = insert(root, baseNode[i]);
}
return root;
}
private BSTNode insert(BSTNode rt, int key) {
if (rt == null)
return new BSTNode(key);//找到插入位置,生成并返回一个结点的二叉搜索树,作为上一层的子结点。
//否则继续找要插入元素的位置
if (key < rt.key)
rt.left = insert(rt.left, key);
else if (key > rt.key)
rt.right = insert(rt.right, key);
return rt;
}
private boolean judge(BSTNode rt, int key) {
if (rt.flag) {//遍历过当前结点,故值为key应该继续往下插入
if (key == rt.key) return false; //K型二叉检索树中不可能出现重复的结点,当前序列出错
else { //判断值为key的结点的插入方向
if (key < rt.key) return judge(rt.left, key);
else return judge(rt.right, key);
}
} else {//当前结点没遍历过:要么是当前结点的插入位置,要么是序列不同
if (rt.key == key) {
rt.flag = true;
return true;
} else
return false;
}
}
private void resetTree(BSTNode rt) {
if (rt.left != null) resetTree(rt.left);
if (rt.right != null) resetTree(rt.right);
rt.flag = false;
}
}





















 276
276











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








