HDU 3377 Plan 解题报告（插头DP）

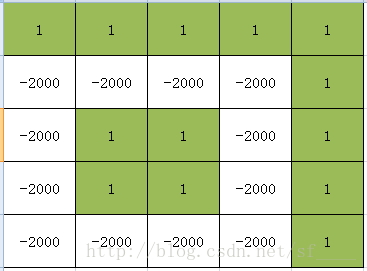
    解题报告：刚开始时卡了一下，以为用0，1表示插头即可，终点处判断有一个1插头就更新答案。后来想了一下，非起点到终点的部分可能成环，而结果也会被加进去。

    如下图：

    所以还是用以前Ural1519 的方法，使用括号序列。如果发现左插头为1，上插头为2，则放弃该状态。右下角如果有左插头亦或上插头，更新答案。

    如果不会插头DP，可以看我的上一篇博客：插头DP入门。

    代码如下：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int maxn = 100013;
int now,pre;
struct Node
{
	int H[maxn];
	int S[maxn];
	int N[maxn];
	int size;
	void init()
	{
		size=0;
		memset(H,-1,sizeof(H));
	}
	void push(int SS,int num)
	{
		int s=SS%maxn;
		while( ~H[s] && S[H[s]]!=SS )
			s=(s+1)%maxn;
		if( ~H[s] )
		{
			N[H[s]]=max(N[H[s]],num);
			return ;
		}

		S[size]=SS;
		N[size]=num;
		H[s]=size++;
	}
} dp[2];

int maze[10][10];

int get(int S,int p,int l=2)
{
	return (S>>(p*l))&((1<<l)-1);
}

void set(int &S,int p,int v,int l=2)
{
	S^=get(S,p,l)<<(p*l);
	S^=(v&((1<<l)-1))<<(p*l);
}

int main()
{
	int m,n;
	int cas=1;
	while(~scanf("%d%d",&n,&m))
	{
		for(int i=0;i<n;i++) for(int j=0;j<m;j++)
			scanf("%d",&maze[i][j]);

		now=1;
		pre=0;
		dp[now].init();
		dp[now].push(1,0);

		int ans=(1<<31);
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<m;j++)
			{
				swap(now,pre);
				dp[now].init();

				for(int s=0;s<dp[pre].size;s++)
				{
					int S=dp[pre].S[s];
					int num=dp[pre].N[s];
					int p=get(S,j);
					int q=get(S,j+1);

					if(p==0 && q==0)
					{
						dp[now].push(S,num);
						set(S,j,1);
						set(S,j+1,2);
						if(i<n-1 && j<m-1)
							dp[now].push(S,num+maze[i][j]);
					}
					else if((p>0) ^ (q>0))
					{
						if(i==n-1 && j==m-1)
						{
							set(S,j,0);
							set(S,j+1,0);
							if(S==0)
								ans=max(ans,num+maze[i][j]);
							continue;
						}
						if(i+(p>0)<n && j+(q>0)<m)
							dp[now].push(S,num+maze[i][j]);
						set(S,j,q);
						set(S,j+1,p);
						if(i+(q>0)<n && j+(p>0)<m)
							dp[now].push(S,num+maze[i][j]);
					}
					else if(p==2 && q==1)
					{
						set(S,j,0);
						set(S,j+1,0);
						dp[now].push(S,num+maze[i][j]);
					}
					else if(p==1 && q==2)
					{
					}
					else if(p==1 && q==1)
					{
						int find=1;
						for(int k=j+2;k<=m;k++)
						{
							int v=get(S,k);
							if(v==1)
								find++;
							else if(v==2)
								find--;
							if(find==0)
							{
								set(S,j,0);
								set(S,j+1,0);
								set(S,k,1);
								dp[now].push(S,num+maze[i][j]);
								break;
							}
						}
					}
					else if(p==2 && q==2)
					{
						int find=1;
						for(int k=j-1;k>=0;k--)
						{
							int v=get(S,k);
							if(v==2)
								find++;
							else if(v==1)
								find--;
							if(find==0)
							{
								set(S,j,0);
								set(S,j+1,0);
								set(S,k,2);
								dp[now].push(S,num+maze[i][j]);
								break;
							}
						}
					}
				}
			}

			for(int s=0;s<dp[now].size;s++)
				dp[now].S[s]<<=2;
		}

		printf("Case %d: %d\n",cas++,ans);
	}
}

     最小表示法：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;

const int maxn=59999;
const int L=3;
int now,pre;
int n,m;
int ans;
int endx,endy;
int maze[15][15];
int code[15],ch[15];
struct Node
{
	int h[maxn];
	int n[maxn];
	LL s[maxn];
	int size;
	void init()
	{
		memset(h,-1,sizeof(h));
		size=0;
	}

	void push(LL ss,int num)
	{
		int i=ss%maxn;
		while( ~h[i] && s[h[i]]!=ss )
			i=(i+1)%maxn;
		if( ~h[i] )
		{
			n[h[i]]=max(n[h[i]],num);
		}
		else
		{
			s[size]=ss;
			n[size]=num;
			h[i]=size++;
		}
	}
} dp[2];

void decode(LL s)
{
	for(int i=0;i<=m;i++)
		code[i]=s&((1<<L)-1),s>>=L;
}

LL encode()
{
	memset(ch,-1,sizeof(ch));
	ch[0]=0;
	LL s=0;
	int cnt=1;

	for(int i=m;i>=0;i--)
	{
		if( ch[code[i]]==-1 ) ch[code[i]]=cnt++;
		s<<=L;
		s|=ch[code[i]];
	}
	return s;
}

void shift()
{
	for(int s=0;s<dp[now].size;s++)
		dp[now].s[s]<<=L;
}

void merge(int a,int b)
{
	for(int i=0;i<=m;i++) if(code[i]==a)
		code[i]=b;
}

void doGrid(int i,int j)
{
	for(int s=0;s<dp[pre].size;s++)
	{
		decode(dp[pre].s[s]);
		int num=dp[pre].n[s];
		int left=code[j];
		int up=code[j+1];
		int ma=max(left,up);
		int mi=min(left,up);
		int val=maze[i][j];

		if(ma==0)
		{
			dp[now].push(encode(),num);
			if(i<n-1 && j<m-1)
			{
				code[j]=code[j+1]=13;
				dp[now].push(encode(),num+val);
			}
		}
		else if(mi==0)
		{
			if(i<n-1)
			{
				code[j]=ma;
				code[j+1]=0;
				dp[now].push(encode(),num+val);
			}
			if(j<m-1)
			{
				code[j]=0;
				code[j+1]=ma;
				dp[now].push(encode(),num+val);
			}
			if(i==n-1 && j==m-1)
			{
				code[j]=0;
				code[j+1]=0;
				if(encode()==0) ans=max(ans,num+val);
			}
		}
		else if(left==up)
		{
		}
		else
		{
			code[j]=code[j+1]=0;
			merge(left,up);
			dp[now].push(encode(),num+val);
		}
	}
}

void solve()
{
	now=1,pre=0;
	ans=(1<<31);
	dp[now].init();
	dp[now].push(1,0);

	for(int i=0;i<n;i++)
	{
		for(int j=0;j<m;j++)
		{
			swap(now,pre);
			dp[now].init();
			doGrid(i,j);
		}
		shift();
	}
}

void init()
{
	memset(maze,0,sizeof(maze));
	for(int i=0;i<n;i++)
		for(int j=0;j<m;j++)
			scanf("%d",&maze[i][j]);
}

int main()
{
	int cas=1;
	while(~scanf("%d%d",&n,&m))
	{
		init();
		solve();
		printf("Case %d: %d\n",cas++,ans);
	}
}