注:本文分析的C4.5代码是网上很流行的那份代码,非原创,本文只做代码分析
C4.5训练样本和测试样本来自 Matlab实现决策树C4.5算法并执行 作者:William_Dong
最后分析了tree的结构,只是初步理解,之后会运用新的样本集。
(高亮!!!!啊啊啊啊,疯了,这个C4.5的程序是错误的,
具体是连续属性那里分裂阈值的找寻方法错误!
求增益率的公式错误!!!
留着这篇博客是为了和正确的对比,时时提醒自己!!!
跑新的样本发现分裂的不对,找了5个小时bug,终于解决了,正确的程序及新的样本例子见下一篇博客~~~~~)
C4.5的程序如下: (错误的,再次提醒)
function test_targets = Use_C4_5(train_patterns, train_targets, test_patterns, inc_node, Nu)
% Classify using Quinlan's C4.5 algorithm
% Inputs:
% training_patterns - Train patterns 训练样本 每一列代表一个样本 每一行代表一个特征
% training_targets - Train targets 1×训练样本个数 每个训练样本对应的判别值
% test_patterns - Test patterns 测试样本,每一列代表一个样本
% inc_node - Percentage of incorrectly assigned samples at a node 一个节点上未正确分配的样本的百分比
% inc_node为防止过拟合,表示样本数小于一定阈值结束递归,可设置为5-10
% 注意inc_node设置太大的话会导致分类准确率下降,太小的话可能会导致过拟合
% Nu is to determine whether the variable is discrete or continuous (the value is always set to 10)
% Nu用于确定变量是离散还是连续(该值始终设置为10)
% 这里用10作为一个阈值,如果某个特征的无重复的特征值的数目比这个阈值还小,就认为这个特征是离散的
% Outputs
% test_targets - Predicted targets 1×测试样本个数 得到每个测试样本对应的判别值
% 也就是输出所有测试样本最终的判别情况
%NOTE: In this implementation it is assumed that a pattern vector with fewer than 10 unique values (the parameter Nu)
%is discrete, and will be treated as such. Other vectors will be treated as continuous
% 在该实现中,假设具有少于10个无重复值的特征向量(参数Nu)是离散的。 其他向量将被视为连续的
[Ni, M] = size(train_patterns); %M是训练样本数,Ni是训练样本维数,即是特征数目
inc_node = inc_node*M/100; % 5*训练样本数目/100
%Find which of the input patterns are discrete, and discretisize the corresponding dimension on the test patterns
%查找哪些输入模式(特征)是离散的,并离散测试模式上的相应维
discrete_dim = zeros(1,Ni); %用于记录每一个特征是否是离散特征,初始化都记为0,代表都是连续特征,
%如果后面更改,则意味着是离散特征,这个值会更改为这个离散特征的无重复特征值的数目
for i = 1:Ni %遍历每个特征
Ub = unique(train_patterns(i,:)); %取每个特征的不重复的特征值构成的向量
Nb = length(Ub); %得到无重复的特征值的数目
if (Nb <= Nu) %如果这个特征的无重复的特征值的数目比这个阈值还小,就认为这个特征是离散的
%This is a discrete pattern
discrete_dim(i) = Nb; %得到训练样本中,这个特征的无重复的特征值的数目 存放在discrete_dim(i)中,i表示第i个特征
dist = abs(ones(Nb ,1)*test_patterns(i,:) - Ub'*ones(1, size(test_patterns,2)));
%前面是把测试样本中,这个特征的那一行复制成Nb行,Nb是训练样本的这个特征中,无重复的特征值的数目
%后面是把这几个无重复的特征值构成的向量复制成测试样本个数列
%求这两个矩阵相应位置差的绝对值
[m, in] = min(dist); %找到每一列绝对差的最小值,构成m(1×样本数目) 并找到每一列绝对差最小值所在行的位置,构成in(1×样本数目)
%其实,这个in的中每个值就是代表了每个测试样本的特征值等于无重复的特征值中的哪一个或者更接近于哪一个
%如=3,就是指这个特征值等于无重复的特征值向量中的第3个或者更接近于无重复的特征值向量中的第3个
test_patterns(i,:) = Ub(in); %得到这个离散特征
end
end
%Build the tree recursively 递归地构造树
disp('Building tree')
tree = make_tree(train_patterns, train_targets, inc_node, discrete_dim, max(discrete_dim), 0);
%Classify test samples
disp('Classify test samples using the tree')
test_targets = use_tree(test_patterns, 1:size(test_patterns,2), tree, discrete_dim, unique(train_targets));
%1:size(test_patterns,2)其实是索引
%END Use_C4_5
function targets = use_tree(patterns, indices, tree, discrete_dim, Uc)
%Classify recursively using a tree
targets = zeros(1, size(patterns,2)); %设置每个样本的初始预测标签都是0
if (tree.dim == 0) %这说明达到了树的叶子节点
%Reached the end of the tree
targets(indices) = tree.child; %得到样本对应的标签是tree.child
return
end
%This is not the last level of the tree, so:
%First, find the dimension we are to work on
dim = tree.dim; %得到分裂特征
dims= 1:size(patterns,1); %得到特征索引
%And classify according to it 根据得到的决策树对测试样本进行分类
if (discrete_dim(dim) == 0) %如果当前分裂特征是个连续特征
%Continuous pattern
in = indices(find(patterns(dim, indices) <= tree.split_loc)); %找到当前测试样本中这个特征的特征值<=分裂值的样本索引
targets = targets + use_tree(patterns(dims, :), in, tree.child(1), discrete_dim(dims), Uc); %对这部分样本再分叉
in = indices(find(patterns(dim, indices) > tree.split_loc)); %找到当前测试样本中这个特征的特征值>分裂值的样本索引
targets = targets + use_tree(patterns(dims, :), in, tree.child(2), discrete_dim(dims), Uc); %对这部分样本再分叉
else %如果当前分裂特征是个离散特征
%Discrete pattern
Uf = unique(patterns(dim,:)); %得到这个样本集中这个特征的无重复特征值
for i = 1:length(Uf) %遍历每个特征值
if any(Uf(i) == tree.Nf) %tree.Nf为树的分类特征向量 当前所有样本的这个特征的特征值
in = indices(find(patterns(dim, indices) == Uf(i))); %找到当前测试样本中这个特征的特征值==分裂值的样本索引
targets = targets + use_tree(patterns(dims, :), in, tree.child(find(Uf(i)==tree.Nf)), discrete_dim(dims), Uc);%对这部分样本再分叉
end
end
end
%END use_tree
function tree = make_tree(patterns, targets, inc_node, discrete_dim, maxNbin, base)
% make_tree(train_patterns, train_targets, inc_node, discrete_dim, max(discrete_dim), 0);
%Build a tree recursively 递归地构造树
[Ni, L] = size(patterns); %%L为当前的样本总数,Ni为特征数目
Uc = unique(targets); %训练样本对应的判别标签 无重复的取得这些标签 也就是得到判别标签的个数
tree.dim = 0; %初始化树的分裂特征为第0个
%tree.child(1:maxNbin) = zeros(1,maxNbin);
tree.split_loc = inf; %初始化分裂位置是inf
if isempty(patterns)
return
end
%When to stop: If the dimension is one or the number of examples is small
% inc_node为防止过拟合,表示样本数小于一定阈值结束递归,可设置为5-10
if ((inc_node > L) | (L == 1) | (length(Uc) == 1)) %如果剩余训练样本太小(小于inc_node),或只剩一个,或只剩一类标签,退出
H = hist(targets, length(Uc)); %统计样本的标签,分别属于每个标签的数目 H(1×标签数目)
[m, largest] = max(H); %得到包含样本数最多的那个标签的索引,记为largest 包含多少个样本,记为m
tree.Nf = [];
tree.split_loc = [];
tree.child = Uc(largest);%姑且直接返回其中包含样本数最多一类作为其标签
return
end
%Compute the node's I
for i = 1:length(Uc) %遍历判别标签的数目
Pnode(i) = length(find(targets == Uc(i))) / L; %得到当前所有样本中 标签=第i个标签 的样本的数目 占样本总数的比例 存放在Pnode(i)中
end
% 计算当前的信息熵(分类期望信息)
% 例如,数据集D包含14个训练样本,9个属于类别“Yes”,5个属于类别“No”,Inode = -9/14 * log2(9/14) - 5/14 * log2(5/14) = 0.940
Inode = -sum(Pnode.*log(Pnode)/log(2));
%For each dimension, compute the gain ratio impurity %对于每维,计算杂质的增益比 对特征集中每个特征分别计算信息熵
%This is done separately for discrete and continuous patterns %对于离散和连续特征,分开计算
delta_Ib = zeros(1, Ni); %Ni是特征维数 用于记录每个特征的信息增益率
split_loc = ones(1, Ni)*inf; %初始化每个特征的分裂值是inf
for i = 1:Ni %遍历每个特征
data = patterns(i,:); %得到当前所有样本的这个特征的特征值
Ud = unique(data); %得到无重复的特征值构成向量Ud
Nbins = length(Ud); %得到无重复的特征值的数目
if (discrete_dim(i)) %如果这个特征是离散特征
%This is a discrete pattern
P = zeros(length(Uc), Nbins); %Uc是判别标签的个数 判别标签个数×无重复的特征值的数目
for j = 1:length(Uc) %遍历每个标签
for k = 1:Nbins %遍历每个特征值
indices = find((targets == Uc(j)) & (patterns(i,:) == Ud(k)));
% &适用于矩阵间的逻辑运算 &&不适用,只能用于单个元素 &的意思也是与
%找到 (样本标签==第j个标签 并且 当前所有样本的这个特征==第k个特征值) 的样本个数
P(j,k) = length(indices); %记为P(j,k)
end
end
Pk = sum(P); %取P的每一列的和,也就是得到当前所有样本中,这个特征的特征值==这个特征值的样本数目 Pk(1×特征值数目)表示这个特征的特征值等于每个特征值的样本数目
P = P/L; %得到当前所有样本中,这个特征的值等于每个特征值且标签等于每个标签的样本,占当前样本总数的比例
Pk = Pk/sum(Pk); %得到当前所有样本中,这个特征的值等于每个特征值的样本,占当前样本总数的比例
info = sum(-P.*log(eps+P)/log(2)); %对特征集中每个特征分别计算信息熵 info(1×特征值数目)
delta_Ib(i) = (Inode-sum(Pk.*info))/-sum(Pk.*log(eps+Pk)/log(2)); %计算得到当前特征的信息增益率
%计算信息增益率(GainRatio),公式为Gain(A)/I(A),
%其中Gain(A)=Inode-sum(Pk.*info)就是属性A的信息增益
%其中I(A)=-sum(Pk.*log(eps+Pk)/log(2))为属性A的所包含的信息
else %对于连续特征(主要要找到合适的分裂值,使数据离散化)
%This is a continuous pattern
P = zeros(length(Uc), 2); % P(判别标签数目×2) 列1代表前..个样本中的标签分布情况 列2代表除前..个样本之外的标签分布情况 这个..就是各个分裂位置
%Sort the patterns
[sorted_data, indices] = sort(data); %data里存放的是当前所有训练样本的这个特征的特征值 从小到大排序 sorted_data是排序好的数据 indices是索引
sorted_targets = targets(indices); %当然,判别标签也要随着样本顺序调整而调整
%Calculate the information for each possible split 计算分裂信息度量
I = zeros(1, L-1); %L-1=样本数-1
for j = 1:L-1
%for k =1:length(Uc) 遍历每个判别标签
% P(k,1) = sum(sorted_targets(1:j) == Uc(k)); %记录前j个样本的标签==第k个判别标签的数目
% P(k,2) = sum(sorted_targets(j+1:end) == Uc(k)); %记录除前j个样本外的样本标签==第k个判别标签的数目
%end
%%hist(y,x),表示以向量x的各个元素为统计范围,绘制y的分布情况。和上面注释掉的部分实现目的一样,但快速
P(:, 1) = hist(sorted_targets(1:j) , Uc); %记录前j个样本的标签的分布情况
P(:, 2) = hist(sorted_targets(j+1:end) , Uc); %记录除前j个样本外的样本标签的分布情况
Ps = sum(P)/L; %sum(P)是得到分裂位置前面和后面各有样本数占当前样本总数的比例
P = P/L; %占样本总数的比例
Pk = sum(P); %%sum(P)是得到分裂位置前面和后面各有多少个样本
P1 = repmat(Pk, length(Uc), 1); %把Pk复制成 判别标签个数 行
P1 = P1 + eps*(P1==0);
%若P1中所有数都不为0,P1 = P1 + eps*0,P1就等于之前的P1
%而若P1中有的数==0,P1 = P1 + eps*1 P1就不再等于之前的P1
info = sum(-P.*log(eps+P./P1)/log(2)); %计算信息熵(分类期望信息)
I(j) = Inode - sum(info.*Ps); %Inode-sum(info.*Ps)就是以第j个样本分裂的的信息增益
end
[delta_Ib(i), s] = max(I); %找到信息增益最大的划分方法 delta_Ib(i)中存放的是对于当前第i个特征而言,最大的信息增益作为这个特征的信息增益 s存放这个划分方法
split_loc(i) = sorted_data(s); %对应特征i的划分位置就是能使信息增益最大的划分值
end
end
%Find the dimension minimizing delta_Ib %找到当前要作为分裂特征的特征
[m, dim] = max(delta_Ib); %找到所有特征中最大的信息增益对应的特征,记为dim
dims = 1:Ni; %Ni特征数目
tree.dim = dim; %记为树的分裂特征
%Split along the 'dim' dimension
Nf = unique(patterns(dim,:)); %得到选择的这个作为分裂特征的特征的那一行 也就是得到当前所有样本的这个特征的特征值
Nbins = length(Nf); %得到这个特征的无重复的特征值的数目
tree.Nf = Nf; %记为树的分类特征向量 当前所有样本的这个特征的特征值
tree.split_loc = split_loc(dim); %把这个特征的划分位置记为树的分裂位置 可是如果选择的是一个离散特征,split_loc(dim)是初始值inf啊???
%If only one value remains for this pattern, one cannot split it.
if (Nbins == 1) %无重复的特征值的数目==1,即这个特征只有这一个特征值,就不能进行分裂
H = hist(targets, length(Uc)); %统计当前所有样本的标签,分别属于每个标签的数目 H(1×标签数目)
[m, largest] = max(H); %得到包含样本数最多的那个标签的索引,记为largest 包含多少个样本,记为m
tree.Nf = []; %因为不以这个特征进行分裂,所以Nf和split_loc都为空
tree.split_loc = [];
tree.child = Uc(largest); %姑且将这个特征的标签就记为包含样本数最多的那个标签
return
end
if (discrete_dim(dim)) %如果当前选择的这个作为分裂特征的特征是个离散特征
%Discrete pattern
for i = 1:Nbins %遍历这个特征下无重复的特征值的数目
indices = find(patterns(dim, :) == Nf(i)); %找到当前所有样本的这个特征的特征值为Nf(i)的索引们
tree.child(i) = make_tree(patterns(dims, indices), targets(indices), inc_node, discrete_dim(dims), maxNbin, base);%递归
%因为这是个离散特征,所以分叉成Nbins个,分别针对每个特征值里的样本,进行再分叉
end
else
%Continuous pattern %如果当前选择的这个作为分裂特征的特征是个连续特征
indices1 = find(patterns(dim,:) <= split_loc(dim)); %找到特征值<=分裂值的样本的索引们
indices2 = find(patterns(dim,:) > split_loc(dim)); %找到特征值>分裂值的样本的索引们
if ~(isempty(indices1) | isempty(indices2)) %如果<=分裂值 >分裂值的样本数目都不等于0
tree.child(1) = make_tree(patterns(dims, indices1), targets(indices1), inc_node, discrete_dim(dims), maxNbin, base+1);%递归
%对<=分裂值的样本进行再分叉
tree.child(2) = make_tree(patterns(dims, indices2), targets(indices2), inc_node, discrete_dim(dims), maxNbin, base+1);%递归
%对>分裂值的样本进行再分叉
else
H = hist(targets, length(Uc)); %统计当前所有样本的标签,分别属于每个标签的数目 H(1×标签数目)
[m, largest] = max(H); %得到包含样本数最多的那个标签的索引,记为largest 包含多少个样本,记为m
tree.child = Uc(largest); %姑且将这个特征的标签就记为包含样本数最多的那个标签
tree.dim = 0; %树的分裂特征记为0
end
end
C4.5 的调用程序如下: train_and_test_with_C4_5.m
%用75个样本,每个样本有4个特征,来训练
traindata=[
5 3 1.6 0.2 1
5 3.4 1.6 0.4 1
5.2 3.5 1.5 0.2 1
5.2 3.4 1.4 0.2 1
4.7 3.2 1.6 0.2 1
4.8 3.1 1.6 0.2 1
5.4 3.4 1.5 0.4 1
5.2 4.1 1.5 0.1 1
5.5 4.2 1.4 0.2 1
4.9 3.1 1.5 0.2 1
5 3.2 1.2 0.2 1
5.5 3.5 1.3 0.2 1
4.9 3.6 1.4 0.1 1
4.4 3 1.3 0.2 1
5.1 3.4 1.5 0.2 1
5 3.5 1.3 0.3 1
4.5 2.3 1.3 0.3 1
4.4 3.2 1.3 0.2 1
5 3.5 1.6 0.6 1
5.1 3.8 1.9 0.4 1
4.8 3 1.4 0.3 1
5.1 3.8 1.6 0.2 1
4.6 3.2 1.4 0.2 1
5.3 3.7 1.5 0.2 1
5 3.3 1.4 0.2 1
6.6 3 4.4 1.4 2
6.8 2.8 4.8 1.4 2
6.7 3 5 1.7 2
6 2.9 4.5 1.5 2
5.7 2.6 3.5 1 2
5.5 2.4 3.8 1.1 2
5.5 2.4 3.7 1 2
5.8 2.7 3.9 1.2 2
6 2.7 5.1 1.6 2
5.4 3 4.5 1.5 2
6 3.4 4.5 1.6 2
6.7 3.1 4.7 1.5 2
6.3 2.3 4.4 1.3 2
5.6 3 4.1 1.3 2
5.5 2.5 4 1.3 2
5.5 2.6 4.4 1.2 2
6.1 3 4.6 1.4 2
5.8 2.6 4 1.2 2
5 2.3 3.3 1 2
5.6 2.7 4.2 1.3 2
5.7 3 4.2 1.2 2
5.7 2.9 4.2 1.3 2
6.2 2.9 4.3 1.3 2
5.1 2.5 3 1.1 2
5.7 2.8 4.1 1.3 2
7.2 3.2 6 1.8 3
6.2 2.8 4.8 1.8 3
6.1 3 4.9 1.8 3
6.4 2.8 5.6 2.1 3
7.2 3 5.8 1.6 3
7.4 2.8 6.1 1.9 3
7.9 3.8 6.4 2 3
6.4 2.8 5.6 2.2 3
6.3 2.8 5.1 1.5 3
6.1 2.6 5.6 1.4 3
7.7 3 6.1 2.3 3
6.3 3.4 5.6 2.4 3
6.4 3.1 5.5 1.8 3
6 3 4.8 1.8 3
6.9 3.1 5.4 2.1 3
6.7 3.1 5.6 2.4 3
6.9 3.1 5.1 2.3 3
5.8 2.7 5.1 1.9 3
6.8 3.2 5.9 2.3 3
6.7 3.3 5.7 2.5 3
6.7 3 5.2 2.3 3
6.3 2.5 5 1.9 3
6.5 3 5.2 2 3
6.2 3.4 5.4 2.3 3
5.9 3 5.1 1.8 3
];
%用75个样本测试
testdata=[
5.1 3.5 1.4 0.2 1
4.9 3 1.4 0.2 1
4.7 3.2 1.3 0.2 1
4.6 3.1 1.5 0.2 1
5 3.6 1.4 0.2 1
5.4 3.9 1.7 0.4 1
4.6 3.4 1.4 0.3 1
5 3.4 1.5 0.2 1
4.4 2.9 1.4 0.2 1
4.9 3.1 1.5 0.1 1
5.4 3.7 1.5 0.2 1
4.8 3.4 1.6 0.2 1
4.8 3 1.4 0.1 1
4.3 3 1.1 0.1 1
5.8 4 1.2 0.2 1
5.7 4.4 1.5 0.4 1
5.4 3.9 1.3 0.4 1
5.1 3.5 1.4 0.3 1
5.7 3.8 1.7 0.3 1
5.1 3.8 1.5 0.3 1
5.4 3.4 1.7 0.2 1
5.1 3.7 1.5 0.4 1
4.6 3.6 1 0.2 1
5.1 3.3 1.7 0.5 1
4.8 3.4 1.9 0.2 1
7 3.2 4.7 1.4 2
6.4 3.2 4.5 1.5 2
6.9 3.1 4.9 1.5 2
5.5 2.3 4 1.3 2
6.5 2.8 4.6 1.5 2
5.7 2.8 4.5 1.3 2
6.3 3.3 4.7 1.6 2
4.9 2.4 3.3 1 2
6.6 2.9 4.6 1.3 2
5.2 2.7 3.9 1.4 2
5 2 3.5 1 2
5.9 3 4.2 1.5 2
6 2.2 4 1 2
6.1 2.9 4.7 1.4 2
5.6 2.9 3.6 1.3 2
6.7 3.1 4.4 1.4 2
5.6 3 4.5 1.5 2
5.8 2.7 4.1 1 2
6.2 2.2 4.5 1.5 2
5.6 2.5 3.9 1.1 2
5.9 3.2 4.8 1.8 2
6.1 2.8 4 1.3 2
6.3 2.5 4.9 1.5 2
6.1 2.8 4.7 1.2 2
6.4 2.9 4.3 1.3 2
6.3 3.3 6 2.5 3
5.8 2.7 5.1 1.9 3
7.1 3 5.9 2.1 3
6.3 2.9 5.6 1.8 3
6.5 3 5.8 2.2 3
7.6 3 6.6 2.1 3
4.9 2.5 4.5 1.7 3
7.3 2.9 6.3 1.8 3
6.7 2.5 5.8 1.8 3
7.2 3.6 6.1 2.5 3
6.5 3.2 5.1 2 3
6.4 2.7 5.3 1.9 3
6.8 3 5.5 2.1 3
5.7 2.5 5 2 3
5.8 2.8 5.1 2.4 3
6.4 3.2 5.3 2.3 3
6.5 3 5.5 1.8 3
7.7 3.8 6.7 2.2 3
7.7 2.6 6.9 2.3 3
6 2.2 5 1.5 3
6.9 3.2 5.7 2.3 3
5.6 2.8 4.9 2 3
7.7 2.8 6.7 2 3
6.3 2.7 4.9 1.8 3
6.7 3.3 5.7 2.1 3
];
train_patterns=traindata(:,1:(size(traindata,2)-1)); %得到训练样本
train_targets=traindata(:,size(traindata,2))'; %得到训练样本的标签 1×训练样本数目
test_patterns=testdata(:,1:(size(testdata,2)-1)); %得到测试样本
test_targets=testdata(:,size(testdata,2))'; %得到测试样本的真实标签,用于一会儿和预测标签对比
test_targets_predict = Use_C4_5(train_patterns', train_targets, test_patterns', 5, 10);
%train_patterns'行是feature,列是样本
c_count=sum(test_targets==test_targets_predict);%得到真实和预测相同的数目
accuracy=c_count/size(test_targets,2); %计算正确率
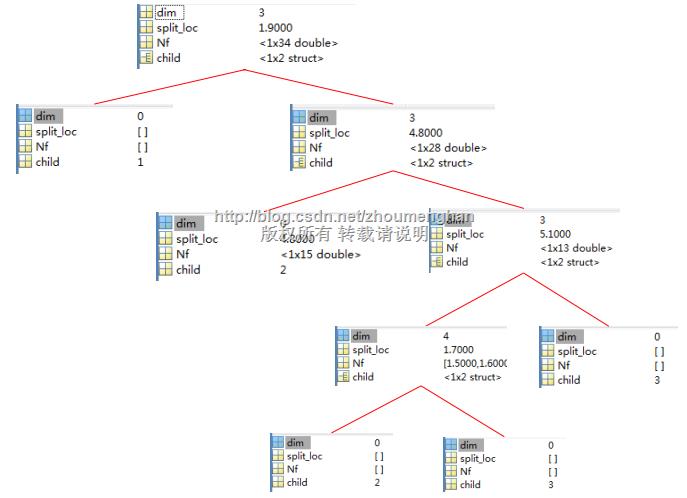
fprintf('针对此测试样本的标签预测正确率为%f',accuracy); 根据训练样本得到的决策树在matlab中存储结构:
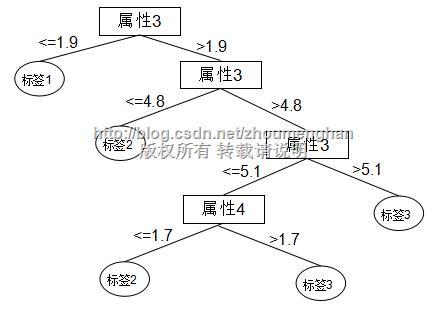
也就是说,这棵决策树是这样的:






















 2832
2832

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








