If A is an m × n matrix and B is a p × q matrix, then the Kronecker product A ⊗ B is the mp × nq block matrix:
more explicitly:
More compactly, we have 
If A and B represent linear transformations V1 → W1 and V2 → W2, respectively, then A ⊗ B represents the tensor product of the two maps, V1 ⊗ V2 → W1 ⊗ W2.









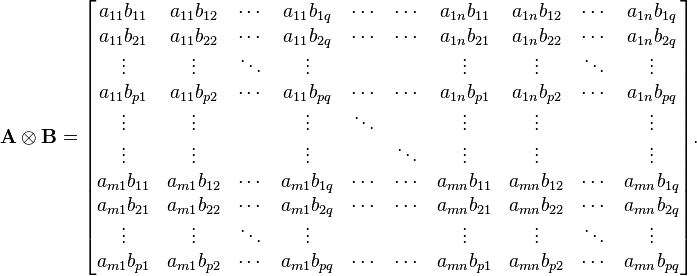
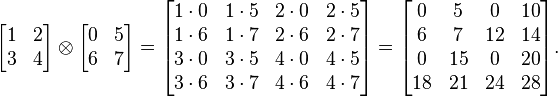
















 6729
6729

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








