在学习 matlab 的过程中遇到了一些困惑,记录一下。
一、cumsum函数
- 定义:求元素累积和向量。详解请见 link。
- 举例:
% 定义一个 3*3*3 矩阵
X = [1 -2 3; 4 5 -6; -7 8 9];
Y = [7 8 0; 4 -5 6; 1 2 -4];
Z = [-2 -4 6; 7 3 -1; 9 5 -3];
M(:, :, 1) = X;
M(:, :, 2) = Y;
M(:, :, 3) = Z;
结果如下:
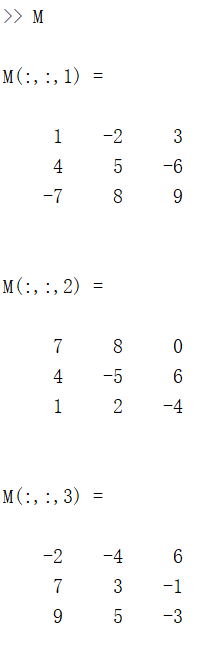
% 求元素累积和向量:
C1 = cumsum(M); % 沿矩阵M的第一个尺寸不为 1 的维度计算,C1 与 M 尺寸相等
C2 = cumsum(M, 1); % 沿第一维计算
C3 = cumsum(M, 2); % 沿第二维计算
C4 = cumsum(M, 3); % 沿第三维计算
C5 = cumsum(M, 'forward'); % 前向方向,从开始到结尾
C6 = cumsum(M, 'reverse'); % 反向方向。从结尾到开始
C7 = cumsum(X);
对于一个 3 * 3 * 3 的矩阵,第一个尺寸不为 1 的维就是列的方向,矩阵中第 m 行第 n 列元素是 M 中第 1 行到第 m 行的所有第 n 列元素的累加和。
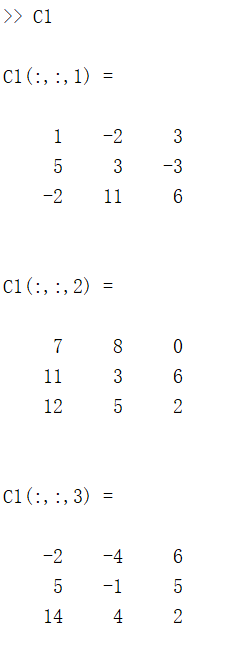

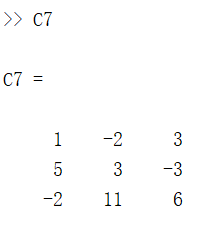
同理:
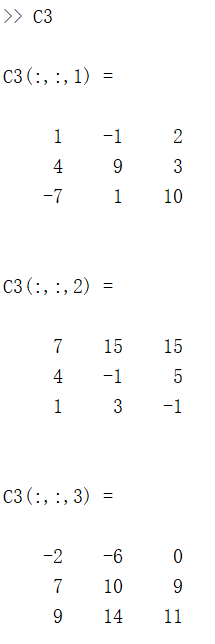
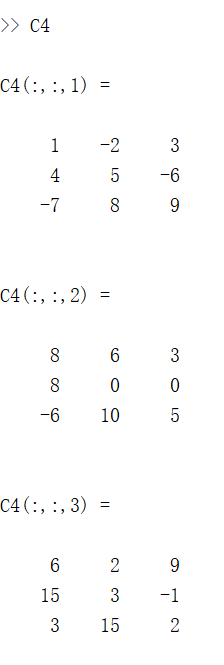
正向的计算就是从上往下计算(例如从第一行开始逐行往下加),反向计算就是从下往上计算(例如从最后一行开始逐行往上加):
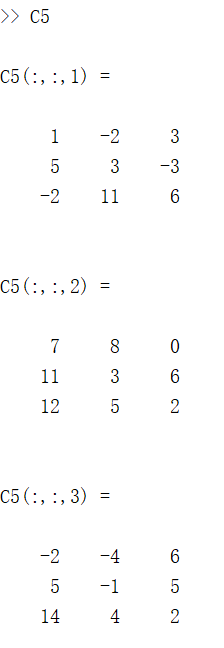
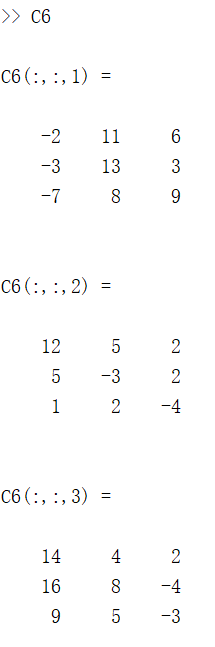
二、cumprod函数
- 定义:求元素累积向量。有了对 cumsum 函数的理解,理解这个函数就容易多了,用法也都是类似的。
- 直接上代码:
% 求元素累积向量:
P1 = cumprod(M);
P2 = cumprod(M, 1);
P3 = cumprod(M, 2);
P4 = cumprod(M, 3);
P5 = cumprod(M, 'forward');
P6 = cumprod(M, 'reverse');
P7 = cumprod(X);
结果如下:

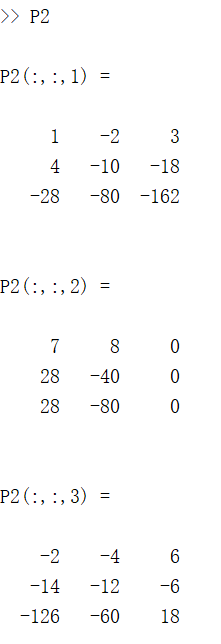
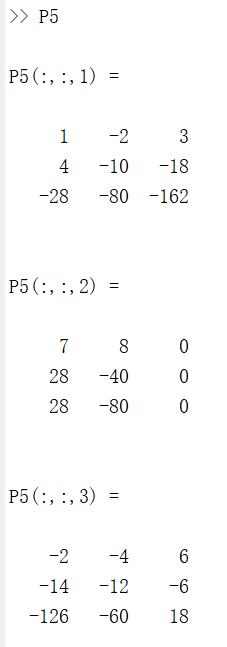
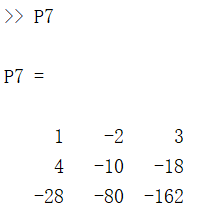
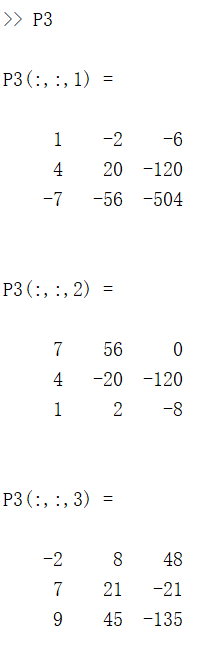
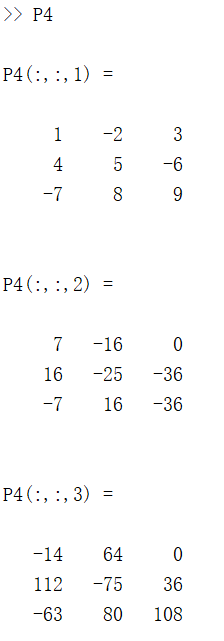
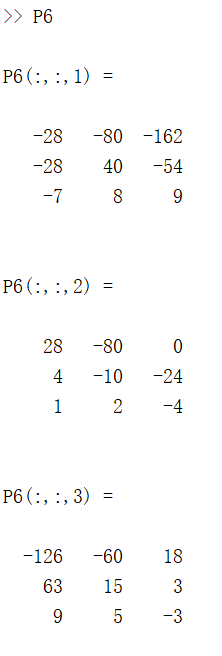
三、mean函数
在这里记录一个小插曲。我在计算 M 矩阵的均值的时候,写了如下一行代码:
% 求均值
mean = mean(M);
第一次运行时没有出现任何问题,均值也顺利计算出来,如下图所示:

但是后面运行时就出现了如下错误:

将变量名改为 mean1 或者 a 之类的也不行。重新打开之后也是一样的情况,第一次运行没有问题,后面运行就会报错。
查看了一下别人的解决方案,这位将这个错误解释的比较清楚,解决方案参考这位。
四、var函数
- 定义:求方差。
- 首先要搞懂什么是方差。
方差用于衡量随机变量或一组数据的离散程度,方差在在统计描述和概率分布中有不同的定义和计算公式。①概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度;②统计中的方差(样本方差)是每个样本值与全体样本均值之差的平方值的平均数,代表每个变量与总体均值间的离散程度。。
求求大家快去看这篇帖子,讲得真的很详细!!!(连样本方差分母为什么为 n-1 都有引用解释)
- 好了,上代码。
>> X-mean(:, :, 1)
ans =
1.6667 -5.6667 1.0000
4.6667 1.3333 -8.0000
-6.3333 4.3333 7.0000
>> [X-mean(:, :, 1)].^2
ans =
2.7778 32.1111 1.0000
21.7778 1.7778 64.0000
40.1111 18.7778 49.0000
>> sum([X-mean(:, :, 1)].^2)
ans =
64.6667 52.6667 114.0000
>> (sum([X-mean(:, :, 1)].^2))/2
ans =
32.3333 26.3333 57.0000
>>
这里先以二维矩阵为例进行分步计算。 mean 就是第三部分提到过的 M 矩阵的均值。计算 X 的方差流程如上图所示。下面验证下:
>> var(X)
ans =
32.3333 26.3333 57.0000
没毛病。可见在 matlab 中,不特殊强调的情况下都是按列进行计算的。
扩展至三维矩阵:
>> var(M)
ans(:,:,1) =
32.3333 26.3333 57.0000
ans(:,:,2) =
9.0000 42.3333 25.3333
ans(:,:,3) =
34.3333 22.3333 22.3333
一样的道理。
- (1)按第一维、第二维、第三维求方差:
>> var(M, [], 1) % 按第一维求方差,与 var(M) 结果一样
ans(:,:,1) =
32.3333 26.3333 57.0000
ans(:,:,2) =
9.0000 42.3333 25.3333
ans(:,:,3) =
34.3333 22.3333 22.3333
>> var(M, [], 2) % 按行求方差
ans(:,:,1) =
6.3333
37.0000
80.3333
ans(:,:,2) =
19.0000
34.3333
10.3333
ans(:,:,3) =
28.0000
16.0000
37.3333
>> var(M, [], 3) % 按第三维求方差
ans =
21.0000 41.3333 9.0000
3.0000 28.0000 36.3333
64.0000 9.0000 52.3333
(2)在一二维、二三维中求方差:
>> var(M, [], [1, 2]) % 在一二维中求方差
ans(:,:,1) =
32.5000
ans(:,:,2) =
21.3611
ans(:,:,3) =
23.1944
>> var(M, [], [2, 3])
ans =
18.8611
22.6111
35.6944
求一二维的方差时,可先将一二维看成一个整体,即求三个 3 * 3 矩阵的方差。求二三位相同的道理。
(3)需要注意的是, var 函数增加了一个权重 W 参数。
V = var(A,w) specifies a weighting scheme. When w = 0 (default), V is normalized by the number of observations-1. When w = 1, it is normalized by the number of observations. w can also be a weight vector containing nonnegative elements. In this case, the length of w must equal the length of the dimension over which var is operating.
V = var(A,w) :当 W=0 时,使用 N-1 归一化;当 W=1 时,使用 N 归一化;W是包含非负元素的权重向量时,长度必须等于 var 将作用于的维度的长度。
>> V9 = var(M, 0) % 用 N-1 归一化,结果与var(M)一样
V9(:,:,1) =
32.3333 26.3333 57.0000
V9(:,:,2) =
9.0000 42.3333 25.3333
V9(:,:,3) =
34.3333 22.3333 22.3333
>> var(M, 1) % 用 N 归一化
ans(:,:,1) =
21.5556 17.5556 38.0000
ans(:,:,2) =
6.0000 28.2222 16.8889
ans(:,:,3) =
22.8889 14.8889 14.8889
>> var(M, [2 3 4]) % 用[2 3 4]归一化
ans(:,:,1) =
24.9136 14.8395 42.8889
ans(:,:,2) =
5.5556 23.3333 19.0617
ans(:,:,3) =
18.5432 12.2222 12.2222
对于这个按权重求方差的过程,chatGPT给出的步骤如下:
1.计算加权平均值(weighted mean):
加权平均值的计算公式为:weighted_mean = (w1 * x1 + w2 * x2 + … + wn * xn) / (w1 + w2 + … + wn),其中 xi 表示第 i 个数据点,wi 表示第 i 个数据点的权重。
2.计算每个数据点与加权平均值的差值的平方,并乘以对应的权重:
对于每个数据点 xi,计算 (xi - weighted_mean)^2 * wi。
3.求和所有乘积结果:
将步骤 2 中得到的乘积结果求和:sum((xi - weighted_mean)^2 * wi)。
4.计算加权方差(weighted variance):
加权方差的计算公式为:weighted_variance = sum((xi - weighted_mean)^2 * wi) / (w1 + w2 + … + wn)。
为了搞懂这个过程,我们先举两个简单的例子:
① 假设 A1 为一个 1 * 3 的数组:
>> A1 = [1 2 3]
A1 =
1 2 3
>> w = [0.5 0.25 0.25]
w =
0.5000 0.2500 0.2500
>> A1.*w
ans =
0.5000 0.5000 0.7500
>> sum(A1.*w)
ans =
1.7500
>> sum(A1.*w)/sum(w)
ans =
1.7500
>> A1-sum(A1.*w)/sum(w)
ans =
-0.7500 0.2500 1.2500
>> (A1-sum(A1.*w)/sum(w)).^2
ans =
0.5625 0.0625 1.5625
>> ((A1-sum(A1.*w)/sum(w)).^2).*w
ans =
0.2812 0.0156 0.3906
>> sum(((A1-sum(A1.*w)/sum(w)).^2).*w)
ans =
0.6875
>> (sum(((A1-sum(A1.*w)/sum(w)).^2).*w))/(sum(w))
ans =
0.6875
>> var(A1, w)
ans =
0.6875
② 假设 A1 为一个 3 * 1 的矩阵:
>> A1 = [1; 2; 3]
A1 =
1
2
3
>> w = [0.5 0.25 0.25]
w =
0.5000 0.2500 0.2500
>> var(A1, w)
ans =
0.6875
计算过程同上。
③ 好了,来看我们的 3 * 3 * 3 M 矩阵:
>> w = [2 3 4]
w =
2 3 4
>> M.*w
ans(:,:,1) =
2 -6 12
8 15 -24
-14 24 36
ans(:,:,2) =
14 24 0
8 -15 24
2 6 -16
ans(:,:,3) =
-4 -12 24
14 9 -4
18 15 -12
>> (M.*w)/sum(w) % 求加权平均值
ans(:,:,1) =
0.2222 -0.6667 1.3333
0.8889 1.6667 -2.6667
-1.5556 2.6667 4.0000
ans(:,:,2) =
1.5556 2.6667 0
0.8889 -1.6667 2.6667
0.2222 0.6667 -1.7778
ans(:,:,3) =
-0.4444 -1.3333 2.6667
1.5556 1.0000 -0.4444
2.0000 1.6667 -1.3333
>> M-(M.*w)/sum(w)
ans(:,:,1) =
0.7778 -1.3333 1.6667
3.1111 3.3333 -3.3333
-5.4444 5.3333 5.0000
ans(:,:,2) =
5.4444 5.3333 0
3.1111 -3.3333 3.3333
0.7778 1.3333 -2.2222
ans(:,:,3) =
-1.5556 -2.6667 3.3333
5.4444 2.0000 -0.5556
7.0000 3.3333 -1.6667
>> (M-(M.*w)/sum(w)).^2
ans(:,:,1) =
0.6049 1.7778 2.7778
9.6790 11.1111 11.1111
29.6420 28.4444 25.0000
ans(:,:,2) =
29.6420 28.4444 0
9.6790 11.1111 11.1111
0.6049 1.7778 4.9383
ans(:,:,3) =
2.4198 7.1111 11.1111
29.6420 4.0000 0.3086
49.0000 11.1111 2.7778
>> ((M-(M.*w)/sum(w)).^2).*w
ans(:,:,1) =
1.2099 5.3333 11.1111
19.3580 33.3333 44.4444
59.2840 85.3333 100.0000
ans(:,:,2) =
59.2840 85.3333 0
19.3580 33.3333 44.4444
1.2099 5.3333 19.7531
ans(:,:,3) =
4.8395 21.3333 44.4444
59.2840 12.0000 1.2346
98.0000 33.3333 11.1111
>> sum(((M-(M.*w)/sum(w)).^2).*w)
ans(:,:,1) =
79.8519 124.0000 155.5556
ans(:,:,2) =
79.8519 124.0000 64.1975
ans(:,:,3) =
162.1235 66.6667 56.7901
>> sum(((M-(M.*w)/sum(w)).^2).*w)/sum(w) % 求加权方差
ans(:,:,1) =
8.8724 13.7778 17.2840
ans(:,:,2) =
8.8724 13.7778 7.1331
ans(:,:,3) =
18.0137 7.4074 6.3100
我们看到与直接调用 var 函数得到的结果是不同的:
>> var(M,w)
ans(:,:,1) =
24.9136 14.8395 42.8889
ans(:,:,2) =
5.5556 23.3333 19.0617
ans(:,:,3) =
18.5432 12.2222 12.2222
这是因为我们所给的权重矩阵对应的应该是我们所操作的维度,这里没有指定维度,就是默认的第一个长度非 1 的维度,也就是说我们实际上实在对列进行操作。而我们在第一步 M.*w 时是对行进行操作,所以结果不对。我们在进行运算时需要对权重矩阵进行一个转置。正确操作如下:
>> M.*w'
ans(:,:,1) =
2 -4 6
12 15 -18
-28 32 36
ans(:,:,2) =
14 16 0
12 -15 18
4 8 -16
ans(:,:,3) =
-4 -8 12
21 9 -3
36 20 -12
>> sum(M.*w')
ans(:,:,1) =
-14 43 24
ans(:,:,2) =
30 9 2
ans(:,:,3) =
53 21 -3
>> sum(M.*w')/sum(w) % 求加权平均值
ans(:,:,1) =
-1.5556 4.7778 2.6667
ans(:,:,2) =
3.3333 1.0000 0.2222
ans(:,:,3) =
5.8889 2.3333 -0.3333
>> M-sum(M.*w')/sum(w)
ans(:,:,1) =
2.5556 -6.7778 0.3333
5.5556 0.2222 -8.6667
-5.4444 3.2222 6.3333
ans(:,:,2) =
3.6667 7.0000 -0.2222
0.6667 -6.0000 5.7778
-2.3333 1.0000 -4.2222
ans(:,:,3) =
-7.8889 -6.3333 6.3333
1.1111 0.6667 -0.6667
3.1111 2.6667 -2.6667
>> (M-sum(M.*w')/sum(w)).^2
ans(:,:,1) =
6.5309 45.9383 0.1111
30.8642 0.0494 75.1111
29.6420 10.3827 40.1111
ans(:,:,2) =
13.4444 49.0000 0.0494
0.4444 36.0000 33.3827
5.4444 1.0000 17.8272
ans(:,:,3) =
62.2346 40.1111 40.1111
1.2346 0.4444 0.4444
9.6790 7.1111 7.1111
>> ((M-sum(M.*w')/sum(w)).^2).*w'
ans(:,:,1) =
13.0617 91.8765 0.2222
92.5926 0.1481 225.3333
118.5679 41.5309 160.4444
ans(:,:,2) =
26.8889 98.0000 0.0988
1.3333 108.0000 100.1481
21.7778 4.0000 71.3086
ans(:,:,3) =
124.4691 80.2222 80.2222
3.7037 1.3333 1.3333
38.7160 28.4444 28.4444
>> sum(((M-sum(M.*w')/sum(w)).^2).*w') % 求加权方差
ans(:,:,1) =
224.2222 133.5556 386.0000
ans(:,:,2) =
50.0000 210.0000 171.5556
ans(:,:,3) =
166.8889 110.0000 110.0000
>> sum(((M-sum(M.*w')/sum(w)).^2).*w')/sum(w)
ans(:,:,1) =
24.9136 14.8395 42.8889
ans(:,:,2) =
5.5556 23.3333 19.0617
ans(:,:,3) =
18.5432 12.2222 12.2222
(4)同样的,对于加权的方差,我们也可以指定维度和向量:
V = var(A,w,dim)
V = var(A,w,vecdim)
具体的与前面一样,不再赘述。
五、std函数
- 定义:求标准差
- link
- 求标准差的格式、参数及含义同 var 函数一致。
六、cov函数
- 定义:求协方差
- 什么是协方差?link、link
- (1)cov(X):求向量 X 的方差或矩阵 X 的协方差矩阵。矩阵 X 每行是一个观察值,每列是一个变量;当 N > 1 时,采用 N-1 归一化;当 N=1 时,采用 N 归一化。
>> A1 = [1 2 3]
A1 =
1 2 3
>> cov(A1)
ans =
1
>> var(A1)
ans =
1
对于如何求矩阵的协方差矩阵,chatGPT 给出的步骤如下:
要计算矩阵的协方差矩阵,首先需要有一个包含多个样本的矩阵,每行表示一个样本,每列表示一个特征。假设有一个n 行 m 列的矩阵 X,其中 m 是样本数,n 是特征数。协方差矩阵的计算步骤如下:
1.对每个特征的样本进行去均值处理:
对矩阵每列进行去均值操作,即将每个元素减去该列的均值。
2.计算去均值后的矩阵的转置矩阵:
将步骤 1 得到的矩阵进行转置,得到一个 m 行 n 列的矩阵 Xt。
3.计算协方差矩阵:
将去均值后的矩阵 X 乘以转置矩阵 Xt,并除以样本数 m-1,得到一个 n 行 n 列的协方差矩阵 Cov。
Cov = (X * Xt) / (m-1)
注意:协方差矩阵是一个对称矩阵,对角线上的元素表示各个特征的方差,非对角线上的元素表示不同特征之间的协方差。
当我对 3 * 3 * 3 的矩阵 M 求协方差矩阵时,matlab 显示输入必须为二维。
(2)diag(cov(X)) 是每一列的方差向量;sqrt(diag(cov(X))) 是标准差向量。
实际就是取了协方差矩阵的对角线(每个向量的方差),又开了平方。
(3)cov(X, Y):求矩阵 X 和 Y 的协方差矩阵,X 和 Y 维数相等。
根据我个人的理解,因为这个地方是 X 和 Y 两个变量,所以最终求出来的协方差矩阵就是 2*2 矩阵。
>> cov(X, Y)
ans =
32.5000 -14.0833
-14.0833 21.3611
按照从左往右,从上往下的顺序,这四个值分别为 cov(X, X), cov(X, Y), cov(Y, X), cov(Y, Y)。验证一下:
>> cov(X, X)
ans =
32.5000 32.5000
32.5000 32.5000
>> cov(Y, Y)
ans =
21.3611 21.3611
21.3611 21.3611
没毛病。那么这几个数怎么来的呢?按照定义,cov(X, X) 显然就是 var(X)。计算过程如下:
>> mean(X, 'all')
ans =
1.6667
>> X-mean(X, 'all')
ans =
-0.6667 -3.6667 1.3333
2.3333 3.3333 -7.6667
-8.6667 6.3333 7.3333
>> (X-mean(X, 'all')).^2
ans =
0.4444 13.4444 1.7778
5.4444 11.1111 58.7778
75.1111 40.1111 53.7778
>> sum((X-mean(X, 'all')).^2, 'all')
ans =
260
>> sum((X-mean(X, 'all')).^2, 'all')/8 % 注意这个地方分子为8,也就是(m-1)
ans =
32.5000
cov(Y, Y) 计算过程类似。
对于 cov(X, Y),也是一样的道理,计算过程如下:
>> mean(X, 'all')
ans =
1.6667
>> X-mean(X, 'all')
ans =
-0.6667 -3.6667 1.3333
2.3333 3.3333 -7.6667
-8.6667 6.3333 7.3333
>> mean(Y, 'all')
ans =
2.1111
>> Y-mean(Y, 'all')
ans =
4.8889 5.8889 -2.1111
1.8889 -7.1111 3.8889
-1.1111 -0.1111 -6.1111
>> (X-mean(X, 'all')).*(Y-mean(Y, 'all'))
ans =
-3.2593 -21.5926 -2.8148
4.4074 -23.7037 -29.8148
9.6296 -0.7037 -44.8148
>> sum((X-mean(X, 'all')).*(Y-mean(Y, 'all')), 'all')
ans =
-112.6667
>> sum((X-mean(X, 'all')).*(Y-mean(Y, 'all')), 'all')/8
ans =
-14.0833





















 1475
1475











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








