1️⃣1️⃣three.js_物体的平移、缩放、旋转

11、物体的平移、缩放、旋转

• 3D虚拟工厂在线体验

• 在父级坐标系中，物体的缩放和旋转看似简单——无非是改变大小或调整角度，实则暗藏玄机，变得复杂难懂。

   //先定位办公楼
    const tempScene = scene.children.find(t => t.name == 'Scene')
    const tempOffice= tempScene.children.find(t => t.name == '办公楼');   
  
    const worldPosition = new THREE.Vector3();
    let newOffice1 = tempOffice.clone();     
    console.log('局部坐标(移动前):', newOffice1.position);
    newOffice1.position.set(150,0,30);
    newOffice1.name="新办公楼1";
    scene.add(newOffice1); 
  
    let newOffice2 = tempOffice.clone();      
    newOffice2.translateZ(105); //先移动在旋转
    newOffice2.translateX(100); 
    newOffice2.rotateY(Math.PI/2)
    //newOffice2.translateX(-270);//先旋转再移动
    //newOffice2.translateZ(100);
    //newOffice2.position.set(250,0,30); //或直接设置位置
  
    newOffice2.scale.set(1.5, 1, 1.5) 
    newOffice2.name="新办公楼2";
    scene.add(newOffice2); 
  
    newOffice2.updateMatrix();
    console.log('当前矩阵:', newOffice2.matrix);
    console.log('局部坐标(移动后):', newOffice2.position);
    newOffice2.getWorldPosition(worldPosition);
    console.log('全局坐标(移动后):', worldPosition);
  

  运行结果：
  

  左边只是克隆平移。右边克隆、平移、旋转、缩放。
  打印结果：

    当前矩阵:  -3.33e-16, 0,  -1.5000000000000004, 0,
               0, 1,0, 0,
              1.5, 0, -3.3306690738754696e-16, 0,
              250, 0,30, 1
    全局坐标(移动前): Object { x: 250, y: 0, z: 30 }
    局部坐标(移动后): Object { x: 250, y: 0, z: 30 }
  

  📍当前矩阵也可以在 threejs场景->新办公楼2->matrix中查看。

• 在 Three.js 中，Object3D.matrix 是一个 4x4 变换矩阵，通常包含以下变换（按计算顺序排列）：

1. 完整矩阵结构

一个典型的 matrix.elements 数组（列主序）：

 [
  m11, m12, m13, m14,  // 旋转/缩放 (X轴基向量 + 位移X)
  m21, m22, m23, m24,  // 旋转/缩放 (Y轴基向量 + 位移Y)
  m31, m32, m33, m34,  // 旋转/缩放 (Z轴基向量 + 位移Z)
  m41, m42, m43, m44   // 通常为 [0, 0, 0, 1]（齐次坐标）
 ]

2. 主要变换成分

   变换类型	矩阵区块	说明
   缩放 (Scale)	左上 3x3 的对角线	[scaleX, 0, 0], [0, scaleY, 0], [0, 0, scaleZ]
   旋转 (Rotation)	左上 3x3 的非对角线	由旋转后的基向量组成（受四元数 quaternion 或欧拉角 rotation 控制）
   平移 (Translation)	最后一行	[0, 0, 0, 1]（齐次坐标的标准设置）

📍齐次坐标是一种用于表示几何点的坐标系统。以三维物体上的点（1，5，6）为例，它原本有XYZ三个坐标。若要使该点发生位置变化，需引入齐次坐标，将其表示为（1，5，6，1）。这可以理解为四维空间在三维空间的一个投影。

3. 完整矩阵结构

   元素	说明	典型值	元素	说明	典型值
   m11	X轴基向量X (缩放/旋转)	scaleX/1.0	m31	Z轴基向量X (旋转)	0.0
   m12	X轴基向量Y (旋转)	0.0	m32	Z轴基向量Y (旋转)	0.0
   m13	X轴基向量Z (旋转)	0.0	m33	Z轴基向量Z (缩放/旋转)	scaleZ/1.0
   m14	平移X	translateX	m34	平移Z	translateZ
   m21	Y轴基向量X (旋转)	0.0	m41	齐次坐标	标准为0
   m22	Y轴基向量Y (缩放/旋转)	scaleY/1.0	m42	齐次坐标	标准为0
   m23	Y轴基向量Z (旋转)	0.0	m43	齐次坐标	标准为0
   m24	平移Y	translateY	m44	齐次坐标	顶点为1向量为0

将打印结果优化一下，优化浮点误差（-3.33e-16≈0 的项视为 0，1.5000000000000004 ≈ 1.5）：

 [
  -3.33e-16, 0,  -1.5, 0, ->  0, 0,-1.5, 0,(m11, m21, m31, m41) -> 行列转换  0, 0,1.5,250,(m11, m12, m13, m14)
     0, 1,0, 0,               0, 1,   0, 0,(m12, m22, m32, m42)             0, 1,  0,  0,(m21, m22, m23, m24)
 1.5, 0, -3.33e-16, 0,      1.5, 0,   0, 0,(m13, m23, m33, m43)          -1.5, 0,  0, 30,(m31, m32, m33, m34)
  250, 0,30, 1              250, 0,  30, 1 (m14, m24, m34, m44)             0, 0,  0,  1 (m41, m42, m43, m44)
 ]
   

1. 🏷️提取平移（Translation），平移信息直接来自矩阵的最后一列（m14, m24, m34），结果：（ 250, 0, 30）,对应代码：newOffice2.position.set(250,0,30)
2. 🏷️提取缩放（Scale），结果：（1.5, 1, 1.5） 对应代码：newOffice2.scale.set(1.5, 1, 1.5)

💠X 轴缩放（第 1 列）：
$$\sqrt{0^2+0^2+(-1.5{)}^2}=1.5$$
💠Y 轴缩放（第 2 列）：
$$\sqrt{0^2+1^2+0^2}=1$$
💠Z 轴缩放（第3列）：
$$\sqrt{1.5^2+0^2+0^2}=1.5$$

3. 🏷️提取旋转（Rotation）
   💠X 轴方向（第 1 列 [0, 0, -1.5]）→ 归一化 [0, 0, -1] ⭕X轴变为-Z轴方向
   💠Y 轴方向（第 2 列 [0, 1, 0]）→ 归一化 [0, 1, 0] ⭕Y轴不变
   💠Z 轴方向（第 3 列 [1.5, 0, 0]）→ 归一化 [1, 0, 0] ⭕ Z轴变为X轴正方向
   结果：从Y正方向看原点，逆时针旋转90°,对应代码：newFactory2.rotateY(Math.PI/2)
   

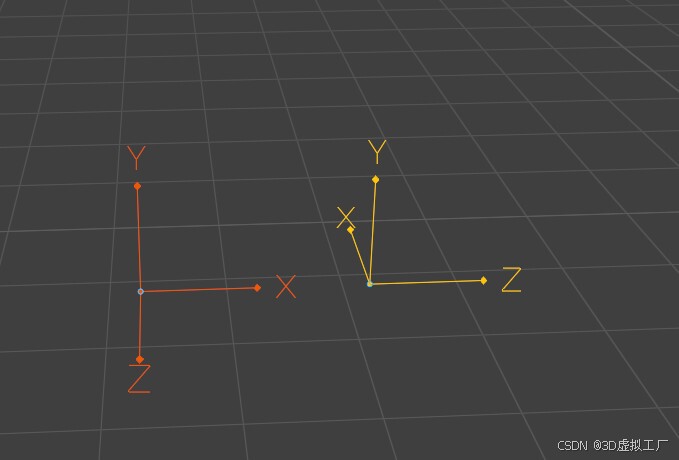
如果先旋转再移动

  //newOffice2.translateZ(105); 
  //newOffice2.translateX(100); 
  newOffice2.rotateY(Math.PI/2)
  newOffice2.translateX(-105);//原本向Z移动105就得向X移动-105
  newOffice2.translateZ(100);//原本向X移动100就得向Z移动100

• 最后验证矩阵转换结果：Blender局部坐标（31, -9, 25.5）变换为three.js局部坐标（31, 25.5, 9）。如需了解具体转换方法，请参考三维坐标系说明。
  

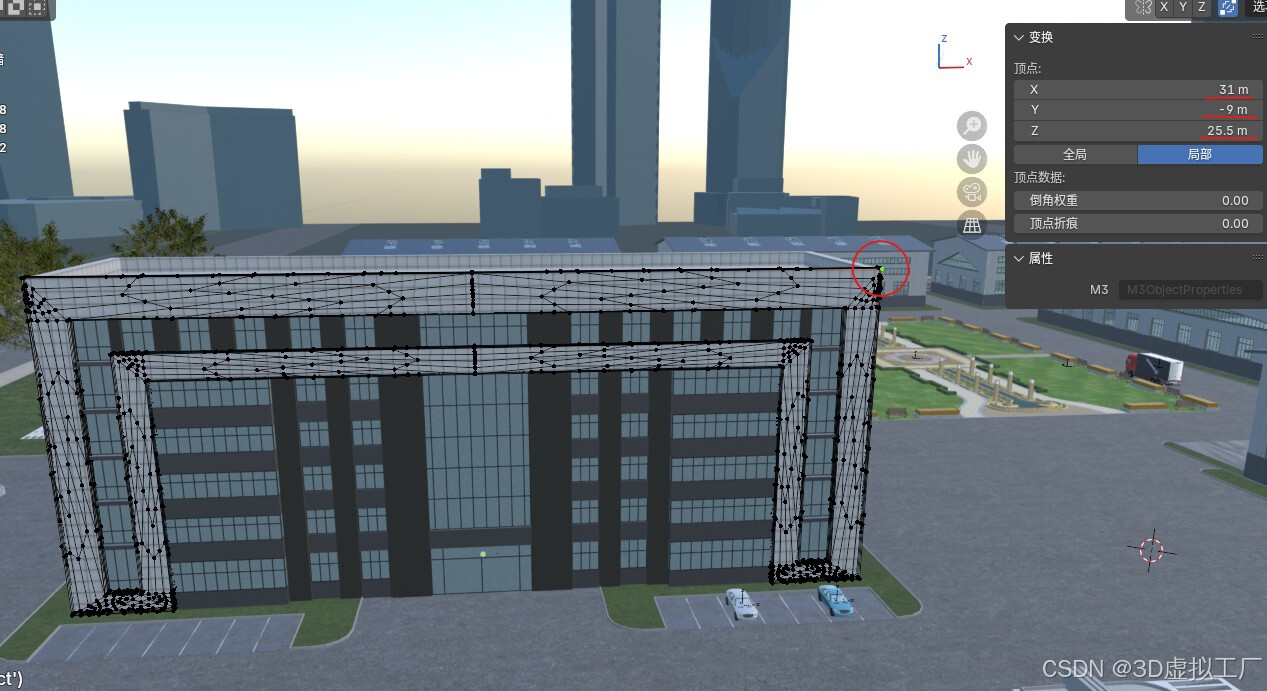
• 给定变换矩阵：
  $$M=\left[\begin{array}{cccc}0& 0& 1.5& 250\\ 0& 1& 0& 0\\ -1.5& 0& 0& 30\\ 0& 0& 0& 1\end{array}\right]$$

• 顶点：
  $$v=(31,25.5,9,1)$$

• 计算步骤
  $$v^{\prime }=M\ast v=\left[\begin{array}{c}0\ast 31+0\ast 25.5+1.5\ast 9+250\ast 1\\ 0\ast 31+1\ast 25.5+0\ast 9+0\ast 1\\ -1.5\ast 31+0\ast 25.5+0\ast 9+30\ast 1\\ 0\ast 31+0\ast 25.5+0\ast 9+1\ast 1\end{array}\right]$$

• 逐项计算：

  • $v_x^{\prime }$:
    $$0+0+13.5+250=263.5$$

  • $v_y^{\prime }$:
    $$0+25.5+0+0=25.5$$

  • $v_z^{\prime }$:
    $$-46.5+0+0+30=-16.5$$

  • $v_w^{\prime }$:
    $$0+0+0+1=1$$

• 最终结果
  变换后的顶点坐标为：
  $$(263.5,25.5,-16.5,1)$$
  转换为blender坐标就是：
  $$(263.5,16.5,25.5,1)$$
  

• 点击【专栏目录】查看专栏其他内容。