1️⃣2️⃣three.js_物体的镜像

12、物体的镜像

• 3D虚拟工厂在线体验

12.1、克隆镜像的另一半

• 镜像（Mirror Reflection）是指物体相对于某个参考平面或坐标轴进行对称变换的操作。
  

• 在父级坐标系中，物体镜像变换的数学本质是对指定轴向的坐标值进行取反操作。

   //先定位货车左边
   const tempScene = scene.children.find(t => t.name == 'Scene')
   const tempTruck = tempScene.children.find(t => t.name == 'Truck');//父级，空物体
   const tempTruckLeft = tempTruck.children.find(t => t.name == 'TruckLeft'); //货车左边
   //克隆出货车右边
   const newTruck1Right= tempTruckLeft.clone() 
   newTruck1Right.name = 'TruckRight'
   //矩阵镜像变换
   const mirrorMatrix = new THREE.Matrix4().makeScale(-1, 1, 1); 
   newTruck1Right.applyMatrix4(mirrorMatrix)
   newTruck1Right.updateMatrix();
   console.log('当前矩阵:', newTruck1Right.matrix);
   //newTruck1Right.translateX(3)
   tempTruck.add(newTruck1Right)
  

• 现实世界中广泛存在对称结构的物体（如人体、车辆、建筑等）。通过镜像变换技术，可以高效生成对称部分，不仅能大幅降低建模工作量，还能有效优化模型存储空间。
  

• 镜像前矩阵与镜像后矩阵对比（如需了解矩阵，请参考物体的平移、缩放、旋转说明 ）
  $$M=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]M=\left[\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

• 任意一顶点：
  $$v=(2,5,6,1)$$

• 计算步骤
  $$v^{\prime }=M\ast v=\left[\begin{array}{c}-1\ast 2+0\ast 5+0\ast 6+0\ast 1\\ 0\ast 2+1\ast 5+0\ast 6+0\ast 1\\ 0\ast 2+0\ast 5+1\ast 6+0\ast 1\\ 0\ast 2+0\ast 5+0\ast 6+1\ast 1\end{array}\right]=\left[\begin{array}{c}-2\\ 5\\ 6\\ 1\end{array}\right]$$

• 从变换结果可以看出，关键代码 mirrorMatrix = new THREE.Matrix4().makeScale(-1, 1, 1); 使得物体在X轴方向的坐标值发生了符号反转。

• 🛑需要特别注意的是，货车的镜像变换是在父级坐标系（空物体坐标系）下进行的，其变换效果是使货车相对于父级坐标原点的X轴坐标值发生符号反转。

12.2、物体镜像变换

• 物体经过镜像变换后，其原有的空间关系会发生对调。例如，若原始物体一侧为墙、另一侧为窗户，镜像后二者的左右位置将完全互换。

• 在涉及复合变换（如平移、旋转和镜像同时操作）的项目需求中，理清父级坐标系的层级关系就显得尤为重要。

  const tempScene = scene.children.find(t => t.name == 'Scene')
  const tempDoor = tempScene.children.find(t => t.name == '门卫');
  const tempDoorSouth = tempDoor.children.find(t => t.name == '门卫室南');  
  const newDoor= tempDoorSouth.clone() 
  newDoor.translateX(30);
  newDoor.translateZ(15); 
  const mirrorMatrix = new THREE.Matrix4().makeScale(-1, 1, 1); //x轴镜像
  newDoor.applyMatrix4(mirrorMatrix) 
  newDoor.rotateY(-Math.PI/2) //顺时针旋转90度 
  tempDoor.add(newDoor)
  

• 在常规认知中，首先定位到门卫室南，沿X轴平移30米，沿Z轴平移15米，应用镜像变换，顺时针旋转90度。然而，实际执行结果与预期不符：
  

• ❓❓❓右侧箭头处是预期位置，红圈⭕为父级坐标系原点。实际X轴移动了-30米（与预期相反），旋转方向也变为逆时针90度（与预期顺时针相反）。

• 下面比较烧脑，谨慎观看！
  

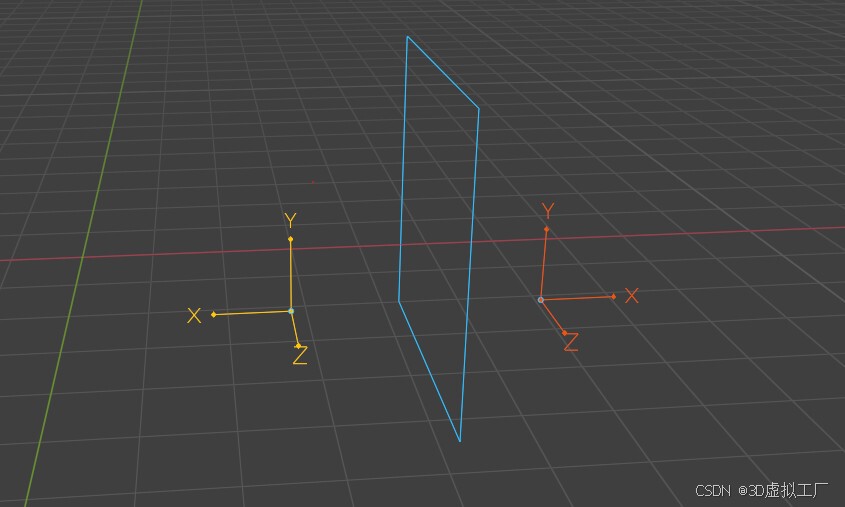
• 由于父级坐标系原点必须保持固定，因此我们首先在初始坐标系下执行镜像变换。
  

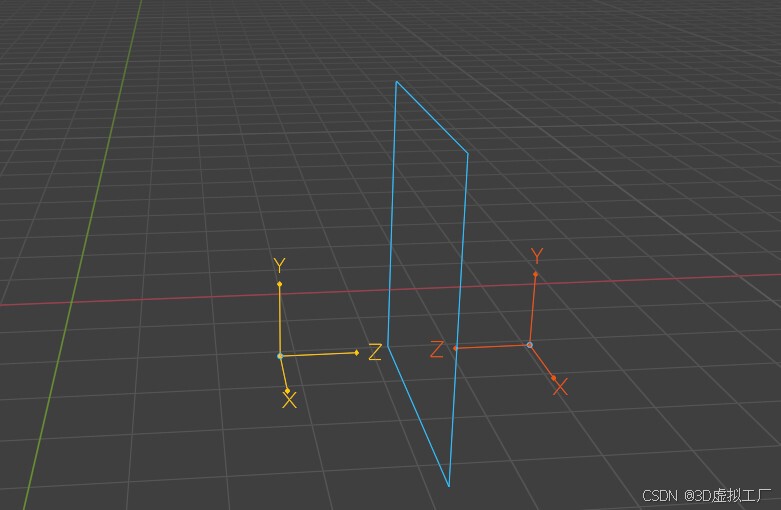
• 在镜像变换后的坐标系中，现实世界中的顺时针90度旋转，将对应表现为镜像中逆时针90度旋转
  

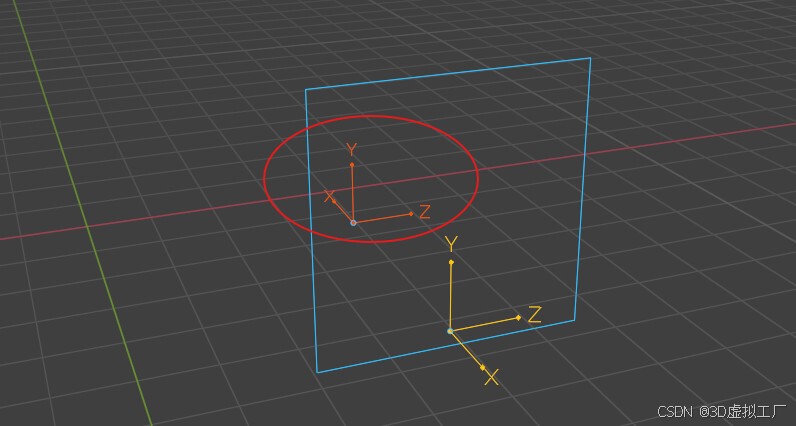
• 最终，将镜子旋转至X轴方向，得到红圈标记的坐标系。随后执行以下平移操作：Z轴平移30米，X轴平移-15米。
  根据上述分析，代码修正如下：

  const tempScene = scene.children.find(t => t.name == 'Scene')
  const tempDoor = tempScene.children.find(t => t.name == '门卫');
  const tempDoorSouth = tempDoor.children.find(t => t.name == '门卫室南');  
  const newDoor= tempDoorSouth.clone() 
  
  const mirrorMatrix = new THREE.Matrix4().makeScale(-1, 1, 1); //x轴镜像
  newDoor.applyMatrix4(mirrorMatrix) 
  newDoor.rotateY(Math.PI/2) //逆时针旋转90度 
  
  newDoor.translateZ(30);
  newDoor.translateX(-15); 
  tempDoor.add(newDoor)
  

  ✅执行结果：

• 图中看到，X轴移动30米，Z轴移动15米，顺时针旋转90度，应用了X镜像，窗户朝东开，符合预期。

• 点击【专栏目录】查看专栏其他内容。