Audio processing in TensorFlow

文章来自

Author ：Dario Cazzani

原文网站：链接

 

未翻译...

An implementation of the Short Time Fourier Transform

I found audio processing in TensorFlow hard, here is my fix

There are countless ways to perform audio processing. The usual flow for running experiments with Artificial Neural Networks in TensorFlow with audio inputs is to first preprocess the audio, then feed it to the Neural Net.

What happens though when one wants to perform audio processing somewhere in the middle of the computation graph?
TensorFlow comes with an implementation of the Fast Fourier Transform, but it is not enough.

In this post I will explain how we implemented it and provide the code so that the Short Time Fourier Transform can be used anywhere in the computation graph.

The code

All the code is available on my GitHub: Audio Processing in Tensorflow.
Feel free to add your contribution there.

Audio preprocessing: the usual approach

When developing a Speech Recognition engine using Deep Neural Networks we need to feed the audio to our Neural Network, but… what is the right way to preprocess this input?

There are 2 common ways to represent sound:

• Time domain: each sample represents the variation in air pressure.
• Frequency domain: at each time stamp we indicate the amplitude for each frequency.

Despite the fact that Deep Neural Networks are extremely good at learning features automagically, it is always a good idea to rely on known features that carry the information needed for the task that we are trying to solve.

For most application, a Speech Recognition Engine included, the features we are interested in are encoded in the frequency domain representation of the sound.

The spectrogram and the Short Time Fourier Transform

A spectrogram shows how the frequency content of a signal changes over time and can be calculated from the time domain signal.
The operation, or transformation, used to do that is known as the Short Time Fourier Transform.

I could let the Neural Network figure out how to learn this operation, but it turns out to be quite complex to learn with 1 hidden layer. (refer to the Universal approximation theorem)

I could add more layers, but I want to keep the complexity of the Neural Networks as small as possible and learn features only where it is most needed.

I have used the example of developing an Automatic Speech Recognition engine, but the use of the spectrogram as input to Deep Neural Nets is common also for similar tasks involving non-speech audio like noise reduction, music genre classification, whale call detection, etc.

A particular project that I want to mention is Magenta, from the Google Brain team, who’s aim is to advance the state of the art in machine intelligence for music and art generation.

Why TensorFlow?

I mainly use TensorFlow when implementing Artificial Neural Networks and, because I haven’t found an implementation of the Short Time Fourier Transform in TF, I decided to implement our own.
[edit: June 4th 2018] — since TensorFlow 1.3 they added some useful DSP functionalities.

There can also be multiple reasons why a deep learning practitioner might want to include the Short Time Fourier Transform (STFT for my friends) in the computation graph, and not just as a separate preprocessing step.

Keep in mind that I haven’t focused on making this efficient. It should (and will) be improved before being used in production.

What you need to know

In order to understand how the STFT is calculated, you need to understand how to compute the Discrete Fourier Transform.

Discrete Fourier Transform — DFT

This part can appear quite technical for those who are not familiar with these concepts, but I think it is important to go through some maths in order give a complete understanding of the code.

Theory
Fourier analysis is fundamentally a method for expressing a function as a sum of periodic components, and for recovering the function from those components. When both the function and its Fourier transform are replaced with discretized counterparts, it is called the discrete Fourier transform (DFT).

Given a vector x of n input amplitudes such as:

{x[0], x[1], x[2], x[3], …, x[N-1]}

the Discrete Fourier Transform yields a set of n frequency magnitudes.

The DFT is defined by this equation:

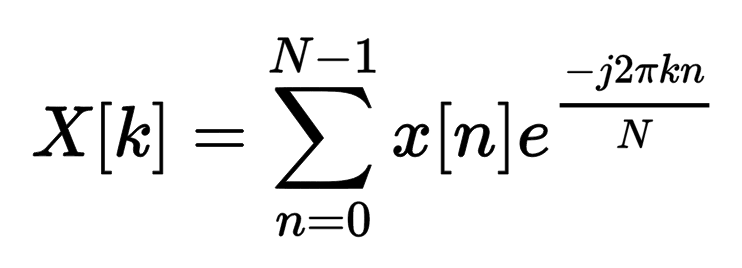
                                      DFT equation

• k is used to denote the frequency domain ordinal
• n is used to represent the time-domain ordinal
• N is the length of the sequence to be transformed.

Fast Fourier Transform
The Fast Fourier Transform is an efficient implementation of the DFT equation. The signal must be restricted to be of size of a power of 2.

This explains why N (the size of the signal in input to the DFT function) has to be power of 2 and why it must be zero-padded otherwise.

One can detect whether x is a power of 2 very simply in python:

def is_power2(x):
    return x > 0 and ((x & (x - 1)) == 0)

We only need half of it
Real sine waves can be expressed as the sum of complex sine waves using Euler’s identity

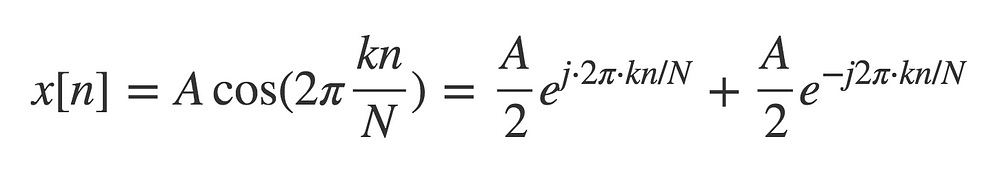
Because the DFT is a linear function, the DFT of a sum of sine waves is the sum of the DFT of each sine wave. So for the spectral case you get 2 DFTs, one for the positive frequencies and one for the negative frequencies, which are symmetric.
This symmetry occurs for real signals that can be viewed as an infinite (or finite in our case) sum of sine waves.

Windowing
Truncating a signal in the time domain will lead to ripples appearing in the frequency domain.
This can be understood if you think of truncating the signal as if you applied a rectangular window. Applying a window in the time domain results in a convolution in the frequency domain.
The ripples are caused when we convolve the 2 frequency domain representations together.

Find out more about spectral_leakage if you’re interested.

Here is an example of an implementation of windowing in Python:

from scipy.signal import hanning
import tensorflow as tf
import numpy as np

N = 256 # FFT size
audio = np.random.rand(N, 1) * 2 - 1
w = hanning(N)

input  = tf.placeholder(tf.float32, shape=(N, 1))
window = tf.placeholder(tf.float32, shape=(N))
window_norm = tf.div(window, tf.reduce_sum(window))
windowed_input = tf.multiply(input, window_norm)

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    windowed_input_val = sess.run(windowed_input, {
        window: w,
        input: audio
    })

 

Zero-phase padding

In order to use the FFT, the input signal has to have a power of 2 length. If the input signal does not have the right length, zeros can be appended to the signal itself both at the beginning and at the end.
Because the zero sample is originally at the center of the input signal, I split the padded signal through the middle and swap the order of these 2 parts.

The next code snippet shows how to do this in TensorFlow for a batch of inputs:

N = 512 # FFT size
input_length = int(input.get_shape()[1])

zeros_left = tf.zeros([int(input.get_shape()[0]), int((N - input_length+1) / 2)])
zeros_right = tf.zeros([int(input.get_shape()[0]), int((N - input_length) / 2)])
input_padded = tf.concat([zeros_left, input, zeros_right], axis=1)

fftbuffer_left  = tf.slice(windowed_input, [0, int(N/2)], [-1, -1])
fftbuffer_right = tf.slice(windowed_input, [0, 0],   [-1, int(N/2)])
fftbuffer = tf.concat([fftbuffer_left, fftbuffer_right], axis=1)

FFT, Magnitude and Phase
You now have everything you need to calculate the magnitude of the spectrogram in decibels and the phase of the signal:

fft = tf.fft(tf.cast(fftbuffer, tf.complex64))

# compute absolute value of positive side
sliced_fft = tf.slice(fft, [0, 0], [-1, positive_spectrum_size])
abs_fft = tf.abs(sliced_fft)

# magnitude spectrum of positive frequencies in dB
magnitude = 20 * log10(tf.maximum(abs_fft, 1E-06))

# phase of positive frequencies
phase = angle(sliced_fft)

Short Time Fourier Transform

You now know how to compute the DFT to evaluate the frequency content of a signal.
The STFT is used to analyze the frequency content of signals when that frequency content varies with time.
You can do this by:

1. Taking segments of the signal.
2. Windowing those out from the rest of the signal, and applying a DFT to each segment.
3. Sliding this window along each segment.

You get DFT coefficients as a function of both time and frequency.

The complete code is divided in 2 parts: helpers.py and stft.py.

"""
Authors:    Dario Cazzani
"""
#!/usr/bin/python
from __future__ import division
import tensorflow as tf
import numpy as np

def log10(x):
    num = tf.log(x)
    den = tf.log(tf.constant(10, dtype=num.dtype))
    return(tf.div(num, den))

def overlapping_slicer_3D(_input, block_size, stride):
    _input_rank = int(len(_input.get_shape()))
    blocks = []
    n = _input.get_shape().as_list()[_input_rank-1]
    low = range(0, n, stride)
    high = range(block_size, n+1, stride)
    low_high = zip(low, high)
    for low, high in low_high:
	blocks.append(_input[:, low:high])
    return(tf.stack(blocks, _input_rank-1))

def angle(z):
    if z.dtype == tf.complex128:
        dtype = tf.float64
    elif z.dtype == tf.complex64:
        dtype = tf.float32
    else:
        raise ValueError('input z must be of type complex64 or complex128')
        
    x = tf.real(z)
    y = tf.imag(z)
    x_neg = tf.cast(x < 0.0, dtype)
    y_neg = tf.cast(y < 0.0, dtype)
    y_pos = tf.cast(y >= 0.0, dtype)
    offset = x_neg * (y_pos - y_neg) * np.pi
    return tf.atan(y / x) + offset

def is_power2(x):
    return x > 0 and ((x & (x - 1)) == 0)

"""
Authors:    Dario Cazzani
"""
#!/usr/bin/python
from __future__ import division
import tensorflow as tf
from helpers import log10, is_power2, angle, overlapping_slicer_3D

def dft_analysis(_input, window, N):
	"""
	Analysis of a signal using the discrete Fourier transform
	inputs:
	_input: tensor of shape [batch_size, N]
	window: analysis window, tensor of shape [N]
	N: FFT size
	returns:
	Tensors m, p: magnitude and phase spectrum of _input
	m of shape [batch_size, num_coefficients]
	p of shape [batch_size, num_coefficients]
	"""

	if not(is_power2(N)):
		raise ValueError("FFT size is not a power of 2")

	_, input_length = _input.get_shape()
	_input_shape = tf.shape(_input)

	if (int(input_length) > N):
		raise ValueError("Input length is greater than FFT size")

	if (int(window.get_shape()[0]) != N):
		raise ValueError("Window length is different from FFT size")

	if int(input_length) < N:
		with tf.name_scope('DFT_Zero_padding'):
			zeros_left = tf.zeros(_input_shape)[:, :int((N - (int(input_length))+1) / 2)]
			zeros_right = tf.zeros(_input_shape)[:, :int((N - (int(input_length))) / 2)]
			_input = tf.concat([zeros_left, _input, zeros_right], axis=1)
			assert(int(_input.get_shape()[1]) == N)

	positive_spectrum_size = int(N/2) + 1
	with tf.name_scope('Windowing'):
		window_norm = tf.div(window, tf.reduce_sum(window))
		# window the input
		windowed_input = tf.multiply(_input, window_norm)

	with tf.name_scope('Zero_phase_padding'):
		# zero-phase window in fftbuffer
		fftbuffer_left  = tf.slice(windowed_input, [0, int(N/2)], [-1, -1])
		fftbuffer_right = tf.slice(windowed_input, [0, 0],   [-1, int(N/2)])
		fftbuffer = tf.concat([fftbuffer_left, fftbuffer_right], axis=1)
		fft = tf.spectral.rfft(fftbuffer)

	with tf.name_scope('Slice_positive_side'):
		sliced_fft = tf.slice(fft, [0, 0], [-1, positive_spectrum_size])

	with tf.name_scope('Magnitude'):
		# compute absolute value of positive side
		abs_fft = tf.abs(sliced_fft)

		# magnitude spectrum of positive frequencies in dB
		magnitude = 20 * log10(tf.maximum(abs_fft, 1E-06))

	with tf.name_scope('Phase'):
		# phase of positive frequencies
		phase = angle(sliced_fft)

	return magnitude, phase

def stft_analysis(_input, window, N, H) :
	"""
	Analysis of a sound using the short-time Fourier transform
	Inputs:
	_input: tensor of shape [batch_size, audio_samples]
	window: analysis window, tensor of shape [N]
	N: FFT size, Integer
	H: hop size, Integer
	Returns:
	magnitudes, phases: 3D tensor with magnitude and phase spectra of shape
	[batch_size, coefficients, frames]
	"""
	if (H <= 0):
		raise ValueError("Hop size (H) smaller or equal to 0")
	if not(is_power2(N)):
		raise ValueError("FFT size is not a power of 2")

	_input_shape = tf.shape(_input)
	pad_size = int(N / 2)
	with tf.name_scope('STFT_Zero_padding'):
		zeros_left = tf.zeros(_input_shape)[:, :pad_size]
		zeros_right = tf.zeros(_input_shape)[:, :pad_size]
		_input = tf.concat([zeros_left, _input, zeros_right], axis=1)

	with tf.name_scope('overlapping_slicer'):
		sliced_input = overlapping_slicer_3D(_input, N, H)
	_, frames, _ = sliced_input.get_shape()

	with tf.name_scope('DFT_analysis'):
		reshaped_sliced_input = tf.reshape(sliced_input, (-1, N))
		m, p = dft_analysis(reshaped_sliced_input, window, N)

	with tf.name_scope('STFT_output_reshape'):
		magnitudes = tf.reshape(m, (-1, int(m.get_shape()[-1]), int(frames)))
		phases =     tf.reshape(p, (-1, int(p.get_shape()[-1]), int(frames)))

	return magnitudes, phases

Conclusion

The possibility of doing the STFT in TensorFlow allows Machine Learning practitioners to perform the transformation of a signal, from time-domain to frequency domain, anywhere in the computation graph.
New tools always bring new ideas and we hope this post will be the source of new ideas for developing new Deep Learning solutions.

音频相关文章的搬运工，如有侵权 请联系我们删除。

微博：砖瓦工-日记本

联系方式qq:1657250854