线性代数之行列式基础点

                                      线性代数之行列式基础点

顺序和逆序

如果我们定义一个排列的每个元素从左到右按照递增的顺序的摆放的，就称这样的排列是顺序的。比如3个数字组成的数列1 2 6，数列的第二个元素比第一个大，第三个比第二个大。那么相反的如果从左到右不是递增的，则为称之为逆序的。比如1 6 2，这里第三个不比第二大，所以是个逆序。

逆序数：给定一个数列，针对数列里每个数字计算出它的逆序个数（即它左边比它大的个数）的总和，则称之为逆序数。

注：当然也可以数右边比它小的个数。

令逆序数为为t，则

=

逆序数是奇数的排列叫做奇排列，逆序数是偶数的排列叫做偶排列。

数列的对换

把排列里任意两个元素对换（交换）形成新排列的动作叫做对换，特别的如果两个元素是相邻的，就叫做相邻交换。

不难发现:

1 任何一个交换都可以由相邻交换得到

2 两个元素交换后排列的奇偶性发生改变，即以前是偶排列会变成奇排列。

3 奇排列变成自然（标准）排列需要奇数次，同理偶排列需要偶数次。

 

三阶行列式

 =

这里实际上每行每列取不同时同行同列的一个数得到元素乘积的累加和。根据组合的规律不难发现共有6种，即。

这里不难发现：

1. 1行列式是n×n的，即有n行n列，有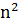个数。或者说它是方的
2. 行列式以||的形式表示，它本质上是一个数
3. 行列式的阶数即是行列式的行数或者列数

3阶行列式通用表示方法是:

其中t是每个排列p1p2p3的逆序数， 

是所有以行按照1、2、3排列，列按照p1、p2、p3排列的元素组合的乘积，此时再乘以 以确定且正负性。而∑是对所有的求和。

 

注：

1.  这里p1、p2、p3都可能会取到1、2、3但排列时不能重复。
2. 如果p1=3、p2=1、p3=2则 = 因为这里t=0+1+1=2。
3.  

也可以表示成或者

 

N阶行列式

有了3阶行列式的定义不难推广到一般的情况，对于N阶行列式，可以类似的定义出。

 

==

 注：因为乘法满足结合律，所以这里的也可以不按照行(列)的自然（标准）顺序来排序。

行列式的性质

1.  行列式转置值不变
2.  行列式兑换两行（列）值变号
3. 如果行列式里两行（列）完全相同，则行列式等于0
4. 如果行列式的某行都乘以一个数k，等于k乘以该行列式源于乘法的提取公因子，因为某一列乘以一个数k，则组合式 有因子k。k等于0时亦成立。
5. 行列式的某一行（列）有公因子k，则可以表示成k乘新行列式（对应元素除以k），即k可以提到行列式的外面。
6. 如果行列式里两行（列）成比例，则行列式等于0.源于性质5和性质3
7. 如果行列式里某行（列）是两个数相加，则该行列式可分成两个行列式的和（新行列式的组合方式是将该行或者列拆成两个数，其它的行或列保持不变）。 源于乘法的分配律和组合律。
8. 行列式里某一行（列）乘以数k加到另一行（列）上后行列式的值不变。

 

几种特殊的行列式

主对角线行列式是主对角线（从左上角到右下角的斜线）元素不全为0，其余元素都为0的行列式。

次对角线行列式是主对角线（从右上角到左下角的斜线）元素不全为0，其余元素都为0的行列式。

上三角行列式是主对角线以下全为0的行列式，又简称上三角。

下三角行列式是主对角线以上全为0的行列式，又简称下三角。

对称行列式是aij=aji 即行列式里下标行列互换处的元素也对应相等。

行列式的展开式

余子式：将元素aij对应的第i行和第j列去掉之后组成的n-1阶行列式叫做的余子式。

代数余子式：Aij =叫做aij的代数余子式。

行列式的值等于某一行(列)的各个元素与其对应的代数余子式的乘积之和，即

D =   (i=1,2,…,n),

或者

D=   (j=1,2,…,n),

余子式、代数余子式的求法示例: 比如有行列式A

1  2  3

4  5  6

7  8  9

M11

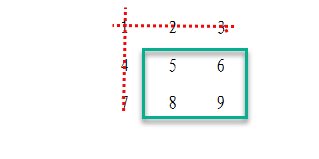
A11 =   

 同理

M12

A12 =  

范德蒙行列式

特别的针对行列式里每列的每行是上一行的k倍时的行列式,它的值等于如下：

注：

1. 该数针对每列一般不同
2. 该数一般是第二行里的数
3. 第一行的数一般都是1

 

克莱姆法则

针对如上的方程，可以借助行列式得出其解：

其中

那么该方程有唯一解，且

其中D1 是将方程组右边的按顺序依次替换行列式D第一列里的元素而组成的新行列式。依此类推。