前言
本文讲以下四种空间
- 标量空间;
- 向量空间(vector space 或者线性空间 linear space);
- 仿射空间(affine space);
- 欧几里得空间(Euclidean space);
简单来说,标量空间里只有标量,向量空间中除了标量还有向量。而仿射空间比向量空间引入了点。欧几里得空间引入了距离的概念,严格意义上的欧几里得空间包括标量,向量,不过仿射空间中的点的概念也可以引入欧几里得空间中。
本文主要讲述后三种空间中包含的元素(数学对象,比如向量),以及在这些元素之间定义的运算。重点讲仿射空间以及欧几里得空间, 以及这两个空间分别对应的齐次坐标系以及欧几里得坐标系。
在具体展开之前,我先说说标架(frame)以及坐标系(coordinate)之间的关系,我时常纠结这些概念之间有什么不同,稍微查了查,坐标系是理论上的概念,而标架是具体的概念,“对于标架的一个不太严谨的说法,他是一个原点固定在某处的向量坐标系”。也就是说,当我讨论坐标系的时候,可以认为我在讨论某一种水果,比如我在讨论苹果有什么性质,但是当我说标架的时候,就好比我在说某个具体的苹果的性质了。不过在我遇到的大部分情况都完全没必要严格区分这两个概念。本文也不需要。
标量空间
标量空间这里就不多说了,改空间只有一个数学对象,那就是标量。定义的运算有加法和乘法(减法和除法分别是加法和乘法的逆元)。标量是只有大小没有方向的量,我不说你们也知道。
向量空间
包括的数学对象:
- 标量
- 向量: 向量就是既有大小又有方向的量(定义)。一般用黑斜体小写字母表示,如: u u u, v v v, w w w
包含的运算:
- 向量-向量加法
- 标量-向量乘法
向量空间的其他概念
-
线性:
其实是两个性质的和.注意线性其实指线性变换或者说线性映射,本质上是一种函数.
线性(变换) = 齐次性 + 可加性.
可加性(Additivity): f ( x + y ) = f ( x ) + f ( y ) f(x+y) = f(x) + f(y) f(x+y)=f(x)+f(y)
齐次性(同质性 Homogeneity): n f ( x ) = f ( n x ) , n ∈ R nf(x) = f(nx) , n \in R nf(x)=f(nx),n∈R
我们可以举个例子:
与矩阵相乘是线性变换吗?
设 a , b 是 向 量 , n 是 实 数 , M 是 矩 阵 设a ,b 是向量, n是实数, M是矩阵 设a,b是向量,n是实数,M是矩阵
M ∗ ( a + b ) = M ∗ a + M ∗ b (1) M* (a + b) = M*a +M*b \tag{1} M∗(a+b)=M∗a+M∗b(1)
n ∗ M ∗ a = M ∗ ( n ∗ a ) (2) n* M*a = M *(n*a) \tag{2} n∗M∗a=M∗(n∗a)(2)
由(1)(2)可得乘以一个矩阵的运算是线性变换. -
线性相关:(暂时懒得写)
-
基和维数:(暂时懒得写)
仿射空间
向量空间没有位置的概念, 因此向量空间并不能表述几何物体, 故需要用到仿射空间.
包括的数学对象:
- 标量
- 向量: 向量就是既有大小又有方向的量(定义)。一般用黑斜体小写字母表示,如: u u u, v v v, w w w
- 点(原点)
具体什么意思呢,比如说我们用三个两两正交(垂直)的单位向量 i , j , z i,j,z i,j,z 作为三维向量空间的基,
我们可以记 该三维向量空间为
V = { i , j , z } V = \{ i , j, z\} V={i,j,z}
如果在这是三个单位基向量的基础上再引入一个基, 但这个基是一个点,记为 O O O,
A = { i , j , z , O } A = \{ i , j, z , O\} A={i,j,z,O}
具体后面讲齐次坐标系的时候会更清楚.
先说包含的运算:
- 向量-向量加法
- 标量-向量乘法
- 点-向量加法
- 点-点减法
具体来说:
点-向量加法得到一个点
点-点减法得到一个向量
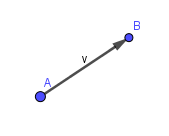
如上图所示: A + v = B ; B − A = v A + v = B ; B - A = v A+v=B;B−A=v
一个向量的起点加上该向量得到该向量的终点, 一个向量的终点减去起点得到该向量。
另外还有一种运算叫仿射加法(affine addition):
因为仿射空间定义了标量数乘以及点向量加法,因此可以有:
$Q = P + nv, n\in R $ 且 $ v = R - P$
则
Q
=
P
+
n
(
R
−
P
)
=
(
1
−
n
)
P
+
n
R
Q = P + n(R-P) = (1-n)P + nR
Q=P+n(R−P)=(1−n)P+nR
也可以写成
Q
=
a
1
P
+
a
2
R
,
其
中
a
1
+
a
2
=
1
Q = a_1P + a_2R, 其中a_1 + a_2 = 1
Q=a1P+a2R,其中a1+a2=1
仿射加法的形式好像定义了点-点加法。但本质上是点-向量加法,点-点减法以及数乘的结合。
齐次坐标系
这里建议大家在已经知道欧氏坐标系的基础上再来看齐次坐标系。(已经知道欧式坐标系的不必去看,其实欧式坐标系简单来说,三维的欧式坐标系就是我们高中常见的xyz坐标系。)
前面我说了:
三维向量空间可为
V
=
{
i
,
j
,
z
}
V = \{ i , j, z\}
V={i,j,z}
三维仿射空间可以记为
A
=
{
i
,
j
,
z
,
O
}
A = \{ i , j, z , O\}
A={i,j,z,O}
大家都知道三维空间(严格说是三维欧式空间)中一个向量表示为
v
v
v = (a,b,c) ,即
v
v
v = a$i + $ b
j
+
j +
j+c
z
z
z
那么在三维仿射空间中的一个数学对象
o
b
j
e
c
t
=
object=
object= a$i + $ b
j
+
j +
j+c
z
z
z+d
O
O
O
这个数学对象代表什么呢?
显然,如果d为0,那么
o
b
j
e
c
t
object
object就是一个向量,如果d不为0,那么
o
b
j
e
c
t
object
object就是一个向量再加上一个点,也就是一个点。
所以在齐次坐标系下既可以表示向量,又可以表示点。
在(n维)齐次坐标系中,向量的坐标形式为 v = v = v= (a,b,c,0) 表示 v = v = v= a$i + $ b j + j + j+c z z z
在(n维)齐次坐标系中,点的坐标形式为 P = P = P= (a,b,c,d) 表示 v = a d i + b d j + c d z + O v = \frac{a}{d}i + \frac{b}{d}j +\frac{c}{d}z+O v=dai+dbj+dcz+O
我以后还会总结一篇关于齐次坐标系下仿射变换的文章~
欧几里得空间
仿射空间虽然定义了点, 包含了构建几何模型的必要元素, 但是放射空间没有定义长度的概念, 而欧几里得空间引入了这个概念.
包括的数学对象:
- 标量
- 向量
严格来说欧式空间(欧几里得空间)只包括标量好人向量.
引入长度的概念主要是通过定义新的运算.
包含的运算: - 向量-向量加法
- 标量-向量乘法
- (向量-向量)内积(点积)
欧式坐标系
今天不写了,反正三维的欧式坐标系就是你们高中见到的xyz坐标系。
参考:交互式计算机图形学–基于OpenGL着色器得自顶向下方法(第六版)
Coordinate Systems
wiki

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








