排列组合
排列:从n个不同元素中,任取m(m≤n,m与n均为自然数)个元素按照一定的顺序排成一列,称为从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数,称为从n个不同元素中取出m个元素的排列数,用符号 A(n,m)表示。A(n,m)=n(n-1)(n-2)……(n-m+1)=n!/(n-m)!。通常我们所说的排列指的是所有排列的个数,即A(n,m)。
组合:从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。C(n,m)=A(n,m)/m!,C(n,m)=C(n,n-m)。通常我们所说的组合指的是所有组合的个数,即C(n,m)。
组合和排列的区别单从公式来看的话,C(n,m)=A(n,m)/m!,而为什么要除以m!呢?从定义分析,排列是一个有序的序列,也就是将元素x,y放在位置1,2和放在2,1是两个不同的序列,而组合关心的仅仅是是否选取了某个元素,而不考虑顺序,也就是x,y放在位置1,2还是2,1都被认为是相同的组合。由于m个元素在m个位置有m!中排列方式,而这对组合来说只是一种组合,因此需要除以m!。
随机变量
在概率论中,随机变量扮演了重要的角色。千万不要将随机变量和通常所提到的变量相混淆,以为随机变量就是其值具有随机性的变量,而实际上,随机变量是函数,将试验结果映射为实数,更一般地理解为,随机变量是人为定义的基于试验结果的函数,该函数的定义域为试验结果的取值,其值域根据不同情境而不同。通常使用大写字母表示随机变量。
假设随机变量X表示将投掷六面骰子的结果映射为实数,可以定义X将投掷的结果i映射为i,比如投掷的结果为2,则X的结果就为2。还可以定义如果投掷结果为偶数,则X的结果为1,否则为0,这种类型的随机变量被称为指示器变量,用于表示某一事件是否发生。
随机变量X取值a的概率表示为P(X = a) 或P X(a),使用Val(X)表示随机变量的取值范围。
联合分布、边缘分布和条件分布
随机变量的分布指的是取某些值的概率,由定义可知分布本质上是概率,使用P(X)表示随机变量X的分布。当提及多于一个变量的分布时,该分布称为联合分布,因为此时概率由涉及的所有变量共同决定。考虑下面这个联合分布的例子,X为投掷骰子的随机变量,取值为[1,6],Y为抛掷硬币的随机变量,取值为[0,1],二者的联合分布为:
| P | X=1 | X=2 | X=3 | X=4 | X=5 | X=6 |
| Y=0 | 1/12 | 1/12 | 1/12 | 1/12 | 1/12 | 1/12 |
| Y=1 | 1/12 | 1/12 | 1/12 | 1/12 | 1/12 | 1/12 |
使用P(X=a,Y=b)或PX,Y(a,b)表示X取a,Y取b时的概率,使用P(X,Y)表示X,Y的联合分布。给定随机变量X和Y的联合分布,可以定义X或者Y的边缘分布,边缘分布指的是某个随机变量自身的概率分布,为了计算某个随机变量的边缘分布,需要将联合分布中其它随机变量相加,公式为:
条件分布指出了在当其它随机变量已知的情况,某个特定随机变量的分布。而对于某个随机变量X在Y=b的情况下取值为a的条件概率可以定义如下,并可根据该公式确定该变量的条件分布:
可以将上述公式扩展到基于多个随机变量的条件概率,比如,基于两个变量的:
使用符号P(X|Y=b)表示在Y=b的情况下,X的分布。P(X|Y)X分布的集合,其中每个元素为Y取不同值时X的分布。
在概率论中,独立性意味着一个随机变量的分布不受另一个随机变量的影响,使用下面的数学公式定义随即变量X独立于Y:
根据该公式及条件分布的公式可以推导出如果X独立于Y,那么Y也独立于X,推到过程如下:
根据上面的推到过程可以得出P(X,Y)=P(X)P(Y),也就是该公式是X和Y相互独立的等价公式。
更进一步可以定义条件独立,即已知一个或者多个随机变量的值,其余某些变量相互独立则称为条件独立,已知Z,X和Y相互独立的数学定义如下:
最后再看两个重要的定理,分别为链式规则和贝叶斯规则。链式规则的公式如下:
贝叶斯规则的公式如下:
贝叶斯公式通过计算P(Y|X)的值来得到P(X|Y)的值。该公式可以通过条件公式推导而出:
分母的值可通过上面提到的边缘分布计算得出:
sum_z(p(z|d)p(w|z))= p(w|d): 对z进行积分
p(d)p(w|d)p(z|d,w) = p(d,w,z)
=> p(w|d)p(z|d,w) = p(d,w,z)/p(d) = p(w,z|d) = p(z|d)p(w|z)
=> p(z|w,d) = p(z|d)p(w|z) / p(w|d)
离散分布和连续分布
广义上讲,存在两类分布,分别为离散分布和连续分布。离散分布意味着该分布下的随机变量只能取有限的不同值(或者结果空间是有限的)。可以通过简单地枚举随机变量取每个可能值的概率来定义离散分布,这种枚举的方式称为概率质量函数,因为该函数将单位质量(总的概率,1)分割然后分给随机变量可以取的不同值。
连续分布意味着随机变量可以取无穷的不同值(或者结果空间是无穷的),使用概率密度函数(probability density function,PDF)定义连续分布。概率密度函数f为非负的,可积分的函数:
随机变量X的概率根据概率密度函数可得:
特别的,一个连续分布的随机变量的值为任何给定单个值的概率为0,比如连续分布的随机变量X取值为a的概率为0,因为此时积分的上限和下限都为a。
由概率密度函数可引申出累积分布函数,该函数给出了随机变量小于某个值的概率,与概率密度函数的关系为:
因此根据不定积分的含义,
期望值和方差
随机变量的期望值E(X),也称为平均数或者均值,使用下面的公式计算,这两个公式分别用于计算离散随机变量和连续随机变量的期望值:
使用上面的公式计算指示器变量(取值要么为1要么为0的随机变量)可得:
下面是与期望有关的两个重要定理,第一个是期望的线性性质:
无论随机变量是否相互独立,期望的线性性质都成立。而第二个定义只有在随机变量相互独立时才成立:
期望其它重要的性质还有:如果C是常数则E(C)=C,E(CX)=CE(X)。
方差用于衡量一个分布的离散程度,使用下面的公式计算方差:
通常使用
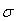

在已知随机变量X的期望时,可以通过下面的公式快速的计算X的方差:
上述推导过程利用了期望的线性性质以及如果C是常数则E(C)=C,E(CX)=CE(X)(此处C为E(X))。方差不是随机变量的线性函数,比如:

如果随机变量X和Y相互独立,那么有下面的关系:

两个随机变量的协方差定义如下,协方差表示两个随机变量的相关程度:
伯努利、泊松和高斯分布
伯努利分布是最基本的分布之一,服从伯努利分布的随机变量X只能取两个值0和1,通常使用p表示X取值为1的概率,即p=P(X=1),q为X取值为0的概率,即q= P(X=0)=1-p。由于X只能取值0和1,因此常用语表示试验是否成功。由定义可知伯努利的分布为:
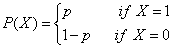
还可以将上面公式概括为: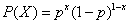
泊松分布是处理事件发生的非常有用的分布,适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数等。
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率,泊松分布的质量函数为:
期望和方差都为λ,计算过程如下:
在上述的推导过程中用到了一个重要的公式:
高斯分布也称为正态分布,是最常使用的分布之一,比如可以在试验次数非常大时用于近似的表示二项式分布,或者在平均发生率很高时近似表示泊松分布,还与大数定理有关。高斯分布由两个参数决定:期望µ和方差σ2,其公式如下:
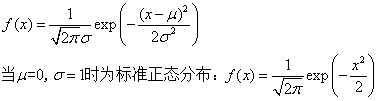
下图为高斯分布的示例图,从该图中可以得知:期望决定正态曲线的中心位置,方差决定正态曲线的陡峭或扁平程度。方差越小,曲线越陡峭;方差越大,曲线越扁平。

在机器学习中经常会处理多变量的高斯分布,k维多变量的高斯分布可以使用参数(µ,Σ)表示,其中µ为期望值的k维向量,Σ为kxk协方差矩阵,其中Σii=Var(Xi),Σij= Cov(X i,X j)。多变量高斯分布的概率密度函数为:









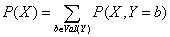
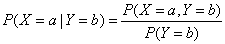
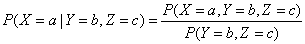
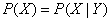
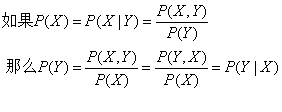
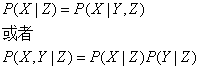
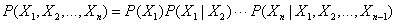
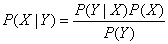
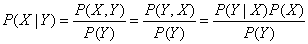
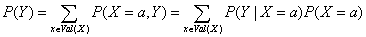
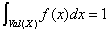

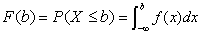


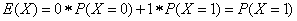

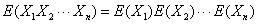
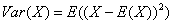
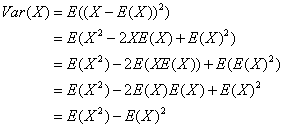
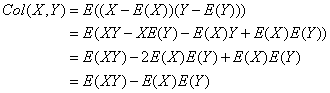
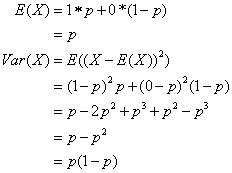
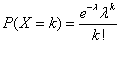
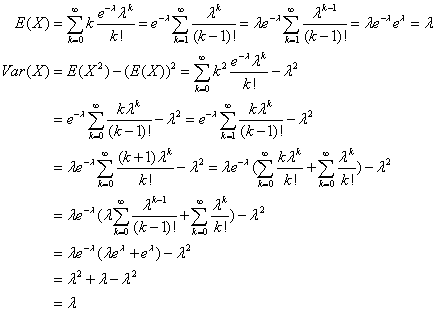

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








