树与搜索

1. 树与树的遍历

树是一种在实际编程中经常遇到的数据结构，它的逻辑结构很简单：除了根节点之外每个节点只有一个父节点，根节点没有父节点；除了叶节点之外所有节点都有一个或者多个子节点，叶节点没有子节点。父节点和子节点之间用指针链接。所谓的二叉树是树的一种特殊结构，在二叉树中每个节点最多只能有两个子节点。二叉树最重要的莫过于遍历，即按照某一顺序访问树中的搜有的节点。通常树有三种遍历方式。

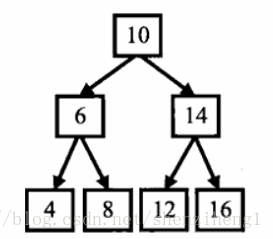
• 前序遍历：根节点-左子节点-右子节点。上图的遍历顺序为：10-6-4-8-14-12-16；
• 中序遍历：左子节点-根节点-右子节点。上图的遍历顺序为：4-6-8-10-12-14-16
• 后序遍历：左子节点-右子节点-根节点。上图的遍历顺序为：4-8-6-12-16-14-10
• 宽度优先遍历：自上到下，自左到右。 上图的遍历顺序为：10-6-14-4-8-12-16

二叉搜索树是二叉树中的一个特例。在二叉搜索树中，左子节点总是小于或者等于根节点，右子节点总是大于等于根节点。上图实际上就是一棵二叉搜索树。可以再平均O(logn)时间内根据数值在二叉搜索树中找到一个节点。

二叉树还有两个特例。分别是堆和红黑树。堆分为最大堆和最小堆。在最大堆中，根节点的值最大，在最小队中，根节点的值最小。很多需要快速查找到最大值最小值的问题都可以通过堆来实现。红黑树是把树中的结点定义为红、黑两种颜色，并通过确定规则使得从根节点到叶节点的最常路径的长度不差偶偶最短路径的二倍。在C++的STL中，set, multiset, map, multimap等数据结构都是结余红黑树实现的。

2.利用前序遍历和中序遍历重建二叉树</