数据结构——搜索树树、B-树、B+树

1.  二叉搜索树

1.1  二叉搜索树的定义

二叉搜索树满足以下几个特性

（1）所有非叶子结点至多拥有两个儿子（Left和Right）

（2）所有结点存储一个关键字

（3）非叶子节点的左/右子树上的任意节点值都小/大于该节点上的值

如：

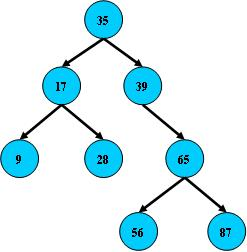
1.2  二叉搜索树的搜索以及性能

二叉搜索树的搜索从根节点开始，如果查询的关键字与结点的值相等则命中；否则比较要查询的关键字和该节点结点值的大小，根据大小进入左/右节点继续搜索；如果左节点或者右节点为空，则找不到相应的关键字。

 

如果二叉搜索树的所有非叶子结点的左右子数的总节点数目差不多（平衡），那么其搜索性能逼近二分查找，它比连续内存空间的二分查找的优点是，改变树的结构（插入与删除结点）不需要移动大段的内存数据。如插入操作：

 

但是由于数据的插入顺序不同，可能会得到不同的二叉搜索树结构，如下：

 

右边也是一个二叉搜索树，但它的搜索性能下降为O(n)了，同样的关键字集合有可能导致不同的树结构索引，所以要尽可能让二叉搜索树保持平衡状态。

 

1.3  AVL树

很明显二叉搜索树最坏的时间复杂度为O(n)，实际使用的二叉搜索树都是在其基础上加上平衡算法，即平衡二叉树（AVL树）。平衡二叉树要求每一个节点的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转将二叉树重新维持在一个平衡状态。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

关于失衡状态包括RR失衡、LL失衡、RL失衡以及LR失衡四种。

 

2.  B-树

2.1  B-树性质

B-tree树即B树，B即Balanced的意思。因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树，其实这是个非常不好的直译，很容易让人产生误解。

AVL树性能较好，但是在处理大量元素的情况是比较费时的。因此B-树出现了。B-树是一种多路搜索树（并不一定是二叉的），对于M阶的B-树有以下定义：

（1）任意非叶子结点最多只有M个儿子，且M>2

（2）根节点的儿子数为[2,M]

（3）除根节点以外的非叶子节点的儿子数为[M/2,M]

（4）每个结点存放至少M/2-1(去上整)和至多M-1个关键字（至少2个关键字）

（5）非叶子结点的关键字个数=指向儿子的指针个数-1

（6）非叶子结点的关键字K[1], K[2], …, K[M-1]满足K[i]< K[i+1]

（7）非叶子结点的指针P[1], P[2], …, P[M]中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树

（8）所有叶子结点位于同一层

如M=3的例子：

 

2.2  B-树的搜索以及特性

B-树的搜索，从根节点开始，对结点内的有序关键字进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点，重复以上过程，直到所对应的儿子指针为空，或已经是叶子结点。

 

B-树的特性总结如下：

（1）关键字集合分布在整颗树中，因此搜索有可能在非叶子结点结束

（2）由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的最少利用率，其最低搜索性能为O(logN)。所以B-树的性能总是等价于二分查找，也就没有平衡的问题。

（3）自动层次控制。由于[M/2,M]的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并。

 

2.3  B-树使用场景

B-树因为最小化了IO次数（因为B类树都是每层节点数目非常多，层数很少），基本上是给硬盘存储定做的。B-树的代码比二叉搜索树复杂的多，但因为IO时间代价很昂贵，所以不惜用更多代码来减少IO。如果是存储内存中的数据，显然选择更容易实现的二叉搜索树。

 

3.  B+树

3.1  B+树性质

B+树是B-树的变体，也是一种多路搜索树。其定义基本与B-树同，除了：

（1）非叶子结点的子树指针与关键字个数相同，而B-树为非叶子结点的子树指针=关键字个数+1

（2）非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1]) （B-树是开区间）的子树

（3）所有关键字都在叶子结点出现

（4）所有叶子结点增加一个链指针，也就是说所有叶子节点连接起来后是个链表

如：（M=3）

 

3.2  B+树的特性

B+的搜索与B-树也基本相同，B+树的特性总结如下：

（1）B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中）。性能等价于一次二分查找

（2）非叶子结点相当于是叶子结点的索引，叶子结点相当于是存储关键字数据的数据层

 

3.3  B+树为什么比B-树更适合于磁盘存储

（1）从Mysql的角度来看，B+树是用来充当索引的，为了减少内存的占用，索引也会被存储在磁盘上。由于B-树的每个节点都有data域（指针），这无疑增大了节点大小，说白了增加了磁盘IO次数（磁盘IO一次读出的数据量大小是固定的，单个数据变大，每次读出的就少，IO次数增多），而B+树除了叶子节点其它节点并不存储数据，也就导致节点小，磁盘IO次数就少。

（2）B+树中数据的串接使得遍历叶子节点非常方便。